专题05 因动点产生的面积问题-版突破中考数学压轴之学霸秘笈大揭秘 学生版+教师版

这是一份专题05 因动点产生的面积问题-版突破中考数学压轴之学霸秘笈大揭秘 学生版+教师版，文件包含专题05圆与三角函数相似结合的综合问题-版突破中考数学压轴之学霸秘笈大揭秘学生版doc、专题05圆与三角函数相似结合的综合问题-版突破中考数学压轴之学霸秘笈大揭秘教师版doc等2份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。

专题5 圆与三角函数、相似结合的综合问题
【典例分析】
例1 如图，AD是△ABC的外接圆⊙O的直径，点P在BC延长线上，且满足∠PAC=∠B．
（1）求证：PA是⊙O的切线；
（2）弦CE⊥AD交AB于点F，若AF•AB=12 ，求AC的长．

思路点拨
（1）先根据直径所对的圆周角是直角和直角三角形的两锐角互余得出∠CAD+∠D=90°，再根据同弧所对的圆周角相等和已知条件等量代换可得∠CAD+∠PAC=90°，根据切线的判定定理即可得出结论；
（2）先判断出∠B=∠ACF，进而判断出△ABC∽△ACF，得出比例式即可得出结论．
满分解答

（2），
，
，[来源:Z&X&X&K]
，
，
，
，
，

，
，
．
例2如图，点C是⊙O直径AB上一点，过C作CD⊥AB交⊙O于点D，连接DA，延长BA至点P，连接DP，使∠PDA＝∠ADC．
（1）求证：PD是⊙O的切线；
（2）若AC＝3，tan∠PDC＝，求BC的长．

思路点拨
（1）求出∠ODA+∠PDA=∠ADC+∠DAO=90°，根据切线的判定得出即可；
（2）求出∠PDC=∠DOC，解直角三角形求出=，设DC=4x，OC=3x，求出3x+3=5x，求出x，即可得出答案．
满分解答
（1）证明：连接OD
∵OD=OA
∴∠ODA=∠OAD
∵CD⊥AB于点C
∴∠OAD+∠ADC=90°
∴∠ODA+∠ADC= 90°
∵∠PDA=∠ADC
∴∠PDA+∠ODA=90°
即∠PDO=90°
∴PD⊥OD
∵D在⊙O上
∴PD是⊙O的切线


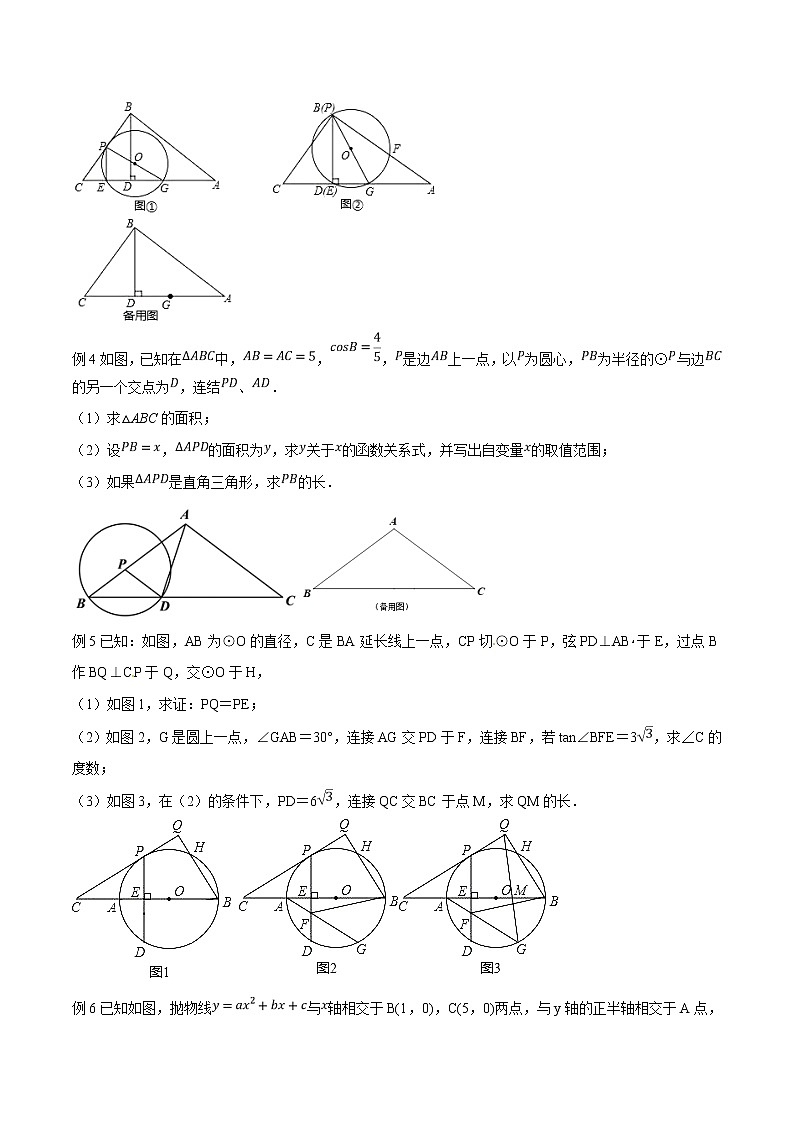
例3已知：如图①，在Rt△ABC中，∠ABC=90°，BD⊥AC于点D，且AB=5，AD=4，在AD上取一点G，使AG=，点P是折线CB﹣BA上一动点，以PG为直径作⊙O交AC于点E，连结PE．
（1）求sinC的值；
（2）当点P与点B重合时如图②所示，⊙O交边AB于点F，求证：∠EPG=∠FPG；
（3）点P在整个运动过程中：
①当BC或AB与⊙O相切时，求所有满足条件的DE长；
②点P以圆心O为旋转中心，顺时针方向旋转90°得到P′，当P′恰好落在AB边上时，求△OPP′与△OGE的面积之比（请直接写出答案）．

思路点拨

（3）①⊙O与AB相切有两种情况，与BC相切有一种情况，如图3、4、5，灵活运用切线的性质，三角函数与勾股定理分别求解即可；
②如图3中，用（2）可知，点P以圆心O为旋转中心，顺时针方向旋转90°得到P，
当P恰好落在AB边上时，此时△OPP′与△OGE的面积之比=××：×××=25：24；
如图6中，当△POH是等腰直角三角形时，连接PE，利用相似三角形的性质求得AE=，PE=，即GE=AE﹣AG=，则△OPP′与△OGE的面积之比=××：×××=25：7.
满分解答

（2）如图2中，连接GF,

在Rt△ABD中，BD==3，
∵BG是直径，
∴∠BFG=∠AFG=90°，
∴sinA=，即，
∴FG=，
∵DG=AD﹣AG=4﹣=，
∴GD=GF，
∴∠EPG=∠FPG；
（3）①如图3中，当⊙O与BC相切时，作OH⊥AB于H，


∴GPC=∠ABC=90°，
∴GP∥AB，
∴∠CGP=∠A，
∴sin∠A=sin∠PGC，
∴，即，
∴PC=，
∴PB=BC﹣PC=，
∴PG==3，
∴OH=PB=，
∴此时⊙O与AB相切，连接PE，
∵PG是⊙O的直径，
∴∠PEG=90°，
∴∠PEC=∠CDB=90°，
∴PE∥BD，
∴DE：CD=PB：BC，
∴DE： =：，
∴DE=；
如图4中，当点P在AB上，⊙O与BC相切时，设切点为T，连接OT，GH，延长TO交GH于N，连接PE，

易证四边形BTNH是矩形，

∴PA=PH+AH=，[来源:Zxxk.Com]
∵PE∥BD，
∴=，即=，
∴AE=，
∴DE=AD﹣AE=4﹣=；
如图5中，当⊙O与AB相切时，GP⊥AB，连接PH，


②如图3中，用（2）可知，点P以圆心O为旋转中心，顺时针方向旋转90°得到P，
当P恰好落在AB边上时，
此时△OPP′与△OGE的面积之比=××：×××=25：24；
如图6中，当△POH是等腰直角三角形时，满足条件；
连接PE，

∵PH=GH=，AH=2，
∴PA=，OP=OH=，
∵PE∥BD，
∴PA：AB=AE：AD=PE：BD，
∴：5=AE：4=PE：3，
∴AE=，PE=，[来源:ZXXK]
∴GE=AE﹣AG=，
∴△OPP′与△OGE的面积之比=××：×××=25：7；
综上所述，满足条件的△OPP′与△OGE的面积之比为25：24或25：7．
例4如图，已知在中，，，是边上一点，以为圆心，为半径的⊙与边的另一个交点为，连结、．
（1）求△ABC的面积；
（2）设，的面积为，求关于的函数关系式，并写出自变量的取值范围；
（3）如果是直角三角形，求的长．

思路点拨
(1)分别求出BC和BC上的高；(2)作DM⊥AB垂足为M，用含x的式子表示出AP和DM；(3)分∠ADP＝90°和∠PAD＝90°两种情况求解.
满分解答

(2)如图，作DM⊥AB垂足为M，


(3)∠APD＜90°，
过C作CE⊥AB交BA的延长线于E，可得cos∠CAE＝.
①当∠ADP＝90°时，
cos∠APD＝cos∠CAE＝，则，解得x＝；
②当∠PAD＝90°时，，解得x＝.
所以PB的值为或.

例5已知：如图，AB为⊙O的直径，C是BA延长线上一点，CP切⊙O于P，弦PD⊥AB于E，过点B作BQ⊥CP于Q，交⊙O于H，
（1）如图1，求证：PQ＝PE；
（2）如图2，G是圆上一点，∠GAB＝30°，连接AG交PD于F，连接BF，若tan∠BFE＝3，求∠C的度数；
（3）如图3，在（2）的条件下，PD＝6，连接QC交BC于点M，求QM的长．

思路点拨
（1）连接OP，PB，由已知易证∠OBP=∠OPB=∠QBP，从而可得BP平分∠OBQ，结合BQ⊥CP于点Q，PE⊥AB于点E即可由角平分线的性质得到PQ=PE；
（2）如下图2，连接OP，则由已知易得∠CPO=∠PEC=90°，由此可得∠C=∠OPE，设EF=x，则由∠GAB=30°，∠AEF=90°可得AE=，在Rt△BEF中，由tan∠BFE=可得BE=，从而可得AB=，则OP=OA=，结合AE=可得OE=，这样即可得到sin∠OPE=，由此可得∠OPE=30°，则∠C=30°；

满分解答
（1）如下图1，连接OP，PB，∵CP切⊙O于P，
∴OP⊥CP于点P，
又∵BQ⊥CP于点Q，
∴OP∥BQ，
∴∠OPB=∠QBP，
∵OP=OB，
∴∠OPB=∠OBP，
∴∠QBP=∠OBP，
又∵PE⊥AB于点E，
∴PQ=PE；


在Rt中,tan∠BFE=3
∴
∴
∴
∴
∴在RtPEO中,
∴30°；


∴在Rt中， ，
∴，
∴QB=9，
在△ABG中，AB为⊙O的直径，
∴AGB=90°，
∵BAG=30°，
∴BG=6，ABG=60°，
过点G作GN⊥QB交QB的延长线于点N，则∠N=90°，∠GBN=180°-∠CBQ-∠ABG=60°，
∴BN=BQ·cos∠GBQ=3，GN=BQ·sin∠GBQ=，
∴QN=QB+BN=12，
∴在Rt△QGN中，QG=，
∵∠ABG=∠CBQ=60°，
∴BM是△BQG的角平分线，
∴QM：GM=QB：GB=9：6，
∴QM=.

点睛：解本题第3小题的要点是：（1）作出如图所示的辅助线，结合已知条件和（2）先求得BQ、BG的长及∠CBQ=∠ABG=60°；（2）再过点G作GN⊥QB并交QB的延长线于点N，解出BN和GN的长，这样即可在Rt△QGN中求得QG的长，最后在△BQG中“由角平分线分线段成比例定理”即可列出比例式求得QM的长了.
例6已知如图，抛物线与轴相交于B(1，0)，C(5，0)两点，与y轴的正半轴相交于A点，过A，B，C三点的⊙P与y轴相切于点A，M为轴负半轴上的一个动点，直线MB交抛物线于N，交⊙P于D．
(1)填空:A点坐标是____，⊙P半径的长是_______，=____，=____，=____；
(2)若S△BNC:S△AOB＝48:5，求N点的坐标；
(3)若△AOB与以A，B，D为顶点的三角形相似，求MB·MD的值．

思路点拨
（1）先将B、C两点坐标代入抛物线方程，再根据题意求得⊙P半径，进而求得抛物线方程；
（2）根据S△BNC：S△AOB=48：5求出N点的y坐标，将yN代入抛物线方程即可求得N点坐标；
（3）根据三角形相似的性质和射影定理便可求得MB•MD的值．
满分解答
（1）⊙P的半径=3,=,=,=；

（3）过点A作直径AQ联接BQ，

∴∠ABQ=90º,∠BAO+∠AOB=90º,
∵MA与⊙P相切于点A，∴∠OAB+∠BAO=90º,
∴∠OAB=∠AOB,而∠AQB=∠ADB,
∴∠OAB=∠ADB,而∠AMB=AMD,
∴△MAB∽△MDA,
∴,∴…
ⅰ当△AOB∽△DBA时，∠ABD=∠AOB=90º,

易证△AOB∽△BOM,则
∴OM=,,
∴;
ⅱ当△AOB∽△DAB时，∠BAD=∠AOB=90º,


【变式训练】
1．如图，直线l1∥l2，⊙O与l1和l2分别相切于点A和点B．点M和点N分别是l1和l2上的动点，MN沿l1和l2平移．⊙O的半径为1，∠1=60°．有下列结论：①MN=；②若MN与⊙O相切，则AM=；③若∠MON=90°，则MN与⊙O相切；④l1和l2的距离为2，其中正确的有（　　）

A．4个 B．3个 C．2个 D．1个
【答案】B
【解析】
【分析】
首先过点N作NC⊥AM于点C，直线l1∥l2，⊙O与l1和l2分别相切于点A和点B，⊙O的半径为1，易求得MN==，l1和l2的距离为2；若∠MON=90°，连接NO并延长交MA于点C，易证得CO=NO，继而可得即O到MN的距离等于半径，可证得MN与⊙O相切；由题意可求得若MN与⊙O相切，则AM=或．
【详解】
如图1，


如图3，

若∠MON=90°，连接NO并延长交MA于点C，则△AOC≌△BON，
故CO=NO，△MON≌△MOM′，故MN上的高为1，即O到MN的距离等于半径．故③正确；
如图2，


2．如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为上的动点，点M，N，P分别是AD，DC，CB的中点．若⊙O的半径为2，则PN+MN的长度的最大值是（　　）

A．　　　B．　　　C．　　　D．
【答案】D
【解析】
【分析】
连接OC、OA、BD，作OH⊥AC于H．首先求出AC的长，利用三角形的中位线定理即可解决问题.
【详解】
解：连接OC、OA、BD，作OH⊥AC于H．


【点睛】
本题考查圆周角定理、三角形的中位线的定理、解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
3．如图，AB是⊙O的直径，CD是⊙O的切线，切点为D，CD与AB的延长线交于点C，∠A＝30°，CD＝3，则AB的值是（　　）

A．3 B． C．6 D．
【答案】B
【解析】
【分析】
连接OD，由圆周角定理可得∠DOC＝60°，根据三角函数可求OD的长，即可求AB的长．
【详解】
连接OD，


【点睛】
本题考查了切线的性质，圆周角定理，解直角三角形，熟练运用这些性质进行推理是解本题的关键．
4．如图，已知AD＝30，点B，C是AD的三等分点，分别以AB、BC、CD为直径作圆，圆心分别为E、F、G，AP切⊙G于点P，交⊙F于M、N，则弦MN的长是________．

【答案】8
【解析】
【分析】[来源:Z§X§X§K]
连接PG、MF，过F作FQ⊥MN于点Q，根据AP是⊙G的切线，可证明△AFQ∽△AGP，利用相似比，可求得FQ=3，连接FM，在直角△FQM中根据勾股定理得到MQ=4，则MN=8．
【详解】


∴FQ=PG=3，
在直角△FQM中，MQ=
==4，
则MN=2MQ=8．
故答案为：8
【点睛】
本题主要考查切线的性质定理，切线垂直于过切点的半径，并且本题还考查了相似三角形的性质，对应边的比相等．
5．如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=5，BC=10，连接AC、BD，以BD为直径的圆交AC于点E．若DE=3，则AD的长为________.

【答案】2
【解析】
【分析】
先证明△ADF∽△CAB，利用相似三角形的性质可得.再证明△DEF∽△DBA，利用相似三角形的性质可得，据此可求出DF的值，进而求出AD的值.
【详解】
如图所示，过点D作DF⊥AC于点F，


在Rt△ABD中，.
∵同弧所对的圆周角相等，
∴∠DEF=∠DBA，
又∵∠DFE=∠DAB=90°，
∴△DEF∽△DBA，
∴，即，
∴DF=2，
∴AD=2.
故答案为：2.
【点睛】
本题主要了平行线的性质、勾股定理、圆周角定理以及相似三角形的判定与性质.熟练掌握相似三角形的判定与性质是解答本题的关键.
6．如图，五边形是边长为的正五边形，是正五边形的外接圆，过点作的切线，与、的延长线交分别于点和，延长、相交于点，那么的长度是________．

【答案】
【解析】
【分析】
先证明AG=AF，由SSS得到△OHD与△OED全等，得出∠ODH=∠ODE=54°，证出∠B=∠C=72°，设GB=xcm，由△DHB∽△GBD，利用相似三角形对应边成比例列出比例式，求出x的值，即可得出结果．
【详解】

连接DG，如图所示：

∵BC是⊙O的切线，
∴OD⊥BC，
∴∠BFO=∠CFO=90°，
在△OHD与△OED中，，
∴△OHD≌△OED（SSS），
∴∠ODH=∠ODE=54°，
∴∠HDB=∠EDC=36°，
∴∠B=∠C=72°，
∴BD=DH=DE=DC=GF，
∴GF=BC，

设GB=x，
∵∠BDH=∠BGD，∠B=∠B，
∴△DHB∽△GBD，
∴，即，
整理得：x2-2x-4=0，
解得：x=1±（负值舍去），
∴AG=GB=1+，
∴AB=2+2；
故答案为：2+2．
【点睛】
本题考查了正五边形的性质，全等三角形的判定与性质，相似三角形的判定与性质，等腰三角形的判定，切线的性质；熟练掌握正五边形的性质，证明三角形全等和三角形相似是解题的关键．
7．如图，已知在⊙O中，直径AB＝4，点E是OA上任意一点，过E作弦CD⊥AB，点F是上一点，连接AF交CE于点H，连接AC，CF，BD，OD.

(1)求证：△ACH∽△AFC；
(2)猜想：AH·AF与AE·AB的数量关系，并证明你的猜想；
(3)探究：当点E位于何处时，S△AEC∶S△BOD＝1∶4？并加以说明．
【答案】（1）详见解析；（2）AH·AF＝AE·AB，证明详见解析；（3）当OE＝ (或AE＝)时，S△AEC∶S△BOD＝1∶4.
【解析】
【分析】
（1）根据垂径定理得到弧AC=弧AD，再根据圆周角定理的推论得到∠F=∠ACH，根据两个角对应相等证明两个三角形相似；
（2）连接BF，构造直角三角形，把要探索的四条线段放到两个三角形中，根据相似三角形的判定和性质证明；
（3）根据三角形的面积公式，得到两个三角形的面积比即为AE：OB，进一步转化为AE：AO的比，再根据半径的长求得OE的长．
【详解】

(3)解：当OE＝ (或AE＝)时，S△AEC∶S△BOD＝1∶4.∵直线AB⊥CD，∴CE＝ED，又∵S△AEC＝AE·CE，S△BOD＝OB·ED，∴＝＝，∵⊙O的半径为2，∴＝，∴OE＝.
【点睛】
能够综合运用垂径定理和圆周角定理的推论得到有关的角相等．掌握相似三角形的判定和性质．
8．如图，是的直径，是上一点，，

（1）求证：是的切线；
（2）若，，求的长.
【答案】（1）详见解析；（2）2
【解析】
【分析】
（1）连接OC，由AB是直径可得∠ACB=90°，由OA=OC可得∠BAC=OCA，根据∠ACD=∠B，∠B+∠BAC=90°，通过等量代换可得∠OCD=90°，即可得答案；根据∠ACD=∠B，∠BAC=∠ADC=90°，可证明△ABC∽△ACD，根据相似三角形的性质即可求出AC的长.
【详解】

∴
∴
∴是的切线；


【点睛】
本题考查圆周角定理，切线的判定及相似三角形的判定与性质，熟练掌握相关定理及性质是解题关键.
9．如图所示，△ABC内接于⊙O，AC是⊙O的直径，点D是劣弧AB的中点，过点D作直线BC的垂线，分别交CB，CA的延长线于E，F两点．
(1)求证：EF是⊙O的切线；
(2)若EF＝8，EC＝6，求⊙O的半径．

【答案】（1）证明见解析；（2）.
【解析】
【分析】
（1）连接OD交AB于点G，依据垂径定理的推论可以得出OD⊥AB，结合题意易得AB∥EF，进而不难得到OD⊥EF，即可证明结论；
（2）先根据勾股定理求出CF的长，由（1）知OD∥CE，然后利用平行线分线段成比例列式求解即可求出⊙O的半径.
【详解】
(1)证明：连结OD，
∵D是的中点，
∴OD⊥AB.
又∵AC为⊙O的直径，
∴BC⊥AB，∴OD∥CE.
又∵CE⊥EF，∴OD⊥EF，
即EF是⊙O的切线．


【点睛】
本题主要考查了切线的判定，圆周角定理的推论，垂径定理定理的推论，平行线分线段成比例定理.证明一条直线是圆的切线常用的方法有：①若图形中已给出直线与圆的公共点，但未给出过点的半径，则可先连结过此点的半径，再证其与直线垂直；②若图形中未给出直线与圆的公共点，则需先过圆心作该直线的垂线，再证垂足到圆心的距离等于半径.
10．如图，AB是⊙O的直径，C为⊙O上一点，经过点C的直线与AB的延长线交于点D，连接AC，BC，∠BCD＝∠CAB．E是⊙O上一点，弧CB＝弧CE，连接AE并延长与DC的延长线交于点F．
（1）求证：DC是⊙O的切线；
（2）若⊙O的半径为3，sin∠D＝，求线段AF的长．

【答案】(1)见解析；（2）.
【解析】
【分析】
（1）连接OC，BC，由AB是⊙O的直径，得到∠ACB=90°，即∠1+∠3=90°．根据等腰三角形的性质得到∠1=∠2．得到∠DCB+∠3=90°．于是得到结论；
（2）根据三角函数的定义得到OD=5，AD=8．根据弧CB＝弧CE得到∠2=∠4．推出OC∥AF．根据相似三角形的性质即可得到结论．
【详解】


（2）解：在Rt△OCD中，OC＝3，sinD＝．
∴OD＝5，AD＝8．
∵弧CB＝弧CE，
∴∠2＝∠4．
∴∠1＝∠4．
∴OC∥AF．
∴△DOC∽△DAF．
∴=．
∴AF＝．
【点睛】
本题考查了切线的判定，圆周角定理，解直角三角形，三角形的性质与判定，正确的作出辅助线是解题的关键．
11．如图，AB是半圆O的直径，点P在BA的延长线上，PD切⊙O于点C，BD⊥PD，垂足为D，连接BC.
(1)求证：BC平分∠PBD；
(2)求证：PC2＝PA·PB；
(3)若PA＝2，PC＝2，求阴影部分的面积(结果保留π).

【答案】（1）证明见解析；（2）证明见解析；（3）S阴影＝2－π.
【解析】
【分析】
（1）连接OC，由PD切⊙O于点C，得到OC⊥PD，根据平行线的性质得到∠DBC=∠BCO，根据的预计实现的性质得到∠OCB=∠OBC，等量代换得到∠OBC=∠CBD，于是得到即可；
（2）连接AC，由AB是半圆O的直径，得到∠ACB=90°，推出∠ACP=∠ABC，根据相似三角形的性质即可得到结论；
（3）根据图形的面积公式即可得到结果．
【详解】
（1）连接OC，

∵PD切⊙O于点C，
∴OC⊥PD，
∵BD⊥PD，
∴BD∥OC，
∴∠DBC＝∠BCO，
∵OC＝OB，
∴∠OCB＝∠OBC，
∴∠OBC＝∠CBD，
∴BC平分∠PBD；

（3）∵PC2＝PA·PB，PA＝2，PC＝2，
∴PB＝6，
∴AB＝4，
∴OC＝2，PO＝4，
∴∠POC＝60°，
∴S阴影＝S△POC－S扇形＝×2×2－＝2－π.
【点睛】
本题考查了相似三角形的判定和性质，等腰三角形的性质，平行线的性质，角平分线的定义，扇形面积的计算，熟练掌握相似三角形的判定和性质是解题的关键．
12．如图，AB 为⊙O 的直径，C 为⊙O 上一点，AD⊥CE 于点 D，AC 平分∠DAB．
（1）求证：直线 CE 是⊙O 的切线；
（2）若 AB＝10，CD＝4，求 BC 的长．

【答案】（1）证明见解析；（2）BC＝2或4．
【解析】
【分析】
(1)如图，连接OC，由AC平分∠DAB得到∠DAC=∠CAB，然后利用等腰三角形的性质得到∠OCA=∠CAB，接着利用平行线的判定得到AD∥CO，而CD⊥AD，由此得到CD⊥AD，最后利用切线的判定定理即可证明CD为⊙O的切线；
(2)证明△DAC∽△CAB，根据相似三角形对应边成比例进行求解即可.
【详解】

∴AD∥CO，
∵CD⊥AD，
∴OC⊥CD，
∵OC是⊙O直径且C在半径外端，
∴CD为⊙O的切线；


【点睛】
本题考查了切线的判定、圆周角定理、相似三角形的判定与性质等，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.
13．如图，在⊙O中，AB是⊙O的直径，AE是弦，OG⊥AE于点G，交⊙O 于点D，连结BD交AE于点F，延长AE至点C，连结BC．
(1)当BC=FC时，证明：BC是⊙O的切线；
(2)已知⊙O的半径，当tanA=，求GF的长．

【答案】（1）见解析；（2）1
【解析】
【分析】
（1）由OD⊥AE可知∠D+∠GFD=90°，由等腰三角形的性质可得∠BFC=∠FBC，∠OBD=∠D，从而可证∠OBC=90°；
(2) 连接 BE，在Rt△AOG中，可求出OG= 3， AG=4，由垂径定理得GE= AG=4，然后通过证明△FGD∽△FEB，可求出GF的长.
【详解】

(2) 连接 BE，

∵⊙O半径，tanA=，
∴sinA=,cosA=．
∴在Rt△AOG中，OG=OA× sinA=5×=3， AG=OA× cosA=5×=4=GE．

【点睛】
本题考查了等腰三角形的性质，切线的判定，解直角三角形，三角形的中位线，相似三角形的判定与性质.熟记切线的判定定理是解（1）的关键，证明△FGD∽△FEB是解（2）的关键.
14．如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，弦PB与CD交于点F，且FC＝FB．
（1）求证：PD∥CB；
（2）若AB＝26，EB＝8，求CD的长度．

【答案】（1）证明见解析；（2）CD＝24．
【解析】
【分析】
（1）欲证明PD∥BC，只要证明∠P＝∠CBF即可；
（2）由△ACE∽△CBE，可得，求出EC，再根据垂径定理即可解决问题.
【详解】

（2）连接AC，

∵AB是直径，
∴∠ACB＝90°，
∵AB⊥CD，
∴CE＝ED，∠AEC＝∠CEB＝90°，
∵∠CAE+∠ACE＝90°，∠ACE+∠BCE＝90°，
∴∠CAE＝∠BCE，
∴△ACE∽△CBE，
∴，
∴，
∴EC2＝144，
∵EC＞0，
∴EC＝12，
∴CD＝2EC＝24．
【点睛】
本题考查圆周角定理，垂径定理，平行线的判定，等腰三角形的性质，相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．
15．如图⊙O的内接△ABC中，外角∠ACF的角平分线与⊙O相交于D点，DP⊥AC，垂足为P，DH⊥BF，垂足为H.问：
(1)∠PDC与∠HDC是否相等，为什么？
(2)图中有哪几组相等的线段？
(3)当△ABC满足什么条件时，△CPD∽△CBA，为什么？

【答案】（1）相等，理由详见解析；（2）PC＝HC，DP＝DH，AP＝BH，AD＝BD；（3）∠ABC＝90°且∠ACB＝60°时，△CPD∽△CBA.
【解析】
【分析】
（1）根据“AAS”证明△CDH≌△CDP即可； 
（2）发现全等三角形，根据全等三角形的对应边相等证明出线段相等；
（3）根据其中一个是直角三角形得到AC必须是直径．再根据另一对角对应相等，结合利用平角发现∠PCD＝∠DCF＝∠ACB=60°才可．
【详解】

又∵CD=CD，
∴△CDH≌△CDP，
∴∠PDC＝∠HDC.
(2) ∵△CDH≌△CDP，
∴PC＝HC，DP＝DH，
∵∠DAP=∠DBH，∠APD=∠BHD=90°，
∴△ADP≌△BDH，
∴AP＝BH，AD＝BD.
综上可得：PC＝HC，DP＝DH，AP＝BH，AD＝BD.

【点睛】
本题考查了角平分线的定义，垂线的定义，全等三角形的判定与性质，相似三角形的性质，圆周角定理的推论等知识.掌握全等三角形的判定和性质，能够根据已知的三角形的形状探索若相似应满足的条件是解答本题的关键．
16．如图,AB是⊙O的直径, ⊙O过BC的中点D,DE⊥AC.求证: △BDA∽△CED.

【答案】证明见解析.
【解析】
【分析】
不难看出△BDA和△CED都是直角三角形，证明△BDA∽△CED，只需要另外找一对角相等即可，由于AD是△ABC的中线，又可证AD⊥BC，即AD为BC边的中垂线，从而得到∠B=∠C，即可证相似．
【详解】

【点睛】
本题重点考查了圆周角定理、直径所对的圆周角为直角及相似三角形判定等知识的综合运用．
17．如图，在△ABC中，AB＝AC，以AB为直径作半圆⊙O，交BC于点D，连接AD．过点D作DE⊥AC，垂足为点E．
（1）求证：DE是⊙O的切线；
（2）当⊙O半径为3，CE＝2时，求BD长．

【答案】（1）证明见解析；（2）BD＝2．
【解析】
【分析】
（1）连接OD，AB为⊙0的直径得∠ADB=90°，由AB=AC，根据等腰三角形性质得AD平分BC，即DB=DC，则OD为△ABC的中位线，所以OD∥AC，而DE⊥AC，则OD⊥DE，然后根据切线的判定方法即可得到结论；
（2）由∠B=∠C，∠CED=∠BDA=90°，得出△DEC∽△ADB，得出，从而求得BD•CD=AB•CE，由BD=CD，即可求得BD2=AB•CE，然后代入数据即可得到结果．
【详解】
（1）证明：连接OD，如图，

∵AB为⊙0的直径，
∴∠ADB＝90°，
∴AD⊥BC，
∵AB＝AC，
∴AD平分BC，即DB＝DC，
∵OA＝OB，
∴OD为△ABC的中位线，
∴OD∥AC，
∵DE⊥AC，
∴OD⊥DE，
∴DE是⊙0的切线；

【点睛】
本题考查了切线的判定定理：过半径的外端点且与半径垂直的直线为圆的切线．也考查了等腰三角形的性质、三角形相似的判定和性质．
18．如图，为的直径，，为上一点，且AC=BC，为BC上的一动点，延长至，使得，连接．
（1）求证：直线是的切线；
（2）若点由点运动到点，则线段扫过的面积是__________．（结果保留）

【答案】（1）见解析；（2）
【解析】
【分析】
（1）做辅助线根据证明,由相似三角形性质即可解题,（2）作出图像得S阴影=S△ABQ-S△AOC-S扇形BOC,即可解题.
【详解】
（1）证明：连接．


，即．
是的直径，
直线是的切线．[来源:ZXXK]


【点睛】
本题考查了三角形的相似,切线的证明,不规则图形求面积,中等难度,证明切线是解题关键.
19．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，经过点A作AE⊥OC，垂足为点D，AE与BC交于点F，与过点B的直线交于点E，且EB＝EF．
（1）求证：BE是⊙O的切线；
（2）若CD＝1，cos∠AEB＝，求BE的长．

【答案】（1）见解析；（2）BE＝
【解析】
【分析】
（1）由OB＝OC可得∠OBC＝∠OCB，由EB＝EF可知∠EBC＝∠EFB，根据∠AFC+∠OCB＝90°可知∠EBC+∠OBC＝90°，即可得结论；
（2）由（1）可知∠AEB+∠EAB＝90°，由∠AOD+∠EAB＝90°即可证明∠AOD＝∠AEB，设⊙O的半径为r，根据cos∠AOD＝cos∠AEB＝可求出r的值，即可得AB的值，根据cos∠AEB＝＝可得AE＝BE，利用勾股定理求出BE的长即可.
【详解】

（2）设⊙O的半径为r，则OA＝OC＝r，
又CD＝1，
∴OD＝r﹣1，
∵∠AOD+∠EAB＝90°，∠AEB+∠EAB＝90°，
∴∠AOD＝∠AEB，
∴cos∠AOD＝cos∠AEB＝，
∴在Rt△AOD中，cos∠AOD＝＝，即＝，
解得：r＝，
∵AB是⊙O的直径，
∴AB＝5，
在Rt△AEB中，cos∠AEB＝＝，
∴AE＝BE，
又AE2＝AB2+BE2，即（BE）2＝BE2+52，
解得：BE＝．
20．如图，已知Rt△ACE中，∠AEC=90°，CB平分∠ACE交AE于点B，AC边上一点O，⊙O经过点B、C，与AC交于点D，与CE交于点F，连结BF。
（1）求证：AE是⊙O的切线；
（2）若，AE=8，求⊙O的半径；
（3）在(2)条件下，求BF的长。

【答案】（1）证明见解析 （2） （3）
【解析】
【分析】
(1) 连接OB,根据OB=OC得出∠1=∠2，再根据CB平分∠ACE，得出∠2=∠3，再利用平行线的性质求解即可;(2) 连接DF,根据同弧所对圆周角相等得出∠CDF=∠CBF，再利用直径所对的圆周角为90°，得出∠DFC=90°，由OB//CE，得出△AOB∽△ACE，利用相似三角形的性质，列出方程求解即可;(3) 先证出△ACB∽△BCF，再利用相似三角形的性质得出=，进而求出结果.
【详解】
（1）证明：如图1，连接OB，
∵OB=OC，∴∠1=∠2，
∵CB平分∠ACE，∴∠2=∠3，
∴∠1=∠3，∴OB∥CE，
∴∠ABO=∠AEC=90°，即OB丄AE，
∴AE是⊙0的切线；

（3）在Rt△AOB中AO=10-=，cos A=，
∴AB=5，
在Rt△DCF中CD=，cos∠CDF=cos∠CBF=，
∴CF=，
∵∠A=∠CBF，∠2=∠3，
∴△ACB∽△BCF，
∴=，
∴，
解得，BC=，BF=.