2020届全国各地高考试题分类汇编05统计概率
展开复数5
逻辑用语8
函数与导数10
三角函数和解三角形34
平面向量47
07 数列53
不等式和线性规划69
空间立体几何73
平面解析几何98
\l "_TOC_250000" 统计和概率123
不等式选讲142
1.(2020•北京卷)在(
11 统计和概率
x
2)5 的展开式中, x2 的系数为().
5
5C.
10
D. 10
【答案】C
【解析】首先写出展开式的通项公式,然后结合通项公式确定 x2 的系数即可.
x
【详解】
2
5
展开式的通项公式为: T
Cr
x 2
2
5r
Cr x 2 ,
5rrr
r 155
令 5 r 2 可得: r 1 ,则 x2 的系数为: 21 C1 2 5 10 .故选:C.
25
【点睛】二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根据所给出的条件(特定项) 和通项公式,建立方程来确定指数(求解时要注意二项式系数中 n 和 r 的隐含条件,即 n,r 均为非负整数,
男生
女生
支持
不支持
支持
不支持
方案一
200 人
400 人
300 人
100 人
方案二
350 人
250 人
150 人
250 人
且 n≥r,如常数项指数为零、有理项指数为整数等);第二步是根据所求的指数,再求所求解的项. 2.(2020•北京卷)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案:方案一、方案二.为了 解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如下表:
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取 2 人,全体女生中随机抽取 1 人,估计这 3 人中恰有 2 人支持方案一的概率;
(Ⅲ)将该校学生支持方案的概率估计值记为 p0 ,假设该校年级有 500 名男生和 300 名女生,除一年级外其他年级学生支持方案二的概率估计值记为 p1 ,试比较 p0 与 p1 的大小.(结论不要求证明)
1
【答案】(Ⅰ)该校男生支持方案一的概率为
3
3
,该校女生支持方案一的概率为;
4
(Ⅱ) 13 ,(Ⅲ) p p
3610
【解析】(Ⅰ)根据频率估计概率,即得结果;
(Ⅱ)先分类,再根据独立事件概率乘法公式以及分类计数加法公式求结果;
(Ⅲ)先求 p0 ,再根据频率估计概率 p1 ,即得大小.
2001
【详解】(Ⅰ)该校男生支持方案一的概率为,
200+4003
3003
该校女生支持方案一的概率为;
300+1004
(Ⅱ)3 人中恰有 2 人支持方案一分两种情况,(1)仅有两个男生支持方案一,(2)仅有一个男生支持方案
一,一个女生支持方案一,
1 23
1 11 313
所以 3 人中恰有 2 人支持方案一概率为: (3) (1 4) C2 (3)(1 3) 4 36 ;
(Ⅲ) p1 p0
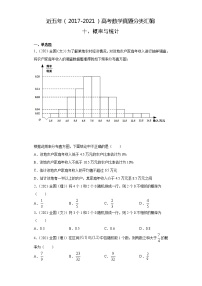
【点睛】本题考查利用频率估计概率、独立事件概率乘法公式,考查基本分析求解能力,属基础题. 3.(2020•全国 1 卷)某校一个课外学习小组为研究某作物种子的发芽率 y 和温度 x(单位:°C)的关系, 在 20 个不同的温度条件下进行种子发芽实验,由实验数据(xi , yi )(i 1, 2,, 20) 得到下面的散点图:
由此散点图,在 10°C 至 40°C 之间,下面四个回归方程类型中最适宜作为发芽率 y 和温度 x 的回归方程类
型的是()
y a bx
y a bx2
y a bex
y a b ln x
【答案】D
【解析】根据散点图的分布可选择合适的函数模型.
【详解】由散点图分布可知,散点图分布在一个对数函数的图象附近,
因此,最适合作为发芽率 y 和温度 x 的回归方程类型的是 y a b ln x .故选:D.
【点睛】本题考查函数模型的选择,主要观察散点图的分布,属于基础题.
y25
4.(2020•全国 1 卷) (x
)(x y)
x
的展开式中 x3y3 的系数为()
A. 5B. 10
C. 15D. 20
【答案】C
5
r 5r r
y2
x 5
【解析】求得(x y) 展开式的通项公式为Tr 1 C5 xy ( r N 且 r 5 ),即可求得x 与(x y)
展开式的乘积为Cr x6r yr 或Cr x4r yr 2 形式,对 r 分别赋值为 3,1 即可求得 x3 y3 的系数,问题得解.
55
【详解】(x y)5 展开式的通项公式为T
Cr x5r yr ( r N 且 r 5 )
y2
x
r 15
5
所以x 的各项与(x y) 展开式的通项的乘积可表示为:
xT xCr x5r yr Cr x6r yry2
y2r
5r rr
4r r 2
r 155
和 x Tr 1
x C5 xy
C5 xy
在 xT Cr x6r yr 中,令 r 3,可得: xT C3 x3 y3 ,该项中 x3 y3 的系数为10 ,
r 1545
y2r
4r r 2
y21 3 33 3
在 x Tr 1 C5 xy
中,令 r 1 ,可得:
x T2 C5 x y
,该项中 x y 的系数为5
所以 x3 y3 的系数为10 5 15 .故选:C
【点睛】本题主要考查了二项式定理及其展开式的通项公式,还考查了赋值法、转化能力及分析能力,属 于中档题.
5.(2020•全国 1 卷)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一场轮空,直
至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛
1
结束.经抽签,甲、乙首先比赛,丙轮空.设每场比赛双方获胜的概率都为,
2
求甲连胜四场的概率;
求需要进行第五场比赛的概率;
求丙最终获胜的概率.
1
【答案】(1)
16
3
;(2)
4
7
;(3).
16
【解析】(1)根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率;
计算出四局以内结束比赛的概率,然后利用对立事件的概率公式可求得所求事件的概率;
列举出甲赢的基本事件,结合独立事件的概率乘法公式计算出甲赢的概率,由对称性可知乙赢的概率 和甲赢的概率相等,再利用对立事件的概率可求得丙赢的概率.
【详解】(1)记事件 M :甲连胜四场,则 P M 2
1 4
1 ;
16
记事件 A 为甲输,事件 B 为乙输,事件C 为丙输, 则四局内结束比赛的概率为
1
1
4
P P ABAB P ACAC P BCBC P BABA 4 2 4 ,
所以,需要进行第五场比赛的概率为 P 1 P 3 ;
4
记事件 A 为甲输,事件 B 为乙输,事件C 为丙输,
记事件 M :甲赢,记事件 N : 丙赢,则甲赢的基本事件包括: BCBC 、 ABCBC 、 ACBCB 、
BABCC 、 BACBC 、 BCACB 、 BCABC 、 BCBAC ,
1
4
所以,甲赢的概率为 P M 2
1 5
7 2
9 .
32
由对称性可知,乙赢的概率和甲赢的概率相等,所以丙赢的概率为 P N 1 2 9 7 .
3216
【点睛】本题考查独立事件概率的计算,解答的关键就是列举出符合条件的基本事件,考查计算能力,属 于中等题.
6.(2020•全国 2 卷)在新冠肺炎疫情防控期间,某超市开通网上销售业务,每天能完成 1200 份订单的配货, 由于订单量大幅增加,导致订单积压.为解决困难,许多志愿者踊跃报名参加配货工作.已知该超市某日积压500 份订单未配货,预计第二天的新订单超过 1600 份的概率为 0.05,志愿者每人每天能完成 50 份订单的配货,为使第二天完成积压订单及当日订单的配货的概率不小于 0.95,则至少需要志愿者()
A. 10 名B. 18 名C. 24 名D. 32 名
【答案】B
【解析】算出第二天订单数,除以志愿者每天能完成的订单配货数即可.
【详解】由题意,第二天新增订单数为500 1600 1200 900 ,设需要志愿者 x 名,
50x 0.95 , x 17.1,故需要志愿者18 名.故选:B
900
【点晴】本题主要考查函数模型的简单应用,属于基础题.
7.(2020•全国 2 卷)4 名同学到 3 个小区参加垃圾分类宣传活动,每名同学只去 1 个小区,每个小区至少
安排 1 名同学,则不同的安排方法共有 种.
【答案】36
【解析】根据题意,有且只有 2 名同学在同一个小区,利用先选后排的思想,结合排列组合和乘法计数原理得解.
【详解】 4 名同学到 3 个小区参加垃圾分类宣传活动,每名同学只去 1 个小区,每个小区至少安排 1 名同
4
学先取 2 名同学看作一组,选法有: C2 6
3
现在可看成是 3 组同学分配到 3 个小区,分法有: A3 6
根据分步乘法原理,可得不同的安排方法6 6 36 种故答案为: 36 .
【点睛】本题主要考查了计数原理的综合应用,解题关键是掌握分步乘法原理和捆绑法的使用,考查了分 析能力和计算能力,属于中档题.
8.(2020•全国 2 卷)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区
某种野生动物的数量,将其分成面积相近的 200 个地块,从这些地块中用简单随机抽样的方法抽取 20 个作为样区,调查得到样本数据(xi,yi)(i=1,2,…,20),其中 xi 和 yi 分别表示第 i 个样区的植物覆盖面积(单位:
20
公顷)和这种野生动物的数量,并计算得xi
i1
20
60 ,yi
i1
20
1200 , (xi
i1
x )2 80 ,
20
(yi
i1
20
y ) 9000 , (x
2
i
i1
x()
yi y ) 800 .
(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);
(2)求样本(xi,yi)(i=1,2,…,20)的相关系数(精确到 0.01);
(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物 数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.
附:相关系数 r=
n
(xi x()
i1
nn
yi y )
,≈1.414.
(x x )2 (y y)2
ii
i1i1
【答案】(1)12000 ;(2) 0.94 ;(3)详见解析
【解析】(1)利用野生动物数量的估计值等于样区野生动物平均数乘以地块数,代入数据即可;
利用公式 r
20
( xi x)( yi y)
i1
20
20
( x x)( y y)
2
i
2
i
i1
i1计算即可;
各地块间植物覆盖面积差异较大,为提高样本数据的代表性,应采用分层抽样.
20
20
1 20 y
1 1200 60
【详解】(1)样区野生动物平均数为 i,
i1
地块数为 200,该地区这种野生动物的估计值为200 60 12000
(2)样本( xi , yi ) (i=1,2,…,20)的相关系数为
20
2 2
(xi x )( yi y )800
20
20
i
i1
( yi y )
i1
80 9000
r i1
0.94 3
(3)由(2)知各样区的这种野生动物的数量与植物覆盖面积有很强的正相关性, 由于各地块间植物覆盖面积差异很大,从俄各地块间这种野生动物的数量差异很大,
采用分层抽样的方法较好地保持了样本结构与总体结构得以执行,提高了样本的代表性, 从而可以获得该地区这种野生动物数量更准确的估计.
4
【点晴】本题主要考查平均数的估计值、相关系数的计算以及抽样方法的选取,考查学生数学运算能力, 是一道容易题.
9.(2020•全国 3 卷)在一组样本数据中,1,2,3,4 出现的频率分别为 p1 , p2 , p3 , p4 ,且 pi 1 ,则下
i 1
面四种情形中,对应样本的标准差最大的一组是()
A. p1 p4 0.1, p2 p3 0.4B. p1 p4 0.4, p2 p3 0.1
C. p1 p4 0.2, p2 p3 0.3D. p1 p4 0.3, p2 p3 0.2
【答案】B
【解析】计算出四个选项中对应数据的平均数和方差,由此可得出标准差最大的一组.
【详解】对于 A 选项,该组数据的平均数为 xA 1 4 0.1 2 3 0.4 2.5 ,
A
方差为 s2 1 2.52 0.1 2 2.52 0.4 3 2.52 0.4 4 2.52 0.1 0.65;对于 B 选项,该组数据的平均数为 xB 1 4 0.4 2 3 0.1 2.5 ,
B
方差为 s2 1 2.52 0.4 2 2.52 0.1 3 2.52 0.1 4 2.52 0.4 1.85 ;对于 C 选项,该组数据的平均数为 xC 1 4 0.2 2 3 0.3 2.5 ,
C
方差为 s2 1 2.52 0.2 2 2.52 0.3 3 2.52 0.3 4 2.52 0.2 1.05 ;
对于 D 选项,该组数据的平均数为 xD 1 4 0.3 2 3 0.2 2.5 ,
D
方差为 s2
1 2.52 0.3 2 2.52 0.2 3 2.52 0.2 4 2.52 0.3 1.45 .
因此,B 选项这一组的标准差最大.故选:B.
【点睛】本题考查标准差的大小比较,考查方差公式的应用,考查计算能力,属于基础题.
10.(2020•全国 3 卷) (x2 2 )6 的展开式中常数项是
x
(用数字作答).
【答案】 240
【解析】写出 x2
2 6
x
二项式展开通项,即可求得常数项.
【详解】 x2
2 6
x
r
其二项式展开通项: T Cr x2 6r 2
Cr x122r (2)r x r Cr (2)r x123r
x
r 16
当12 3r 0 ,解得 r 4
66
2 6
2
442
x x 的展开式中常数项是: C6 2 C6 16 1516 240 .故答案为: 240 .
【点睛】本题考查二项式定理,利用通项公式求二项展开式中的指定项,解题关键是掌握 a b n 的展开
r nr r
n
通项公式Tr 1 C ab ,考查了分析能力和计算能力,属于基础题.
锻炼人次
空气质量等级
[0,200]
(200,400]
(400,600]
1(优)
2
16
25
2(良)
5
10
12
3(轻度污染)
6
7
8
4(中度污染)
7
2
0
11.(2020•全国 3 卷)某学生兴趣小组随机调查了某市 100 天中每天的空气质量等级和当天到某公园锻炼的人次,整理数据得到下表(单位:天):
分别估计该市一天的空气质量等级为 1,2,3,4 的概率;
求一天中到该公园锻炼的平均人次的估计值(同一组中的数据用该组区间的中点值为代表);
人次≤400
人次>400
空气质量好
空气质量不好
若某天的空气质量等级为 1 或 2,则称这天“空气质量好”;若某天的空气质量等级为 3 或 4,则称这天“空气质量不好”.根据所给数据,完成下面的 2×2 列联表,并根据列联表,判断是否有 95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
附: K2
n(ad bc)2
,
(a b)(c d)(a c)(b d)
【答案】(1)该市一天的空气质量等级分别为1、2 、3 、4 的概率分别为0.43 、0.27 、0.21 、0.09 ;(2)
350 ;(3)有,理由见解析.
【解析】(1)根据频数分布表可计算出该市一天的空气质量等级分别为1、2 、3 、4 的概率;
利用每组的中点值乘以频数,相加后除以100 可得结果;
根据表格中的数据完善 2 2 列联表,计算出 K2 的观测值,再结合临界值表可得结论.
【详解】(1)由频数分布表可知,该市一天的空气质量等级为1的概率为 2 16 25 0.43 ,等级为 2 的
100
概率为 5 10 12 0.27 ,等级为3 的概率为 6 7 8 0.21 ,等级为 4 的概率为 7 2 0 0.09 ;
P(K2≥k)
0.050
0.010
0.001
k
3.841
6.635
10.828
100
100
100
(2)由频数分布表可知,一天中到该公园锻炼的人次的平均数为100 20 300 35 500 45 350
100
(3) 2 2 列联表如下:
人次 400
人次 400
100 338 37 22 2
K 2 5.820 3.841 ,
55 45 70 30
因此,有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关.
【点睛】本题考查利用频数分布表计算频率和平均数,同时也考查了独立性检验的应用,考查数据处理能 力,属于基础题.
12.(2020•江苏卷)已知一组数据 4, 2a, 3 a, 5, 6 的平均数为 4,则 a 的值是 .
【答案】2
【解析】根据平均数的公式进行求解即可.
【详解】∵数据 4, 2a, 3 a, 5, 6 的平均数为 4∴ 4 2a 3 a 5 6 20 ,即 a 2 .故答案为:2.
【点睛】本题主要考查平均数的计算和应用,比较基础.
13.(2020•江苏卷)将一颗质地均匀的正方体骰子先后抛掷 2 次,观察向上的点数,则点数和为 5 的概率是
.
1
【答案】
9
【解析】分别求出基本事件总数,点数和为 5 的种数,再根据概率公式解答即可.
【详解】根据题意可得基本事件数总为6 6 36 个.
点数和为 5 的基本事件有1, 4 , 4,1 , 2, 3 , 3, 2共 4 个.
空气质量不好
33
37
空气质量好
22
8
∴出现向上的点数和为 5 的概率为 P
4 1 .故答案为: 1 .
3699
【点睛】本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.
14.(2020•新全国 1 山东)6 名同学到甲、乙、丙三个场馆做志愿者,每名同学只去 1 个场馆,甲场馆安排
1 名,乙场馆安排 2 名,丙场馆安排 3 名,则不同的安排方法共有()
A. 120 种B. 90 种
C. 60 种D. 30 种
【答案】C
【解析】分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.
6
【详解】首先从6 名同学中选1名去甲场馆,方法数有C1 ;
5
65
然后从其余5 名同学中选2 名去乙场馆,方法数有C2 ;最后剩下的3 名同学去丙场馆. 故不同的安排方法共有C1 C 2 6 10 60 种.故选:C
【点睛】本小题主要考查分步计数原理和组合数的计算,属于基础题.
15.(2020•新全国 1 山东)某中学的学生积极参加体育锻炼,其中有 96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是
()
A. 62%B. 56%
C. 46%D. 42%
【答案】C
【解析】记“该中学学生喜欢足球”为事件 A ,“该中学学生喜欢游泳”为事件 B ,则“该中学学生喜欢足球或游泳”为事件 A B ,“该中学学生既喜欢足球又喜欢游泳”为事件 A B ,然后根据积事件的概率公式 P( A B) P( A) P(B) P( A B) 可得结果.
【详解】记“该中学学生喜欢足球”为事件 A ,“该中学学生喜欢游泳”为事件 B ,则“该中学学生喜欢足球或游泳”为事件 A B ,“该中学学生既喜欢足球又喜欢游泳”为事件 A B ,
则 P( A) 0.6 , P(B) 0.82 , P A B 0.96 ,
所以 P( A B) P( A) P(B) P( A B) 0.6 0.82 0.96 0.46
所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为 46% .故选:C.
【点睛】本题考查了积事件的概率公式,属于基础题.
16.(2020•新全国 1 山东)信息熵是信息论中的一个重要概念.设随机变量 X 所有可能的取值为1, 2,, n ,
nn
且 P( X i) pi 0(i 1, 2,, n), pi 1 ,定义 X 的信息熵 H ( X ) pi lg2 pi .()
若 n=1,则 H(X)=0
i 1
i 1
若 n=2,则 H(X)随着 p1 的增大而增大
若 pi
1 (i 1, 2,, n) ,则 H(X)随着 n 的增大而增大
n
若 n=2m,随机变量 Y 所有可能的取值为1, 2,, m ,且 P(Y j) p j p2m 1 j ( j 1, 2, , m) ,则 H(X)≤H(Y)
【答案】AC
【解析】对于 A 选项,求得 H X ,由此判断出 A 选项的正确性;对于 B 选项,利用特殊值法进行排除; 对于 C 选项,计算出 H X ,利用对数函数的性质可判断出 C 选项的正确性;对于 D 选项,计算出H X , H Y ,利用基本不等式和对数函数的性质判断出 D 选项的正确性.
【详解】对于 A 选项,若 n 1 ,则i 1, p1 1,所以 H X 1lg2 1 0 ,所以 A 选项正确.对于 B 选项,若 n 2 ,则i 1, 2 , p2 1 p1 ,
所以 H X p1 lg2 p1 1 p1 lg2 1 p1 ,
当 p 1 时, H X 1 lg 1 3 lg 3 ,
14 4
2 44
2 4
当p 3 时, H X 3 lg
3 1 lg
1
,两者相等,所以 B 选项错误.
14 4
2 44
2 4
对于 C 选项,若 pi
1 i 1, 2,, n ,则
n
H X 1 lg
n
1 n lg
2
n
1 lg n ,
2 n2
则 H X 随着 n 的增大而增大,所以 C 选项正确.
对于 D 选项,若 n 2m ,随机变量Y 的所有可能的取值为1, 2,, m ,且 P Y j pj p2m1 j
2m
( j 1, 2,, m ). H X p lg
2m
1
p
p p lg
2
i
i1
2ii
i1i
p1 lg2
1 p
p
2 lg2 p
p
2 m1 lg2 p
p2 m
lg2 p.
1
1
1
122 m12 m
H Y p p
lg
1 p p
lg
1 p p
lg1
12m
2 p p
22m12 p p
mm12 p p
12m
22m1
mm1
p1 lg2
1
p p
p2 lg2 p p
p
2 m1 lg2 p p
p2 m
lg2
1
1
p p由于
1
12 m
22 m 122 m 112 m
p 0i 1, 2,, 2m,所以 1
1,所以lg
1 lg1,
ipp p
2 p2
p p
ii2m1iii2m1i
1
所以 pi lg2 p
pi lg2
1
p p
,所以 H X H Y ,所以 D 选项错误.故选:AC
ii2m1i
【点睛】本小题主要考查对新定义“信息熵”的理解和运用,考查分析、思考和解决问题的能力,涉及对数运 算和对数函数及不等式的基本性质的运用,属于难题.
2
SO2
PM 2.5
[0, 50]
(50,150]
(150, 475]
[0, 35]
32
18
4
(35, 75]
6
8
12
(75,115]
3
7
10
17.(2020•新全国 1 山东)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100 天空气中的PM 2.5 和SO 浓度(单位: μg/m3 ),得下表:
估计事件“该市一天空气中PM 2.5 浓度不超过75 ,且SO2 浓度不超过150 ”的概率;
根据所给数据,完成下面的 2 2 列联表:
根据(2)中的列联表,判断是否有99% 的把握认为该市一天空气中PM 2.5 浓度与SO2 浓度有关?
SO2
PM 2.5
[0,150]
(150, 475]
[0, 75]
(75,115]
附: K2
n(ad bc)2
,
(a b)(c d)(a c)(b d)
P(K 2 k )
0.0500.0100.001
k3 8416.63510.828
【答案】(1) 0.64 ;(2)答案见解析;(3)有.
【解析】(1)根据表格中数据以及古典概型的概率公式可求得结果;
根据表格中数据可得 2 2 列联表;
计算出 K2 ,结合临界值表可得结论.
【详解】(1)由表格可知,该市 100 天中,空气中的 PM 2.5 浓度不超过 75,且SO2 浓度不超过 150 的天数有32 6 18 8 64 天,
所以该市一天中,空气中的 PM 2.5 浓度不超过 75,且SO 浓度不超过 150 的概率为 64
0.64 ;
2
(2)由所给数据,可得 2 2 列联表为:
100
(3)根据 2 2 列联表中的数据可得
SO2
PM 2.5
0,150
150, 475
合计
0, 75
64
16
80
75,115
10
10
20
合计
74
26
100
K 2
n(ad bc)2
100(6410 1610)2
3600 7.4844 6.635 ,
(a b)(c d )(a c)(b d )80 20 74 26
481
因为根据临界值表可知,有99% 的把握认为该市一天空气中 PM 2.5 浓度与SO2 浓度有关.
【点睛】本题考查了古典概型的概率公式,考查了完善 2 2 列联表,考查了独立性检验,属于中档题. 18.(2020•天津卷)从一批零件中抽取 80 个,测量其直径(单位: mm ),将所得数据分为 9 组:
[5.31, 5.33),[5.33, 5.35),,[5.45, 5.47],[5.47, 5.49],并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间[5.43, 5.47) 内的个数为()
A. 10B. 18C. 20D. 36
【答案】B
【解析】根据直方图确定直径落在区间5.43, 5.47 之间的零件频率,然后结合样本总数计算其个数即可.
【详解】根据直方图,直径落在区间5.43, 5.47 之间的零件频率为: 6.25 5.00 0.02 0.225 , 则区间5.43, 5.47 内零件的个数为: 80 0.225 18 .故选:B.
【点睛】本题主要考查频率分布直方图的计算与实际应用,属于中等题.
19.(2020•天津卷)在 x
2 5
x2
的展开式中, x2 的系数是 .
【答案】10
【解析】写出二项展开式的通项公式,整理后令 x 的指数为 2,即可求出.
2 5 2 r
【详解】因为 x
的展开式的通项公式为T
Cr x5r
Cr 2r x53r r 0,1, 2, 3, 4, 5 ,令
x2
r 15
x2 5
5
5 3r 2 ,解得 r 1 .所以 x2 的系数为C1 2 10 .故答案为:10 .
【点睛】本题主要考查二项展开式的通项公式的应用,属于基础题.
11
20.(2020•天津卷)已知甲、乙两球落入盒子的概率分别为 2 和 3 .假定两球是否落入盒子互不影响,则
甲、乙两球都落入盒子的概率为 ;甲、乙两球至少有一个落入盒子的概率为 .
1
【答案】(1).
6
2
(2).
3
【解析】根据相互独立事件同时发生的概率关系,即可求出两球都落入盒子的概率;同理可求两球都不落
入盒子的概率,进而求出至少一球落入盒子的概率.
【详解】甲、乙两球落入盒子的概率分别为 1 , 1 ,且两球是否落入盒子互不影响,
2 3
所以甲、乙都落入盒子的概率为
1 1 1 ,
236
甲、乙两球都不落入盒子的概率为(1 1) (1 1) 1 ,
233
212
所以甲、乙两球至少有一个落入盒子的概率为
3
.故答案为:;.
63
【点睛】本题主要考查独立事件同时发生的概率,以及利用对立事件求概率,属于基础题.
21.(2020•浙江卷)设1 2x5
a a x a x2 a x3 a x4 a x5 , 则 a5= ;a1+a2 + a3= .
123456
【答案】(1). 80
(2). 122
【解析】利用二项式展开式的通项公式计算即可.
【详解】 (1 2x)5 的通项为 T Cr (2x)r 2r Cr xr ,令 r 4 ,则 T 24 C 4 x4 80x4 ,故 a 80 ;
r155555
a a a 21C1 23 C3 25 C5 122 .故答案为:80;122
135555
【点晴】本题主要考查利用二项式定理求指定项的系数问题,考查学生的数学运算能力,是一道基础题. 22.(2020•浙江卷)一个盒子里有 1 个红 1 个绿 2 个黄四个相同的球,每次拿一个,不放回,拿出红球即停, 设拿出黄球的个数为,则 P( 0) ; E() .
1
【答案】(1).(2). 1
3
【解析】先确定 0 对应事件,再求对应概率得结果;第二空,先确定随机变量,再求对应概率,最后根据数学期望公式求结果.
【详解】因为 0 对应事件为第一次拿红球或第一次拿绿球,第二次拿红球,
所以 P( 0) 1 1 1 1 ,随机变量 0,1, 2 , P( 1) 2 1 2 1 1 1 2 1 1 ,
4433434324323
P( 2) 1 1 1 1 ,所以 E() 0 1 1 1 2 1 1 .故答案为: 1 ;1.
3333333
【点睛】本题考查古典概型概率、互斥事件概率加法公式、数学期望,考查基本分析求解能力,属基础题.
23.(2020•上海卷)从 6 人中挑选 4 人去值班,每人值班 1 天,第一天需要 1 人,第二天需要 1 人,第三天
需要 2 人,则有种排法。
【答案】180
2024年高考数学大题--概率统计题型分类汇编: 这是一份2024年高考数学大题--概率统计题型分类汇编,文件包含概率统计解析版pdf、概率统计学生版pdf等2份试卷配套教学资源,其中试卷共82页, 欢迎下载使用。
2012-2021山东春季高考数学试题分类汇编 专题九 概率与统计: 这是一份2012-2021山东春季高考数学试题分类汇编 专题九 概率与统计,文件包含9-专题九概率与统计答案版docx、9-专题九概率与统计原卷版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
2022年高考数学真题类汇编:05排列组合与概率统计知识点分类: 这是一份2022年高考数学真题类汇编:05排列组合与概率统计知识点分类,文件包含2022年高考数学真题类汇编05排列组合与概率统计知识点分类解析版docx、2022年高考数学真题类汇编05排列组合与概率统计知识点分类原卷版docx等2份试卷配套教学资源,其中试卷共15页, 欢迎下载使用。