人教版新课标A选修2-2第一章 导数及其应用1.2导数的计算教案配套课件ppt

这是一份人教版新课标A选修2-2第一章 导数及其应用1.2导数的计算教案配套课件ppt，共31页。PPT课件主要包含了自主学习新知突破，几个常用函数的导数，合作探究课堂互动，求函数的导数，求某一点处的导数，导数几何意义的应用等内容，欢迎下载使用。

1．掌握几个常用函数的导数，并能进行简单的应用．2．掌握基本初等函数的导数公式，并能进行简单的应用．
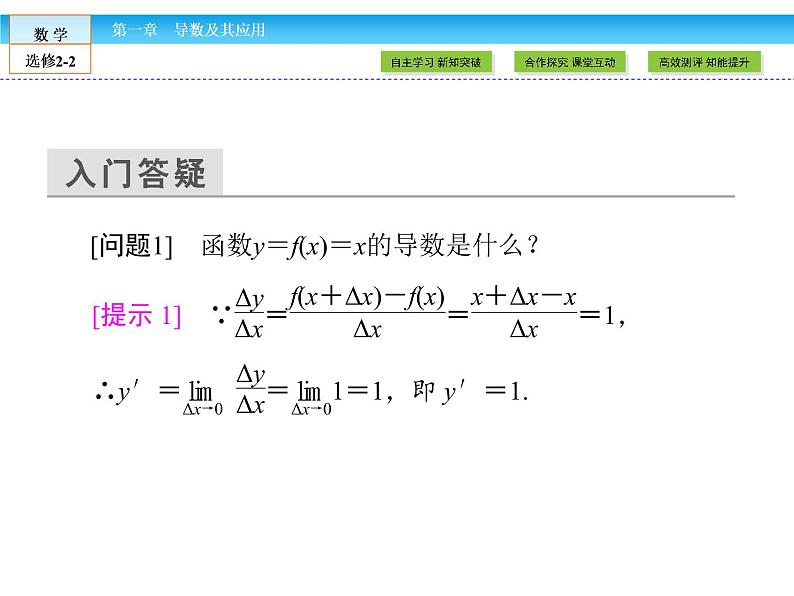
[问题1]　函数y＝f(x)＝x的导数是什么？
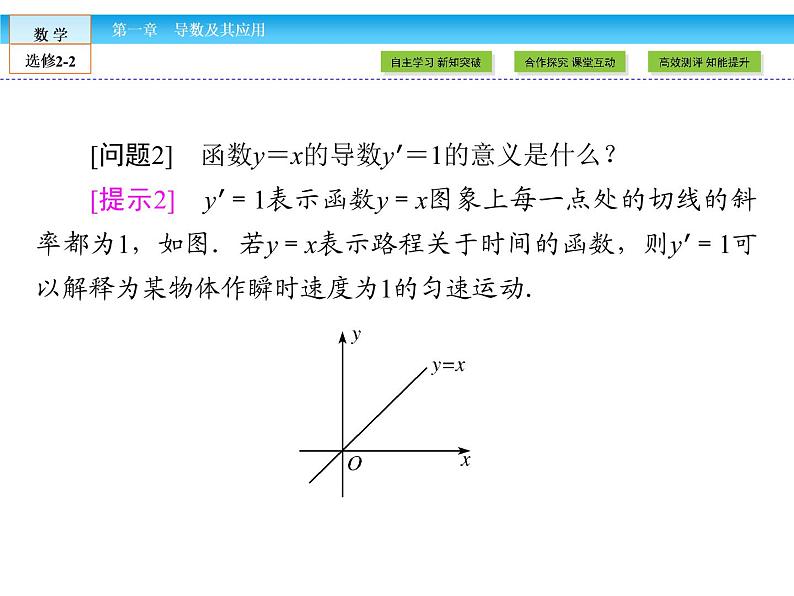
[问题2]　函数y＝x的导数y′＝1的意义是什么？[提示2]　y′＝1表示函数y＝x图象上每一点处的切线的斜率都为1，如图．若y＝x表示路程关于时间的函数，则y′＝1可以解释为某物体作瞬时速度为1的匀速运动．
基本初等函数的导数公式
0αxα－1cs x－sin xaxln a(a>0)ex
2．对基本初等函数的导数公式的理解不要求根据导数定义推导这八个基本初等函数的导数公式，只要求能够利用它们求简单函数的导数，在学习中，适量的练习对于熟悉公式是必要的，但应避免形式化的运算练习．
解析：　因常数的导数等于0，故选C.答案：　C
2．曲线y＝x3上切线平行或重合于x轴的切点坐标(　　)A．(0,0) B．(0,1)C．(1,0) D．以上都不是解析：　(x3)′＝3x2，若切线平行或重合于x轴则切线斜率k＝0，即3x2＝0得x＝0，∴y＝0，即切点为(0,0)．故选A.答案：　A
3．函数f(x)＝sin x，则f′(6π)＝________.解析：　f′(x)＝cs x，所以f′(6π)＝1.答案：　1
4．求下列函数的导数：(1)y＝x8；(2)y＝π＋1；(3)y＝lg2x；(4)y＝2e3；(5)y＝2cs x.
求下列函数的导数：[思路点拨]　解答本题可先将解析式化为基本初等函数，再利用公式求导．
(1)y′＝－3x－4.(2)y′＝3xln 3.
求简单函数的导函数有两种基本方法：(1)用导数的定义求导，但运算比较繁杂；(2)用导数公式求导，可以简化运算过程、降低运算难度．解题时根据所给问题的特征，将题中函数的结构进行调整，再选择合适的求导公式．
[思路点拨]　先求导函数，再由导数值求P点横坐标．
1.在某点处的导数与导函数是不同的，在某点处的导数是指在该点处的导数值．2．求函数在某点处的导数需要先对原函数进行化简，然后求导，最后将变量的值代入导函数便可求解．
已知曲线方程y＝x2，求过点B(3,5)且与曲线相切的直线方程．[思路点拨]　解决切线问题的关键是求切点的坐标，要注意区分是曲线在某点处的切线还是过某点的切线．
1.求过点P的切线方程时应注意，P点在曲线上还是在曲线外，两种情况的解法是不同的．2．解决此类问题应充分利用切点满足的三个关系：一是切点坐标满足曲线方程；二是切点坐标满足对应切线的方程；三是切线的斜率是曲线在此切点处的导数值．
3．已知点P(－1,1)，点Q(2,4)是曲线y＝x2上的两点，求与直线PQ垂直的曲线y＝x2的切线方程．
◎求下列函数的导数．(1)y＝(－x)8；(2)y＝(ax)5(a为不等于0的常数)．【错解】　(1)y′＝8(－x)7＝－8x7.(2)y′＝5(ax)4＝5a4x4.【错因】　两小题的解法都是错用了公式(xn)′＝nxn－1，本公式成立的条件是底数是自变量x本身，而不是关于自变量x的代数式，因此本题直接套用幂函数的求导公式是错误的．