人教版九年级上册第二十四章 圆24.3 正多边形和圆课时训练

这是一份人教版九年级上册第二十四章 圆24.3 正多边形和圆课时训练，共10页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
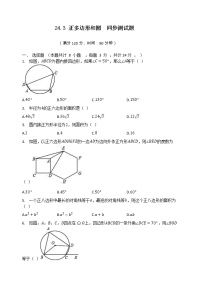
1. 如图，由等边三角形、正方形、圆组成的轴对称图案中，等边三角形与三个正方形的面积和的比值为（ ）
A. 32 B. 1 C. 3 D. 332
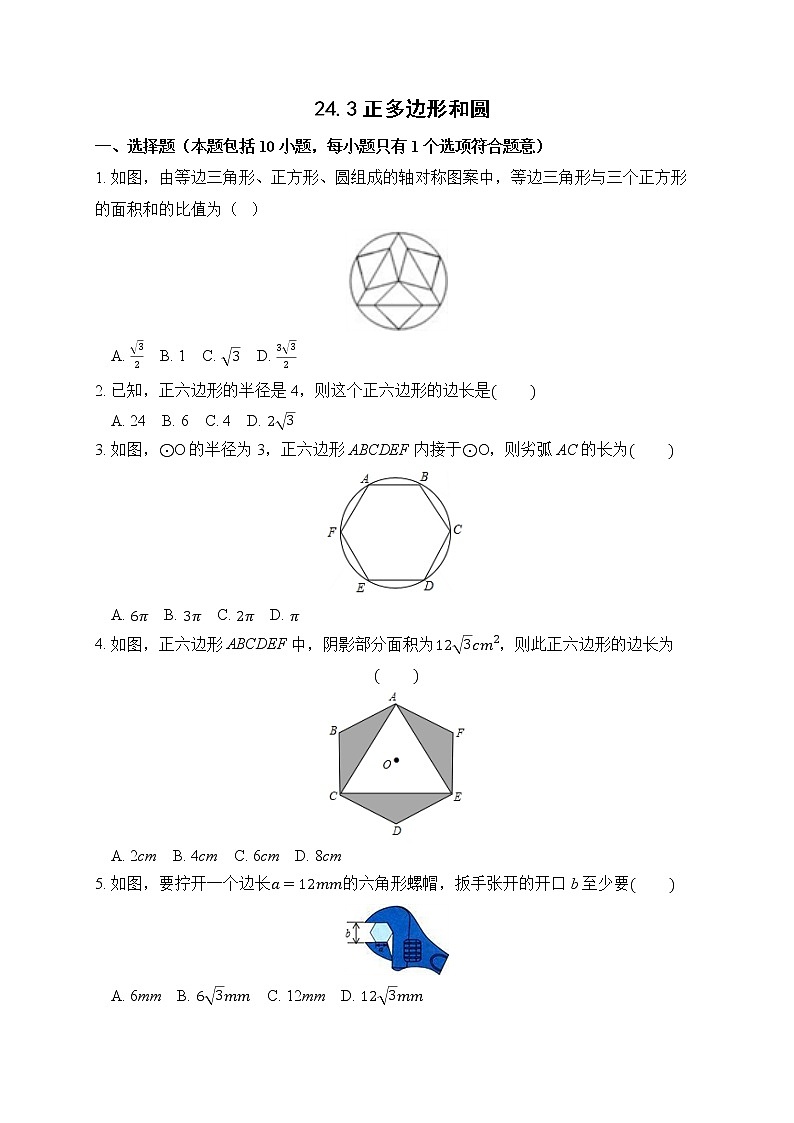
2. 已知，正六边形的半径是4，则这个正六边形的边长是( )
A. 24 B. 6 C. 4 D. 23
3. 如图，⊙O的半径为3，正六边形ABCDEF内接于⊙O，则劣弧AC的长为( )
A. 6π B. 3π C. 2π D. π
4. 如图，正六边形ABCDEF中，阴影部分面积为123cm2，则此正六边形的边长为( )
A. 2cm B. 4cm C. 6cm D. 8cm
5. 如图，要拧开一个边长a=12mm的六角形螺帽，扳手张开的开口b至少要( )
A. 6mm B. 63mm C. 12mm D. 123mm
6. 下列关于圆的叙述正确的有( )
①圆内接四边形的对角互补；②相等的圆周角所对的弧相等；③正多边形内切圆的半径与正多边形的半径相等；④同圆中的平行弦所夹的弧相等．
A. 1个 B. 2个 C. 3个 D. 4个
7. 如图，以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系，顶点A，D在x轴上，则点C的坐标为( )

A. 1，-2 B. 1，-2 C. 1，-3 D. -1，-3
8. 如图，半径为1的⊙O与正六边形ABCDEF相切于点A、D，则弧AD的长为( )

A. 16π B. 13π C. 23π D. 56π
9. 如图，正方形ABCD内接于半径为2的⊙O，则图中阴影部分的面积为( )
A. π+1 B. π+2 C. π-1 D. π-2
10. 下列说法正确的是( )
A. 圆内接正六边形的边长与该圆的半径相等
B. 在平面直角坐标系中，不同的坐标可以表示同一点
C. 一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D. 将△ABC绕A点按顺时针方向旋转60∘得△ADE，则△ABC与△ADE不全等
二、解答题（本题包括4小题）
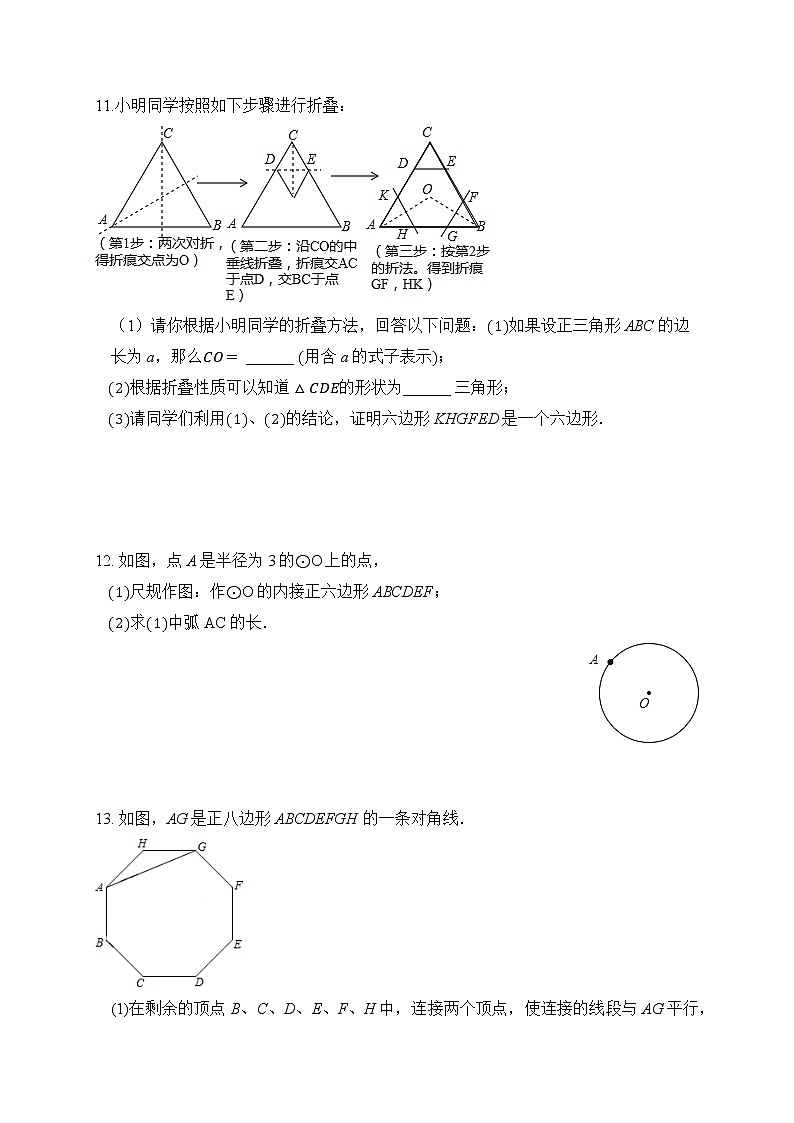
11.小明同学按照如下步骤进行折叠：

（1）请你根据小明同学的折叠方法，回答以下问题：(1)如果设正三角形ABC的边长为a，那么CO= ______ (用含a的式子表示)；
(2)根据折叠性质可以知道△CDE的形状为______ 三角形；
(3)请同学们利用(1)、(2)的结论，证明六边形KHGFED是一个六边形．
12. 如图，点A是半径为3的⊙O上的点，
(1)尺规作图：作⊙O的内接正六边形ABCDEF；
(2)求(1)中弧AC的长．
13. 如图，AG是正八边形ABCDEFGH的一条对角线．
(1)在剩余的顶点B、C、D、E、F、H中，连接两个顶点，使连接的线段与AG平行，并说明理由；
(2)两边延长AB、CD、EF、GH，使延长线分别交于点P、Q、M、N，若AB=2，求四边形PQMN的面积．
14. (1)如图，EF是⊙O的直径，请仅用尺规作出该圆的内接正方形ABCD，要求所作正方形的一组对边AD、BC垂直于EF见示意图；不写作法，但须保留作图痕迹)；
(2)连接EA、EB，求出∠EAD、∠EBC的度数．

参考答案
一、选择题
1. 【答案】A
【解析】依题意知，过直角三角形顶点过圆心做直线垂直于底边。图中等边三角形的高h=32r（设r为圆的半径），设底边边长为2x，根据勾股定理可得，（2x）2-x2=（32r）2，解得2x=3r。∴等边三角形面积S1=
·32r·3=。又∵正方形的对角线等于圆的半径，所以3个正方形的面积S2=3×2×r·r=32r2。∴=
考点：等边三角形，圆和正方形这类对称图形的特殊性
点评：难度较低。考查学生对几何图形的认识与灵活运算能力。运用勾股定理，等边三角形每个角
60°得出辅助线作用下的小直角为30°特殊直角三角形，30°角对应的直角边等于斜边的一半。正方形对角线把正方形平分成两个全等直角三角形等。
2.【答案】C
【解析】如图所示，连接OB、OC；∵此六边形是正六边形，∴∠BOC=360°60=60°，∵OB=OC=4，∴△BOC是等边三角形，∴OB=OC=BC=4．故选C．
3. 【答案】C
【解析】如图所示,∵ABCDEF为正六边形，∴∠AOB=360°×16=60°，∴∠AOC=120°，∴AC的长为120×π×3180=2π．故选C．
4. 【答案】B
【解析】由正六边形可分成六个全等的等边三角形，则阴影部分的面积与中间的正三角形的面积相等，即阴影部分的面积为正六边形的面积的一半.设边长为R，所以有，所以R=4cm.故选B.
5. 【答案】D
【解析】设正多边形的中心是O，其一边是AB，∴∠AOB=∠BOC=60°，∴OA=OB=AB=OC=BC，∴四边形ABCO是菱形，∵AB=12mm，∠AOB=60°，∴cs∠BAC=AMAB，∴AM=12×32=63，∵OA=OC，且∠AOB=∠BOC，∴AM=MC=12AC，∴AC=2AM=123mm．故选D．
6. 【答案】B
【解析】①圆内接四边形的对角互补；正确；②相等的圆周角所对的弧相等；错误；③正多边形内切圆的半径与正多边形的半径相等；错误；④同圆中的平行弦所夹的弧相等；正确；正确的有2个，故选B．
7.【答案】C
【解析】连接OC．∵∠COD=60°，OC=OD，∴△COD是等边三角形，∴OC=OD=2.设BC交y轴于G，则∠GOC=30°.在Rt△GOC中，∵∠GOC=30°，OC=2，∴GC=1，OG=，∴C(1，-).故选C.
8. 【答案】C
【解析】连接OA，OD，∵⊙O与正六边形ABCDEF相切于点A、D，∴∠OAF=∠ODE=90°，∵∠E=∠F=120°，∴∠AOD=540°-90°-90°-120°-120°=120°，∴AD的长为120π×1180=2π3,故选C．
9. 【答案】D
【解析】连接AO，DO，∵ABCD是正方形， ∴∠AOD=90°，AD=OA2+OD2=22，圆内接正方形的边长为22，所以阴影部分的面积=14 [4π-（22）2]=π-2．故选D．
10.【答案】A
【解析】如图，∠AOB=360°6=60°，OA=OB，∴△AOB是等边三角形，∴AB=OA，∴圆内接正六边形的边长与该圆的半径相等，A正确；在平面直角坐标系中，不同的坐标可以表示不同一点，B错误；一元二次方程ax2+bx+c=0（a≠0）不一定有实数根，C错误；根据旋转变换的性质可知，将△ABC绕A点按顺时针方向旋转60°得△ADE，则△ABC与△ADE全等，D错误；故选A．
二、解答题
11. 【答案】 (1) 33a (2) 等边
【解析】（1）根据折叠的性质即可得到结论；（2）根据折叠的性质即可得到结论；（3）由（2）知△CDE为等边三角形，根据等边三角形的性质得到CD=CE=DE=12CO÷cs30°=13a，求得∠ADE=∠BED=120°，同理可得，AH=AK=KH=13a，BG=BF=GF=13a，∠CKH=∠BHK=120°，由于AB=BC=AC=a，于是得到结论．
解：（1）∵正三角形ABC的边长为a，
由折叠的性质可知，点O是三角形的重心，
∴CO=33a；
故答案为：33a；
（2）△CDE为等边三角形；
故答案为：等边；
（3）由（2）知△CDE为等边三角形，
∴CD=CE=DE=12CO÷cs30°=13a，
∠ADE=∠BED=120°，
同理可得，AH=AK=KH=13a，BG=BF=GF=13a，∠CKH=∠BHK=120°，
∵AB=BC=AC=a，
∴DE=DK=KH=HG=GF=FE=13a，∠ADE=∠BED=∠CKH=∠BHK=∠CFG=∠AGF=120°，
∴六边形KHGFED是一个正六边形．
12. 【答案】（1）见解析；（2）2π
【解析】（1）由正六边形ABCDEF的中心角为60°，可得△OAB是等边三角形，继而可得正六边形的边长等于半径，则可画出⊙O的内接正六边形ABCDEF；（2）由（1）可求得∠AOC=120°，继而求得（1）中AC的长．
解：（1）首先连接OA，然后以A为圆心，OA长为半径画弧，交⊙O于B，F，再分别以B，F为圆心，OA长为半径画弧，交⊙O于点E，C，在以C为圆心，OA长为半径画弧，交⊙O于点D，则正六边形ABCDEF即为所求；
（2）∵正六边形ABCDEF是⊙O的内接正六边形
∴∠AOC=360°6×2=120°，
∵⊙O的半径为3，
∴AC的长为：120×π×3180=2π．
13. 【解析】（1）利用已知得出正八边形,它的内角都为135°,再利用正八边形ABCDEFGH关于直线BF对称,得出∠2+∠3=180°,进而得出答案,（2）根据题意得出△PAH≌△QCB≌△MDE,则PA=QB=QC=MD,即PQ=QM,故四边形PQMN是正方形,进而求出PQ的长即可得出答案.
解：（1）连接BF,则有BF∥AG,理由如下:
∵ABCDEFGH是正八边形,∴它的内角都为135°,
又∵HA=HG,∴∠1=22.5°,
从而∠2=135°﹣∠1=112.5°,
由于正八边形ABCDEFGH关于直线BF对称,
∴∠3＝12135°=67.5°
即∠2+∠3=180°,故BF∥AG,
（2）根据题设可知∠PHA=∠PAH=45°,
∴∠P=90°,同理可得∠Q=∠M=90°,
∴四边形PQMN是矩形．
又∵∠PHA=∠PAH=∠QBC=∠QCB=∠MDE=∠MED=45°,AH=BC=DE,
∴△PAH≌△QCB≌△MDE,
∴PA=QB=QC=MD,即PQ=QM,
故四边形PQMN是正方形．
在Rt△PAB中,
∵∠PAH=45°,AB=2,
∴ PA=ABsin45°=2×22=2,
∴ PQ=PA+AB+BQ=2+2+2=22+2,
故四边形PQMN的面积 =22+22=12+82.
14.【答案】（1）见解析；（2）67.5°
【解析】（1）作出八等分点，即可得到圆内接正方形；（2）求出相应圆心角的度数，根据圆周角等于圆心角的一半，即可解答．
解：（1）作①EF的中垂线，
②直角的平分线OD，
③8等分弧，完成正方形．
（2）连接OD，OC，
因为ED=18圆周，所以∠EOD=360°×18=45°，
所以∠EAD=45°×12=22.5°．
因为EDC=3ED，
所以∠EBC=3∠EAD=3×22.5°=67.5°．