小升初数学第六讲《立体图形计算》人教版无答案

这是一份小升初数学第六讲《立体图形计算》人教版无答案，共5页。

2、正方体的体积=棱长×棱长×棱长 V= a3
3、圆锥的体积=底面积×高÷3
V=Sh÷3=πr2 h÷3=π(d÷2) 2 h÷3=π(C÷2÷π) 2h÷3
4、长方体（正方体、圆柱体）的体积=底面积×高 V=Sh
5、圆柱的体积=底面积×高 V=Sh
V=πr 2h=π(d÷2) 2 h=π(C÷2÷π) 2 h
【例题精讲】
例1：如右图，在一个棱长为10的立方体上截取一个长为8，
宽为3，高为2的小长方体，那么新的几何体的表面积是多少？
例2：右图是一个边长为4厘米的正方体，分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体，做成一种玩具．它的表面积是多少平方厘米?（图中只画出了前面、右面、上面挖去的正方体）

例3：有30个边长为1米的正方体，在地面上摆成右上图的形式，然后把露出的表面涂成红色．求被涂成红色的表面积．
例4：一张长方形铁皮，如图剪下阴影部分制成圆柱体（单位：分米），求这个圆柱体的表面积。（提示：圆桶盖的周长等于长方形铁皮的长。）

例5：有一个圆柱体的零件，高厘米，底面直径是厘米，零件的一端有一个圆柱形的圆孔，圆孔的直径是厘米，孔深厘米(见右图)．如果将这个零件接触空气的部分涂上防锈漆，那么一共要涂多少平方厘米？

例6：一个拧紧瓶盖的瓶子里面装着一些水(如图)，由图中的数据可推知瓶子的容积是_______ 立方厘米．(取)
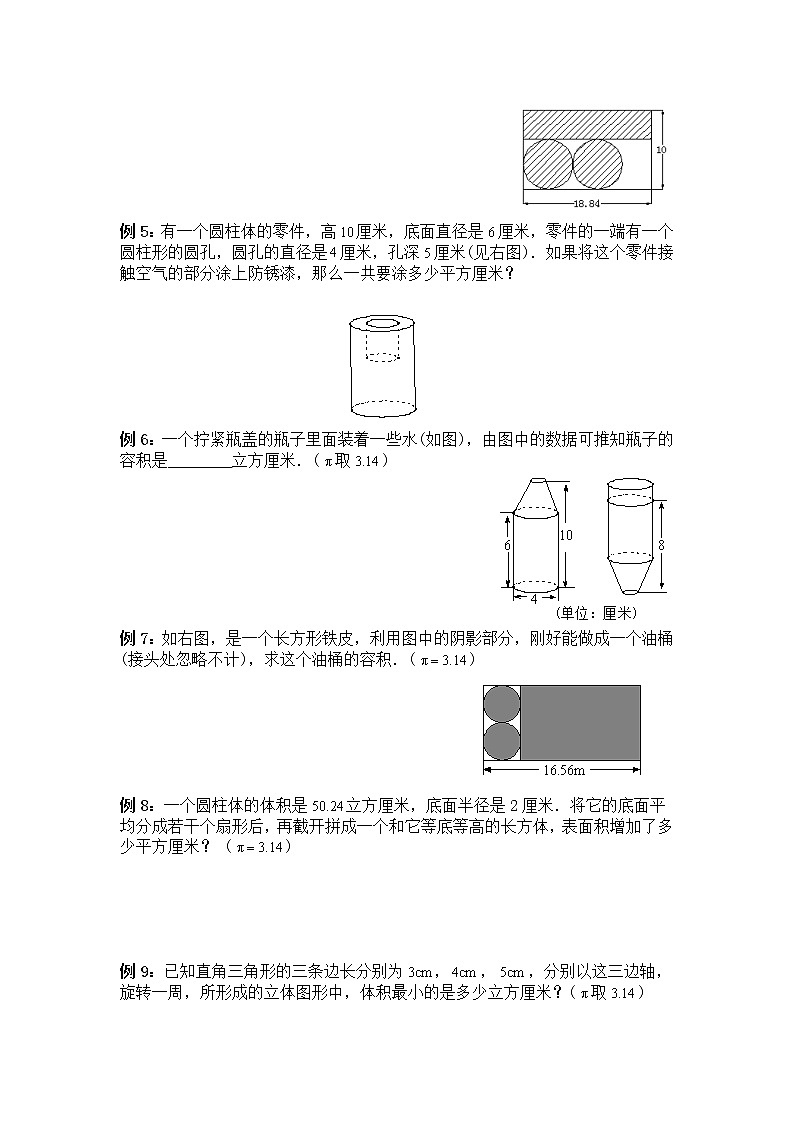
例7：如右图，是一个长方形铁皮，利用图中的阴影部分，刚好能做成一个油桶(接头处忽略不计)，求这个油桶的容积．()
例8：一个圆柱体的体积是立方厘米，底面半径是2厘米．将它的底面平均分成若干个扇形后，再截开拼成一个和它等底等高的长方体，表面积增加了多少平方厘米？ ()
例9：已知直角三角形的三条边长分别为，，，分别以这三边轴，旋转一周，所形成的立体图形中，体积最小的是多少立方厘米？(取)
例10：已知水结成冰，体积增加。右下图是一只瓶子，它的上部分是高位20厘米的圆柱，底面直径是6厘米，下部分是高为5厘米的圆锥。当圆瓶的冰全部融化成水时，求水面的高度（说明：水面高度是指圆锥顶点到水面的距离，结果保留一位小数）
例11：某工人用薄木板钉成一个长方体的邮件包装箱，并用尼龙编织条如图11-9所示在三个方向上加固．所用尼龙编织条的长分别为305厘米、405厘米、405厘米．若每个尼龙条加固时接头处都重叠5厘米，则这个长方体包装箱的体积是多少立方米?
【大显身手】
1、长方体有（ ）个面，（ ）条棱，（ ）个顶点，相对的棱长度（ ），相对的面（ ）。
2、圆柱的侧面展开是一个（ ），它的长是圆柱（ ），它的宽是圆柱的（ ）。
3、一个长方体的长5厘米，宽3厘米，高2厘米，它的最大的一个面是（ ）面，面积是（ ）平方厘米。这个长方体的表面积是（ ）平方厘米，体积是（ ）立方厘米。
4、一个直径8厘米，长2米的圆柱形铁皮通风管，沿着高剪开得到一个长方形，它的长是（ ）米，宽是（ ）米。
5、用边长是6.28厘米的正方形纸围成一个最大的圆柱形纸筒，这个纸筒的高是（ ）厘米，体积是（ ）立方厘米。
6、一个正方体的棱长总和是48厘米，它的表面积是（ ）平方厘米，体积是（ ）立方厘米。
7、一个圆锥的体积是24立方厘米，底面积是8平方厘米，它的高是（ ）厘米。
8、把三个棱长为1分米的正方体拼成一个长方体，这个长方体的表面积是（ ）平方分米，体积是（ ）立方分米。
9、把一个棱长是a米的正方体木材，任意截成两个小长方体后，表面积比原来多（ ）平方米。
10、把一个棱长是3厘米的正方体，削成一个最大的圆柱，它的体积是（ ）立方厘米。
11、一个圆柱体木材，底面直径和高都是6厘米，它的侧面积是（ ）平方厘米，体积是（ ）立方厘米。如果加工成最大的圆锥，这个圆锥的体积是（ ）立方厘米。
12、一个圆柱的高是9.42厘米,侧面展开是一个正方形,它的底面直径是( )厘米。
13、一个圆柱的高截去2厘米，表面积就减少12.56平方厘米，这个圆柱的底面直径是（ ）厘米。
14、一个圆柱的侧面展开是边长31.4厘米的正方形,这个圆柱的底面积是( )平方厘米。
15、如左下图，长方体的长、宽、高分别是（ ）、（ ）、（ ）。计算它的占地面积要用（ ）×（ ）；计算它的前面的面积要用（ ）×（ ）；计算它的左面的面积要用（ ）×（ ）。它的棱长总和是（ ）。
10分米
5分米
6分米
5厘米
16、右上图正方体的棱长和是（ ），占地面积是（ ），体积是（ ），表面积是（ ）。
17、一个直角三角板的两条直角边分别为a、b，以b为轴旋转一周，在你眼前出现一个（ ）体，a 是它的（ ），b是它的（ ）。
18、等底等高的圆柱和圆锥，已知圆柱的体积比圆锥多8立方分米，圆柱的体积是（ ），圆锥的体积是（ ）。
19、等底等体积的圆柱和圆锥，圆锥的高是6分米，圆柱的高是（ ）。
20、等高等体积的圆柱和圆锥，圆柱的底面积是3.14平方分米，圆锥的底面积是（ ）。
21、一个立方体的棱长扩大3倍，它的棱长总和扩大（ ）倍，底面积扩大（ ）倍，表面积扩大（ ）倍，体积扩大（ ）倍。
22、一个圆柱体的底面半径扩大4倍，高扩大5倍，它的底面直径扩大（ ）倍，周长扩大（ ）倍，底面积扩大（ ）倍，侧面积扩大（ ）倍，体积扩大（ ）倍。
23、一个长方体正好分割成3个形状、大小相等的正方体，这样增加的表面积相当于原长方体表面积的（ ）。
24、一台压路机的滚筒长1.5米，直径是6米。如果它每分钟转100圈，那么这种压路机每小时可以压路面（ ）平方米。
25．一根长5米的圆柱形木料，把它平均分成5段，表面积正好增加48平方分米，每段木料的体积是（ ）立方分米。
26．一个长方体仓库从里面量约长10米，宽5米，高6米，如果放入棱长是2米的正方体木箱，至多可以放进（ ）个。
27、将一个长12厘米，宽10厘米，高6厘米的长方体切成两个长方体，表面积最多增加（ ）平方厘米，最少增加（ ）平方厘米。
28、有一个用立方体木块搭成的立体图形：
从前面看是： 从左面看是：

要搭成这样的立体图形，至少需（ ）个立方体木块。
29、有一个长方体，正好可以切成大小相同的4个立方体，每个立方体的表面积是24平方厘米，原长方体的表面积可能是（ ）平方厘米，也可能是（ ）平方厘米。
30、（ ）个棱长是2厘米的立方体拼起来给成一个棱长是4厘米的立方体。
31、右图是由五个棱长2分米的立方体组成的图形，它的表面积是
（ ），体积是（ ）。
32、一个圆柱，沿着一条底面直径纵切后，可以得到一个边长8
厘米的正方形截面，这个圆柱的体积是（ ）。
一个酒精瓶，它的瓶身呈圆柱形(不包括瓶颈)，如图．已知它的容积为立方
厘米．当瓶子正放时，瓶内的酒精的液面高为6厘米；瓶子倒放时，空余部分的高为2
厘米．问：瓶内酒精的体积是多少立方厘米？合多少升？
【提高题】
1、 一个底面周长是6.28分米的圆柱形玻璃杯内盛有一些水，恰好占杯子容量的，现将两个同样大小的铁球沉入水中，这时水面上升了6厘米，刚好与杯口齐平．一个铁球的体积是多少立方厘米？