人教A版 (2019)5.4 三角函数的图象与性质教学设计

这是一份人教A版 (2019)5.4 三角函数的图象与性质教学设计，文件包含专题22三角函数的图象与性质正弦函数和余弦函数讲原卷版doc、专题22三角函数的图象与性质正弦函数和余弦函数讲解析版doc等2份教案配套教学资源，其中教案共33页， 欢迎下载使用。

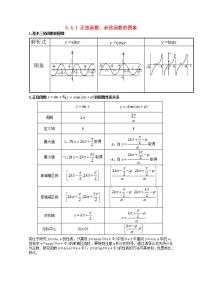
1．正、余弦函数解析式
2．正弦函数图象的画法
(1)几何法：利用正弦线画函数y＝sinx，x∈[0,2π]的图象，是把角x的正弦线向右平移，使它的起点与x轴上的点x重合，再用光滑的曲线把这些正弦线的终点连接起来，就得到函数y＝sinx，x∈[0,2π]的图象．
(2)五点法：用“五点法”作函数y＝sinx，x∈[0,2π]的图象的步骤是：
①列表：
②描点：在平面直角坐标系中描出五点：(0,0)， (eq \f(π,2)，1) ，(π，0)，(eq \f(3π,2)，－1)，(2π，0)．
③用光滑的曲线顺次连接这五个点，得正弦曲线在[0,2π]上的简图．
y＝sinx，x∈[0,2π]的图象向左、右平行移动(每次2π个单位长度)，就可以得到正弦函数y＝sinx，x∈R的图象．
3．正弦曲线、余弦曲线
(1)定义：正弦函数y＝sinx，x∈R和余弦函数y＝csx，x∈R的图象分别叫做正弦曲线和余弦曲线．
(2)图象：如图所示．
[知识点拨]1.函数y＝sinx，x∈[0,2π]与y＝sinx，x∈R的图象的关系
(1)函数y＝sinx，x∈[0,2π]的图象是函数y＝sinx，x∈R的图象的一部分．
(2)因为终边相同的角有相同的三角函数值，所以函数y＝sinx，x∈[2kπ，2(k＋1)π]，k∈Z且k≠0的图象与函数y＝sinx，x∈[0,2π]的图象形状完全一致，因此将y＝sinx，x∈[0,2π]的图象向左、右平行移动(每次移动2π个单位长度)，就可得到函数y＝sinx，x∈R的图象．
2．正弦曲线和余弦曲线的关系
eq \x(\a\al(y＝sinx，,x∈R的图象))eq \(,\s\up10(向左平移eq \f(π,2)个单位,向右平移\f(π,2)个单位))eq \x(\a\al(y＝csx，,x∈R的图象))
4．正弦函数、余弦函数的周期性和奇偶性
[知识点拨]1.对周期函数的两点说明
(1)并不是每一个函数都是周期函数，若函数具有周期性，则其周期也不一定唯一．
(2)在周期函数y＝f(x)中，若x∈D，则x＋nT∈D(x∈Z)．从而要求周期函数的定义域一定为无限集，且无上下界．
2．对函数最小正周期的两点说明
(1)最小正周期是指能使函数值重复出现的自变量x要加上的那个最小正数，这个正数是对x而言的，如y＝sin2x的最小正周期是π，因为y＝sin(2x＋2π)＝sin[2(x＋π)]，即π是使函数值重复出现的自变量x加上的最小正数，π是对x而言的，而非2x．
(2)并不是所有的周期函数都有最小正周期，譬如，常数函数f(x)＝c，任意一个正实数都是它的周期，因而不存在最小正周期．
3．正弦函数、余弦函数的奇偶性
(1)正弦函数是奇函数，余弦函数是偶函数，反映在图象上，正弦曲线关于原点O对称，余弦曲线关于y轴对称．
(2)正弦曲线、余弦曲线既是中心对称图形又是轴对称图形．
5．正弦函数的图象与性质
正弦函数的图象与性质如下表所示：
[拓展]正弦曲线是中心对称图形，其所有的对称中心坐标为(kπ，0)(k∈Z)，即正弦曲线与x轴的所有交点；正弦曲线也是轴对称图形，其所有的对称轴方程是x＝kπ＋eq \f(π,2)(k∈Z)，所有对称轴垂直于x轴，且与正弦曲线交点的纵坐标是正弦函数的最大(小)值．
6．余弦函数的图象与性质
余弦函数的图象与性质如下表所示：
[拓展]余弦曲线是中心对称图形，其所有的对称中心坐标是(kπ＋eq \f(π,2)，0)(k∈Z)，即余弦曲线与x轴的所有交点；余弦曲线也是轴对称图形，其所有的对称轴方程是x＝kπ(k∈Z)，所有对称轴垂直于x轴，且与余弦曲线交点的纵坐标是余弦函数的最大(小)值．
1．已知函数在区间上是单调函数，则实数a的最大值为 ．
2．若函数在区间（a，b）（0≤a＜b≤π）上单调递增，则b﹣a的最大值为 ．
3．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）＝cs3x+sin2x，则当x＜0时，f（x）的表达为 ．
4．函数y＝cs（2x）的单调递增区间是 ．
5．函数的最小值是 ．
重要考点一：用“五点法”作三角函数的图象
【典型例题】已知函数f（x）＝cs（2x）．
（1）求函数f（x）的单调递减区间．
（2）用“五点法”作出函数f（x）在[0，π]上的简图．
【题型强化】请用五点法作出函数在长度为一个周期上的大致图象．
【收官验收】设x∈R，函数f（x）＝cs（ωx+φ）（ω＞0，φ＜0）的最小正周期为π，且f（）．
（1）求ω和φ的值；
（2）在给定坐标系中作出函数f（x）在[0，π]上的图象；
（3）若f（x），求x的取值范围．
【名师点睛】
用“五点法”画函数y＝Asinx＋b(A≠0)或y＝Acsx＋b(A≠0)在[0,2π]上的简图的步骤：
(1)列表：
(2)描点：在平面直角坐标系中描出下列五个点：(0，y1)，(eq \f(π,2)，y2)，(π，y3)，(eq \f(3π,2)，y4)，(2π，y5)．
(3)连线：用光滑的曲线将描出的五个点连接起来．
重要考点二：利用图象变换作三角函数的图象
【典型例题】若将函数y＝sin2x的图象向左平移个单位长度，则平移后得到的函数图象的解析式为 ．
【题型强化】把函数y＝sinx图象上各点的横坐标缩短到原来的倍（纵坐标不变）得到函数，再向左平移个单位得到函数解析式是 ．
【收官验收】已知，曲线f（x）向左平移得曲线g（x），则g（x）的解析式为 ，f（x）+g（x）的最大值为 ．
【名师点睛】
函数的图象变换除了平移变换外，还有对称变换．如本例．一般地，函数f(x)的图象与f(－x)的图象关于y轴对称；－f(x)的图象与f(x)的图象关于x轴对称；－f(－x)的图象与f(x)的图象关于原点对称；f(|x|)的图象关于y轴对称．
重要考点三：利用正、余弦函数的图象解三角不等式
【典型例题】在[0，2π]上，满足sinx的取值范围是 ．
【题型强化】已知x满足sinx，则角x的取值范围为 ．
【收官验收】已知，则α的取值范围为 ；已知sinα＞csα，则α的取值范围为 ．
【名师点睛】
1.用三角函数的图象解sinx>a(或csx>a)的方法
(1)作出直线y＝a，作出y＝sinx(或y＝csx)的图象．
(2)确定sinx＝a(或csx＝a)的x值．
(3)确定sinx>a(或csx>a)的解集．
2．利用三角函数线解sinx>a(或csx>a)的方法
(1)找出使sinx＝a(或csx＝a)的两个x值的终边所在的位置．
(2)根据变化趋势，确定不等式的解集．
重要考点四：三角函数的周期
【典型例题】函数y＝sin的最小正周期为 ．
【题型强化】函数f（x）＝3cs（x）的最小正周期为 ．
【收官验收】已知函数f（x）＝sin（ωx+φ），（ω＞0）的部分图象如图所示，则f（x）的最小正周期为 ．
【名师点睛】
求三角函数周期的方法
(1)定义法：紧扣周期函数的定义，寻求对定义域内
的任意实数x都满足f(x＋T)＝f(x)的非零常数T.该方法主要适用于抽象函数．
(2)公式法：对形如y＝Asin(ωx＋φ)和y＝Acs(ωx＋φ)(其中A，ω，φ是常数，且A≠0，ω≠0)，可利用T＝eq \f(2π,|ω|)来求．
(3)图象法：可画出函数的图象，借助于图象判断函数的周期，特别是对于含绝对值的函数一般可采用此法．
重要考点五：三角函数奇偶性的判断
【典型例题】若函数y＝cs（x+φ）为奇函数，则最小的正数φ＝ ．
【题型强化】已知函数f（x）＝sin2（x+φ）（φ＞0）是偶函数，则φ的最小值是 ．
【收官验收】已知函数f（x）＝sin（ωx+φ）（ω＞0，φ∈R）是偶函数，点（1，0）是函数y＝f（x）图象的对称中心，则ω的最小值为 ．
【名师点睛】
1.判断函数奇偶性的常用方法：
(1)定义法，即从f(－x)的解析式中拼凑出f(x)的解析式，再看f(－x)＝－f(x)或f(－x)＝f(x)是否成立．
(2)图象法，即作出函数的图象，由图象的对称性确定其奇偶性．
(3)验证法，即验证f(－x)＋f(x)＝0或f(－x)－f(x)＝0(或eq \f(f－x,fx)＝±1)是否成立．此法通常用于函数是非奇非偶的情形．
2．判断函数奇偶性时，必须先判断其定义域是否关于原点对称．如果是，再验证f(－x)是否等于－f(x)或f(x)，进而再判断函数的奇偶性；如果不是，则该函数是非奇非偶数．
重要考点六：三角函数奇偶性与周期性的综合运用
【典型例题】已知函数f（x）＝cs（ωx+φ）（ω＞0，0＜φ＜π）图象关于原点对称，且其最小正周期为2，则ω＝ ，φ＝ ．
【题型强化】定义在R上的函数f（x）（x∈R）既是奇函数又是周期函数，若f（x）（x∈R）的最小正周期是π，且时f（x）＝sinx，则 ，方程f（x）＝0的解集为 ．
【收官验收】若，则f（1）+f（2）+f（3）+…+f（2017）＝ ．
【名师点睛】
1.解答此类题目的关键是利用化归的思想，借助于周期函数的定义把待求问题转化到已知区间上，代入求解即可．
2．如果一个函数是周期函数，若要研究该函数的有关性质，结合周期函数的定义可知，完全可以只研究该函数在一个周期上的特征，加以推广便可以得到该函数在其它义域内的有关性质．
重要考点七：三角函数的单调区间
【典型例题】已知函数．
（1）求y＝f（x）的单调减区间；
（2）当时，求f（x）的最大值和最小值．
【题型强化】已知函数．
（1）写出函数f（x）的单调递增区间；
（2）求函数f（x）在区间上的值域．
【收官验收】已知函数f（x）＝sin（2x）．
（Ⅰ）求f（）的值；
（Ⅱ）求f（x）的最小正周期；
（Ⅲ）求函数f（x）的单调递增区间．
【名师点睛】
求解与三角函数有关的函数的单调区间，主要利用换元法，将其转化为求正弦函数、余弦函数的单调区间，然后利用这两个函数的单调区间构造不等式，通过解不等式(组)即可得到所求函数的单调区间．
重要考点八：三角函数对称轴、对称中心
【典型例题】已知函数f（x）＝cs（2x+φ）（|φ|）的一个对称中心是（，0），则φ的值为 ．
【题型强化】若函数的图象在内恰有一条对称轴，则ω的最小值是 ．
【收官验收】已知曲线y＝sin（ωx）关于（﹣1，0）对称，则|ω|的最小值为 ．
【名师点睛】
求y＝Asin(ωx＋φ)或y＝Acs(ωx＋φ)函数的对称轴或对称中心时，应把ωx＋φ作为整体，代入相应的公式中，解出x的值，最后写出结果．
重要考点九：与三角函数有关的函数的值域(或最值)的求解问题
【典型例题】已知函数f（x）（sinx+csx）|sinx﹣csx|，则f（x）的值域是 ．
【题型强化】当时，函数y＝3﹣sinx﹣2cs2x的最小值是 ，最大值是 ．
【收官验收】函数的值域为 ．
【名师点睛】
1．求形如y＝asinx＋b的函数的最值或值域时，可利用正弦函数的有界性(－1≤sinx≤1)求解．
2．对于形如y＝Asin(ωx＋φ)＋k(Aω≠0)的函数，当定义域为R时，值域为[－|A|＋k，|A|＋k]；当定义域为某个给定的区间时，需确定ωx＋φ的范围，结合函数的单调性确定值域．
3．求形如y＝asin2x＋bsinx＋c，a≠0，x∈R的函数的值域或最值时，可以通过换元，令t＝sinx，将原函数转化为关于t的二次函数，利用配方法求值域或最值，求解过程中要注意正弦函数的有界性．
4．求形如y＝eq \f(asinx＋b,csinx＋d)，ac≠0的函数的值域，可以用分离常量法求解；也可以利用正弦函数的有界性建立关于y的不等式反解出y．
综上可知，求与三角函数有关的函数的值域(或最值)的常用方法有：(1)借助于正弦函数的有界性、单调性求解；
(2)转化为关于sinx的二次函数求解．注意求三角函数的最值对应的自变量x的值时，要考虑三角函数的周期性．
知识点课前预习与精讲精析
函数
解析式
定义域
正弦函数
y＝sinx
R
余弦函数
y＝csx
R
x
0
eq \f(π,2)
π
eq \f(3π,2)
2π
y＝sinx
0
1
0
－1
0
函数
y＝sinx
y＝csx
周期
2kπ(k∈Z且k≠0)
2kπ(k∈Z且k≠0)
最小正周期
2π
2π
奇偶性
奇函数
偶函数
解析式
y＝sinx
图象
定义域
R
当x＝ 2kπ＋eq \f(π,2)(k∈Z) 时，y取最大值1
值域
[－1，
1]
当x＝ 2kπ－eq \f(π,2)(k∈Z) 时，y取最小值1
最小正周期
2π
奇偶性
奇函数
单调性
在 eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2))) 上是增函数；
在 eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ＋\f(π,2)，2kπ＋\f(3π,2))) 上是减函数(k∈Z)
解析式
y＝csx
图象
定义域
R
当x＝ 2kπ(k∈Z) 时，y取最大值1
值域
[－1，
1]
当x＝ 2kπ＋π(k∈Z) 时，y取最小值1
最小正周期
2π
奇偶性
偶函数
单调性
在[(2kπ－1)π，2kπ]上是增函数；
在[2kπ，(2k＋1)π]上是减函数(k∈Z)
典型题型与解题方法
x
0
eq \f(π,2)
π
eq \f(3,2)π
2π
sinx或csx
0或1
1或0
0或－1
－1或0
0或1
y
y1
y2
y3
y4
y5