浙教版第六章 反比例函数综合与测试教学设计

这是一份浙教版第六章 反比例函数综合与测试教学设计，共15页。教案主要包含了反比例函数中的有关面积问题，利用k的几何意义进行面积转化，反比例函数中的直角三角形问题，反比例函数中的等腰三角形问题，反比例函数中的特殊四边形问题，反比例函数中的平行四边形问题，反比例函数中的不等式有关问题，反比例函数中的线段数量关系问题等内容，欢迎下载使用。

一、反比例函数的几何意义
1.反比例函数的几何意义：如图，在反比例函数图象上任选一点，向两坐标轴作垂线，垂线与坐标轴所围成矩形的面积为。如图二，所围成三角形的面积为

二、利用k的几何意义进行面积转化
1.如图，直线与反比例函数（）交于、两点，与、轴的交点分别为、，
那么，此方法是绝大部分学生选用的方法。但是，从效率来讲，就比较低
2.如图，过点、作轴的垂线，垂足分别为、，则根据的几何意义可得，，而，所以，此方法的好处，在于方便，快捷，不易出错。

1、如图，△BOD都是等腰直角三角形，过点B作AB⊥OB交反比例函数y＝（x＞0）于点A，过点A作AC⊥BD于点C，若S△BOD﹣S△ABC＝3，则k的值为 ．
2、如图，△OAC和△BAD都是等腰直角三角，∠ACO＝∠ADB＝90°，反比例函数y＝的图象经过点B，则△OAC与△BAD的面积之差S△OAC﹣S△BAD＝ ．
5、如图，直线y1＝k1x+b与双曲线y2＝在第一象限内交于A、B两点，已知A（1，m），B（2，1）．
（1）k1＝ ，k2＝ ，b＝ ．
（2）直接写出不等式y2＞y1的解集；
（3）设点P是线段AB上的一个动点，过点P作PD⊥x轴于点D，E是y轴上一点，求△PED的面积S的最大值．
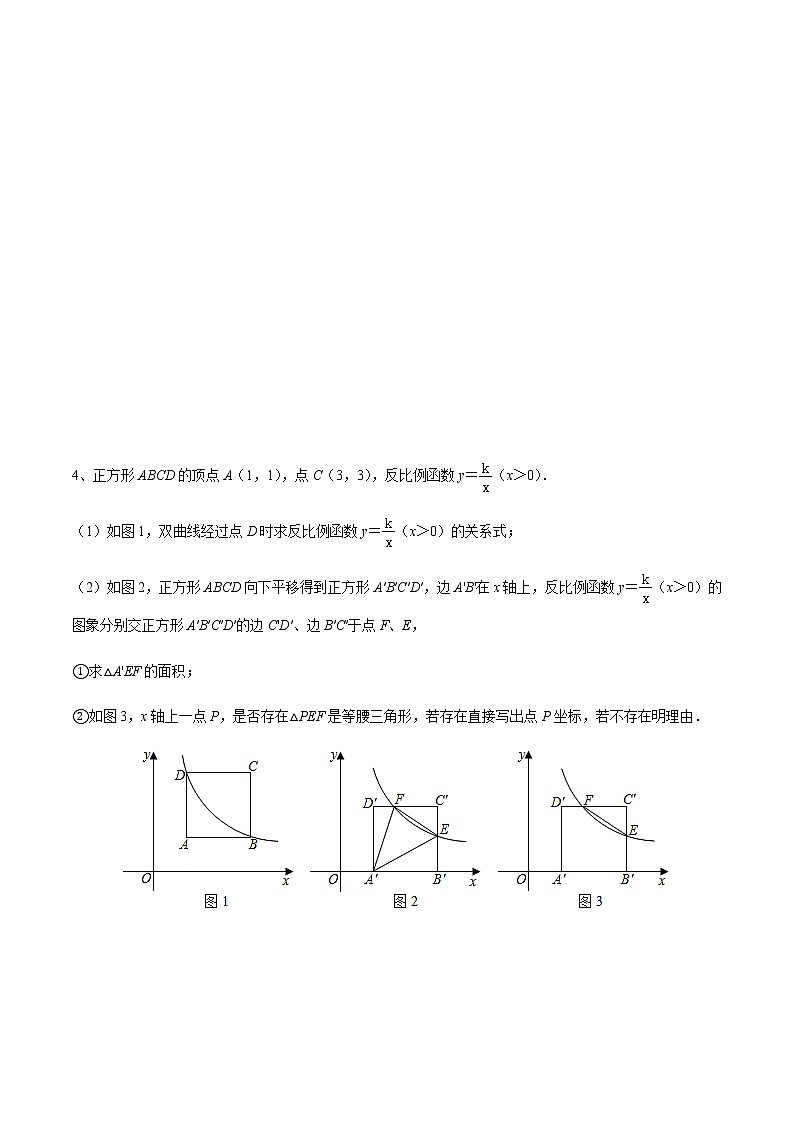
4、正方形ABCD的顶点A（1，1），点C（3，3），反比例函数y＝（x＞0）．
（1）如图1，双曲线经过点D时求反比例函数y＝（x＞0）的关系式；
（2）如图2，正方形ABCD向下平移得到正方形A′B′C′D′，边A'B'在x轴上，反比例函数y＝（x＞0）的图象分别交正方形A′B′C′D′的边C'D′、边B′C′于点F、E，
①求△A'EF的面积；
②如图3，x轴上一点P，是否存在△PEF是等腰三角形，若存在直接写出点P坐标，若不存在明理由．
12、如图，一次函数y＝﹣x+3的图象与反比例函数y＝（k≠0）在第一象限的图象交于A（1，a）和B两点，与x轴交于点C．
（1）求反比例函数的解析式；
（2）若点P在x轴上，且△APC的面积为5，求点P的坐标；
（3）若点P在y轴上，是否存在点P，使△ABP是以AB为一直角边的直角三角形？若存在，求出所有符合条件的P点坐标；若不存在，请说明理由．
题型二、反比例函数中的有关最值问题
一、k的几何意义与反比例函数对称性
1.如图一，直线与反比例函数（）交于、两点，与、轴的交点分别为、，
那么，此两种方法是绝大部分学生选用的方法。常规方法，费时、费力、而且还易计算出错。
2.如图二，我们知道反比例函数的图象是双曲线，关于原点成中心对称，那么延长交双曲线于点，连接、则，，因此可以将的面积转化为梯形的面积

1、如图，已知一次函数y＝x+2的图象分别与x轴、y轴交于点A、C与反比列函数y＝的图象在第一象限内交于点P，过点P作PB⊥x轴，垂足为B，且△ABP的面积为9．
（1）点A的坐标为 ，点C的坐标为 ，点P的坐标为 ；
（2）已知点Q在反比例函数y＝的图象上，其横坐标为6，在x轴上确定一点M使得△PQM的周长最小，求出点M的坐标．

2、如图，一次函数y＝kx+b的图象与反比例函数y＝（x＞0）的图象交于点P（n，2），与x轴交于点A（﹣4，0），与y轴交于点C，PB⊥x轴于点B，且AC＝BC．
（1）求一次函数、反比例函数的解析式；
（2）根据图象直接写出kx+b＜的x的取值范围；
（3）点D为反比例函数图象上使得四边形BCPD为菱形的一点，点E为y轴上的一动点，当|DE﹣PE|最大时，求点E的坐标．
3、菱形ABCD的顶点C与原点O重合，点B落在y轴正半轴上，点A、D落在第一象限内，且D点坐标为（4，3）．
（1）如图1，若反比例函数y＝（x＞0）的图象经过点A，求k的值；
（2）菱形ABCD向右平移t个单位得到菱形A1B1C1D1，如图2．
①请直接写出点B1、D1的坐标（用含t的代数式表示）：B1 、D1 ；
②是否存在反比例函数y＝（x＞0），使得点B1、D1同时落在y＝（x＞0）的图象上？若存在，求n的值；若不存在，请说明理由．
题型三、反比例函数中的直角三角形问题
1、如图，一次函数y＝kx+b（k≠0）与反比例函数y＝（a≠0）的图象在第一象限交于A，B两点，A点的坐标为（m，6），B点的坐标为（2，3），连接OA，过B作BC⊥y轴，垂足为C．
（1）求一次函数和反比例函数的表达式；
（2）在射线CB上是否存在一点D，使得△AOD是直角三角形，求出所有可能的D点坐标．
2、如图（1），正方形ABCD顶点A、B在函数y＝（k＞0）的图象上，点C、D分别在x轴、y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．
（1）若点A的横坐标为5，求点D的纵坐标；
（2）如图（2），当k＝8时，分别求出正方形A′B′C′D′的顶点A′、B′两点的坐标；
（3）当变化的正方形ABCD与（2）中的正方形A′B′C′D′有重叠部分时，求k的取值范围．
3、如图，如图，一次函数y＝﹣x+b与反比例函数的图象交于点A（m，1）和B （1，﹣3）．
（1）填空：一次函数的解析式为 ，反比例函数的解析式为 ；
（2）点P是x轴正半轴上一点，连接AP，BP．当△ABP是直角三角形时，求出点P的坐标．
题型四、反比例函数中的等腰三角形问题
1、如图所示，在平面直角坐标系中，一次函数y=kx+b(k≠0)与反比例函数y=(m≠0)的图象交于第二、四象限A、B两点，过点A作AD⊥x轴于D，AD=4，sin∠AOD=，且点B的坐标为(n,-2)．
（1）求一次函数与反比例函数的解析式；
（2）E是y轴上一点，且△AOE是等腰三角形，请直接写出所有符合条件的E点坐标．
2、如图，已知直线y＝﹣x+2分别与x轴，y轴交于A，B两点，与双曲线y＝交于E，F两点，若AB＝2EF，则k的值是 ．
题型五、反比例函数中的特殊四边形问题
1、如图，在直角坐标系xOy中，一直线y＝x+b经过点A（﹣3，0）与y轴正半轴交于B点，在x轴正半轴上有一点D，且OA＝OD，过D点作DC⊥x轴交直线y＝x+b于C点，反比例函数y＝（x＞0）经过点C．
（1）求这条直线和反比例函数的解析式；
（2）反比例函数图象上是否存在点P，使四边形BCPD为菱形？如果存在，求出P的点坐标；如果不存在，说明理由．
[
2、如图，直线y＝mx﹣1交y轴于点B，交x轴于点C，以BC为边的正方形ABCD的顶点A（﹣1，a）在双曲线y＝﹣（x＜0）上，D点在双曲线y＝（x＞0）上，则k的值为 ．
题型六、反比例函数中的平行四边形问题
1、如图，点A在双曲线y＝的第一象限的那一支上，AB垂直于y轴与点B，点C在x轴正半轴上，且OC＝2AB，点E在线段AC上，且AE＝3EC，点D为OB的中点，若△ADE的面积为3，则k的值为 ．
题型七、反比例函数中的不等式有关问题
1、如图①，直线y＝﹣x+b与反比例函数y＝（x＞0）的图象交于A（2，6），B（a，3）两点，BC∥x轴（点C在点B的右侧），且BC＝m，连接OC，过点C作CD⊥x轴于点D，交反比例函数图象于点E．
（1）求b的值和反比例函数的解析式；
（2）填空：不等式﹣x+b＞的解为 ；
（3）当OC平分∠BOD时，求的值；
（4）如图②，取BC中点F，连接DF，AF，BD，当四边形ABDF为平行四边形时，求点F的坐标．
题型八、反比例函数中的线段数量关系问题
1、如图，在平面直角坐标系中，矩形OABC的边BC交x轴于点D，AD⊥x轴，反比例函数y＝（x＞0）的图象经过点A，点D的坐标为（3，0），AB＝BD．
（1）求反比例函数的解析式；
（2）点P为y轴上一动点，当PA+PB的值最小时，求出点P的坐标．

题型九、反比例函数中的几何图形存在性问题
1、如图所示，在平面直角坐标系中，一次函数y＝kx+b（k≠0）与反比例函数y＝（m≠0）的图象交于第二、四象限A、B两点，过点A作AD⊥x轴于D，AD＝4，sin∠AOD＝，且点B的坐标为（n，﹣2）．
（1）求一次函数与反比例函数的解析式；
（2）E是y轴上一点，且△AOE是等腰三角形，请直接写出所有符合条件的E点坐标．

题型十、反比例函数综合
1．如图，在平面直角坐标系中，直线y＝与x轴，y轴分别相交于A，B两点，与反比例函数y＝（x＞0）的图象交于点C，点C的横坐标为4．
（1）求k的值；
（2）过点C作CD⊥y轴，垂足为D，点E是该反比例函数y＝（x＞0）的图象上一点，连接ED，EC，且ED＝EC；
①求点E的坐标；
②求点E到直线y＝的距离d的值．
2．如图，在平面直角坐标系中，一次函数y＝kx+b（k≠0）的图象与反比例函数y＝（m≠0）的图象交于第二、四象限内的A、B两点，与y轴交于点C，过点A作AM⊥x轴，垂足为M，OA＝4，cs∠AOM＝，点B的横坐标为．
（1）求该反比例函数和一次函数的解析式；
（2）连接MC，在x轴上找一点P，使△PMC的面积与四边形AMCO的面积相等，求P的坐标．