高中数学人教A版 (2019)选择性必修 第三册6.1 分类加法计数原理与分步乘法计数原理复习ppt课件

这是一份高中数学人教A版 (2019)选择性必修 第三册6.1 分类加法计数原理与分步乘法计数原理复习ppt课件，共22页。PPT课件主要包含了一知识复习，二项式定理，二项式系数的性质，各二项式系数和，二典型例题，题型一排列问题，方法小结，题型二组合问题，题型三分组分配问题，分组分配问题等内容，欢迎下载使用。
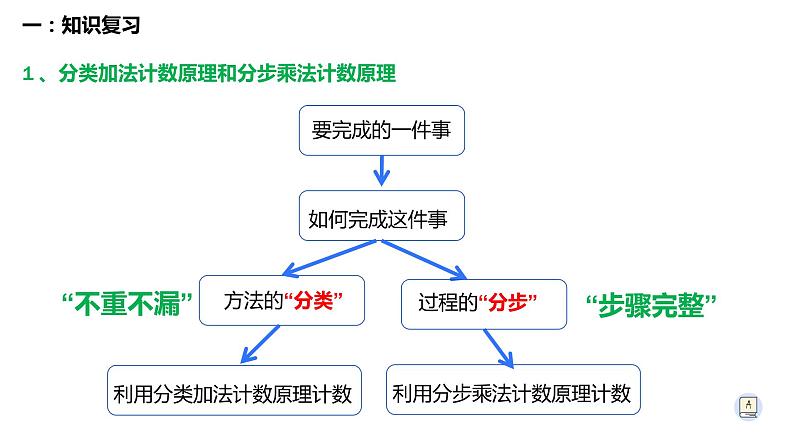
1 、分类加法计数原理和分步乘法计数原理
2、排列数、组合数的公式及性质
(1)展开式共有 n+1 项．
【例1】有3名男生、4名女生，在下列不同条件下，求不同的排列方法总数.(1)选5人排成一排；(2)排成前后两排，前排3人，后排4人；(3)全体排成一排，甲不站排头也不站排尾；(4)全体排成一排，女生必须站在一起；(5)全体排成一排，男生互不相邻.
求解排列问题的6种主要方法
【例2】某市工商局对35种商品进行抽样检查，已知其中有15种假货.现从35种商品中选取3种.(1)其中某一种假货必须在内，不同取法有多少种？(2)其中某一种假货不能在内，不同取法有多少种？(3)恰有2种假货在内，不同取法有多少种？(4)至少有2种假货在内，不同取法有多少种？(5)至多有2种假货在内，不同取法有多少种？
组合问题的2类题型及求解方法
(1)“含有”或“不含有”某些元素的组合题型：“含”，则先将这些元素取出，再由另外的元素补足；“不含”，则先将这些元素剔除，再从剩下的元素中去选取.(2)“至少”或“至多”含有几个元素的组合题型：解这类题必须十分重视“至少”与“至多”这两个关键词的含义，谨防重复与漏解.用直接法和间接法都可以求解，通常用直接法分类复杂时，考虑逆向思维，用间接法处理.
【例3】六本不同的书，按下列要求各有多少种不同的分法？ （1） 分给甲、乙、丙三人，甲得一本，乙得两本，丙得三本；（2） 分给甲、乙、丙三人，每人两本；（3） 分给甲、乙、丙三人，甲得四本，乙得一本，丙得一本；（4）分为三份，一份一本，一份两本，一份三本；（5）分为三份，每份两本；（6）分为三份，一份四本，一份一本，一份一本；（7）分给甲、乙、丙三人，一人一本，一人两本，一人三本；（8）分给甲、乙、丙三人，一人得四本，另外两个人每个人得一本；（9）分给甲、乙、丙三人，每人至少一本.
(1)完全平均分组：在分组时，每组元素的个数都相等.　①只分组无分配时，需要除以这几组的“全排列”，以确保消去重复；　②分组且分配时，一种方法是先分组再分配；另一种方法是可以用分步乘法 计数原理解题.(2)部分平均分组：在分组时，每组的个数是不均等的，而是有一部分个数相同． 需要除以相同的组的“全排列”，保证没有重复．(3)非平均分组：每组所要分的元素个数是不相同的．这种分组不考虑重复现象。
解题思想：先分组、后分配
【例4】现用五种不同的颜色，要对如图中的四个部分进行着色，要求公共边的两块不能用同一种颜色，共有__________种不同着色方法 .
【例5】某龙舟队有9名队员，其中3人只会划左舷，4人只会划右舷，2人既会划左舷又会划右舷．现要选派划左舷的3人、右舷的3人共6人去参加比赛，则不同的选派方法共有   A.56种B. 68种C. 74种D. 92种
题型六：求展开式中指定的项或某一项的系数或二项式系数
(1)求展开式中的特定项.可依据条件写出第r＋1项，再由特定项的特点求出r值即可.(2)已知展开式的某项，求特定项的系数.可由某项得出参数项，再由通项写出第r＋1项，由特定项得出r值，最后求出其参数.
求二项展开式有关问题的方法
题型七：二项式系数的性质与各项系数和