冀教版八年级上册13.3 全等三角形的判定图片ppt课件

这是一份冀教版八年级上册13.3 全等三角形的判定图片ppt课件，共14页。PPT课件主要包含了学习目标，知识回顾，SSS，SAS，ASA，AAS，BCEF，ABDE，∠A∠D，探究与思考等内容，欢迎下载使用。
3、培养学生学习事物的特殊、一般关系、发展逻辑思维能力。
1、掌握直角三角形全等的判定方法：“斜边、直角边”；
2、经历探索直角三角形全等条件的过程，体会一般与特殊的辨证关系；
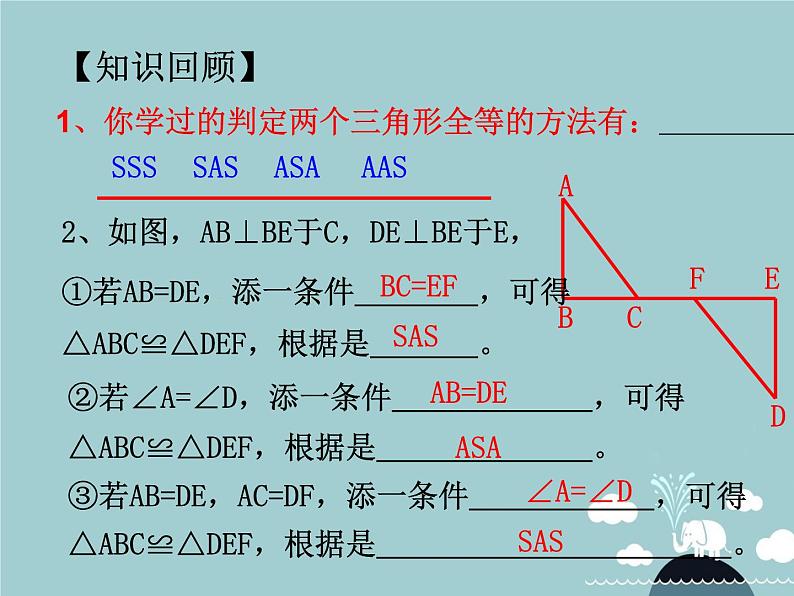
2、如图，AB⊥BE于C，DE⊥BE于E，
①若AB=DE，添一条件 ，可得△ABC≌△DEF，根据是 。
②若∠A=∠D，添一条件 ，可得△ABC≌△DEF，根据是 。
③若AB=DE，AC=DF，添一条件 ，可得△ABC≌△DEF，根据是 。
阅读课本，完成以下内容：
已知线段a =3cm，c=5cm，作一个Rt△ABC，使∠C=90°，AB=c，CB=a
(1)按步骤作图：①作∠MCN=90°；②在射线CM上截取线段CB=a；③以B为圆心，C为半径画弧，交射线CN于点A； ④连结AB得△ABC。
(2)把你画的△ABC剪下与同伴画的三角形进行比较,它们全等吗？
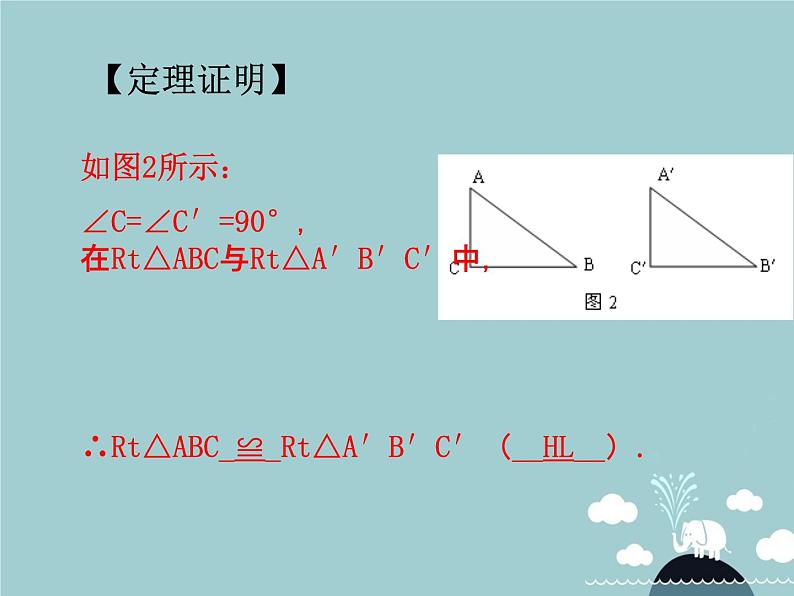
∠C=∠C′=90°，在Rt△ABC与Rt△A′B′C′中，
∴Rt△ABC_≌_Rt△A′B′C′（__HL__）.
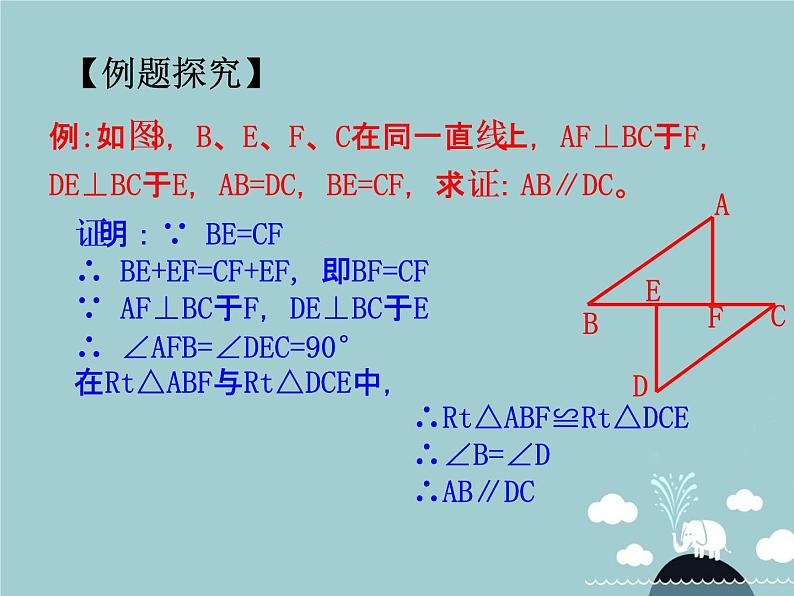
例:如图3，B、E、F、C在同一直线上，AF⊥BC于F，DE⊥BC于E，AB=DC，BE=CF，求证：AB∥DC。
分析：由BE=CF得到BF=CE，进而利用“HL”证明△ABF≌△DCE,再由两三角形全等得到∠B=∠C，所以AB∥DC。
证明：∵ BE=CF∴ BE+EF=CF+EF, 即BF=CF∵ AF⊥BC于F，DE⊥BC于E∴ ∠AFB=∠DEC=90°在Rt△ABF与Rt△DCE中，
∴Rt△ABF≌Rt△DCE∴∠B=∠D∴AB∥DC
1、判断两个直角三角形全等的方法不正确的有（ ）A、两条直角边对应相等 B、斜边和一锐角对应相等C、斜边和一条直角边对应相等 D、两个锐角对应相等
3、如图，CE⊥AB，DF⊥AB，垂足分别为E、F，

4、如图，已知AE=DE，AE⊥DE，AB⊥BC，DC⊥BC.求证：AB＋CD=BC.
分析：欲证AB＋CD＝BC，只须证明△ABE≌△DCE即可.
证明：∵AB⊥BC，DC⊥BC∴∠ABE=∠DCE=90°又∵AE⊥DE∴∠AED=90°即：∠AEB+∠DEC=90°∵∠CDE+∠DEC=90°∴∠AEB=∠CDE在△ABE和△DCE中
∴△ABE≌△DCE∴AB=EC，BE=CD∴AB+CD=BE+EC=BC.
5、如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系？并说明理由。
解：在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF∴∠ABC=∠DFE.