高中数学人教版新课标A选修1-1第三章 导数及其应用综合与测试测试题

这是一份高中数学人教版新课标A选修1-1第三章 导数及其应用综合与测试测试题，共4页。
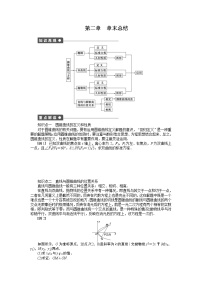
第三章  章末总结  知识点一　导数与曲线的切线利用导数的几何意义求切线方程时关键是搞清所给的点是不是切点，常见的类型有两种，一类是求“在某点处的切线方程”，则此点一定为切点，先求导，再求斜率代入直线方程即可得；另一类是求“过某点的切线方程”，这种类型中的点不一定是切点，可先设切点为Q(x1，y1)，则切线方程为y－y1＝f′(x1)(x－x1)，再由切线过点P(x0，y0)得y0－y1＝f′(x1)(x0－x1)          ①又y1＝f(x1)                    ②由①②求出x1，y1的值．即求出了过点P(x0，y0)的切线方程．例1　已知曲线f(x)＝x3－3x，过点A(0,16)作曲线f(x)的切线，求曲线的切线方程．  知识点二　导数与函数的单调性利用导数研究函数的单调区间是导数的主要应用之一，其步骤为：(1)求导数f′(x)；(2)解不等式f′(x)>0或f′(x)<0；(3)确定并指出函数的单调增区间、减区间．特别要注意写单调区间时，区间之间用“和”或“，”隔开，绝对不能用“∪”连接．例2　求下列函数的单调区间：(1)f(x)＝＋sin x；(2)f(x)＝x(x－a)2.         知识点三　导数与函数的极值、最值利用导数研究函数的极值和最值是导数的另一主要应用．1．应用导数求函数极值的一般步骤：(1)确定函数f(x)的定义域；(2)解方程f′(x)＝0的根；(3)检验f′(x)＝0的根的两侧f′(x)的符号．若左正右负，则f(x)在此根处取得极大值；若左负右正，则f(x)在此根处取得极小值；否则，此根不是f(x)的极值点．2．求函数f(x)在闭区间[a，b]上的最大值、最小值的方法与步骤：(1)求f(x)在(a，b)内的极值；(2)将(1)求得的极值与f(a)、f(b)相比较，其中最大的一个值为最大值，最小的一个值为最小值；特别地，①当f(x)在(a，b)上单调时，其最小值、最大值在区间端点处取得，②当f(x)在(a，b)内只有一个极值点时，若在这一点处f(x)有极大(小)值，则可以断定f(x)在该点处取得最大(小)值，这里(a，b)也可以是(－∞，＋∞)．例3　设<a<1，函数f(x)＝x3－ax2＋b (－1≤x≤1)的最大值为1，最小值为－，求常数a，b.     知识点四　导数与参数的范围已知函数的单调性求参数的取值范围时，可以有两种方法：一是利用函数单调性的定义，二是利用导数法．利用导数法更为简捷．在解决问题的过程中主要处理好等号的问题，因为f′(x)>0(或f′(x)<0)仅是一个函数在某区间上递增(或递减)的充分不必要条件，而其充要条件是：f′(x)≥0(或f′(x)≤0)，且f′(x)不恒为零．利用导数法解决取值范围问题时可以有两个基本思路：一是将问题转化为不等式在某区间上的恒成立问题，即f′(x)≥0或f′(x)≤0恒成立，用分离参数或函数性质求解参数范围，然后检验参数取“＝”时是否满足题意；另一思路是先令f′(x)>0(或f′(x)<0)，求出参数的取值范围后，再令参数取“＝”，看此时f(x)是否满足题意．例4　已知函数f(x)＝x2＋ (x≠0，常数a∈R)．若函数f(x)在x∈[2，＋∞)上是单调递增的，求a的取值范围．           例5　已知f(x)＝x3－x2－2x＋5，当x∈[－1,2]时，f(x)<m恒成立，求实数m的取值范围．   章末总结  答案重点解读例1　解　设切点为(x0，y0)，则由导数定义得切线的斜率k＝f′(x0)＝3x－3，∴切线方程为y＝(3x－3)x＋16，又切点(x0，y0)在切线上，∴y0＝3(x－1)x0＋16，即x－3x0＝3(x－1)x0＋16，解得x0＝－2，∴切线方程为9x－y＋16＝0.例2　解　(1)函数的定义域是R，f′(x)＝＋cos x，令＋cos x>0，解得2kπ－<x<2kπ＋ (k∈Z)，令＋cos x<0，解得2kπ＋<x<2kπ＋ (k∈Z)，因此，f(x)的单调增区间是 (k∈Z)，单调减区间是 (k∈Z)．(2)函数f(x)＝x(x－a)2＝x3－2ax2＋a2x的定义域为R，由f′(x)＝3x2－4ax＋a2＝0，得x1＝，x2＝a.①当a>0时，x1<x2.∴函数f(x)的单调递增区间为，(a，＋∞)，单调递减区间为.②当a<0时，x1>x2，∴函数f(x)的单调递增区间为(－∞，a)，，单调递减区间为.③当a＝0时，f′(x)＝3x2≥0，∴函数f(x)的单调区间为(－∞，＋∞)，即f(x)在R上是增加的．例3　解　令f′(x)＝3x2－3ax＝0，得x1＝0，x2＝a.当x变化时，f′(x)与f(x)的变化情况如下表：x－1(－1,0)0(0，a)a(a,1)1f′(x) ＋0－0＋ f(x)－1－a＋b b  －＋b 1－a＋b从上表可知，当x＝0时，f(x)取得极大值b，而f(0)>f(a)，f(1)>f(－1)，故需比较f(0)与f(1)的大小．因为f(0)－f(1)＝a－1>0，所以f(x)的最大值为f(0)＝b.所以b＝1.又f(－1)－f(a)＝(a＋1)2(a－2)<0，所以f(x)的最小值为f(－1)＝－1－a＋b＝－a，所以－a＝－，所以a＝.例4　解　f′(x)＝2x－＝.要使f(x)在[2，＋∞)上是单调递增的，则f′(x)≥0在x∈[2，＋∞)上恒成立，即≥0在x∈[2，＋∞)上恒成立．∵x2>0，∴2x3－a≥0，∴a≤2x3在x∈[2，＋∞)上恒成立．∴a≤(2x3)min.∵x∈[2，＋∞)，y＝2x3是单调递增的，∴(2x3)min＝16，∴a≤16.当a＝16时，f′(x)＝≥0 (x∈[2，＋∞))有且只有f′(2)＝0，∴a的取值范围是a≤16.例5　解　∵f(x)＝x3－x2－2x＋5，∴f′(x)＝3x2－x－2.令f′(x)＝0，即3x2－x－2＝0，∴x＝1或x＝－.当x∈时，f′(x)>0，f(x)为增函数；当x∈时，f′(x)<0，f(x)为减函数；当x∈(1,2)时，f′(x)>0，f(x)为增函数．所以，当x＝－时，f(x)取得极大值f＝；当x＝1时，f(x)取得极小值f(1)＝.又f(－1)＝，f(2)＝7，因此，f(x)在[－1,2]上的最大值为f(2)＝7.要使f(x)<m恒成立，需f(x)max<m，即m>7.所以，所求实数m的取值范围是(7，＋∞)．