初中数学人教版八年级上册11.1.1 三角形的边习题

这是一份初中数学人教版八年级上册11.1.1 三角形的边习题，共8页。试卷主要包含了1 与三角形有关的线段等内容，欢迎下载使用。
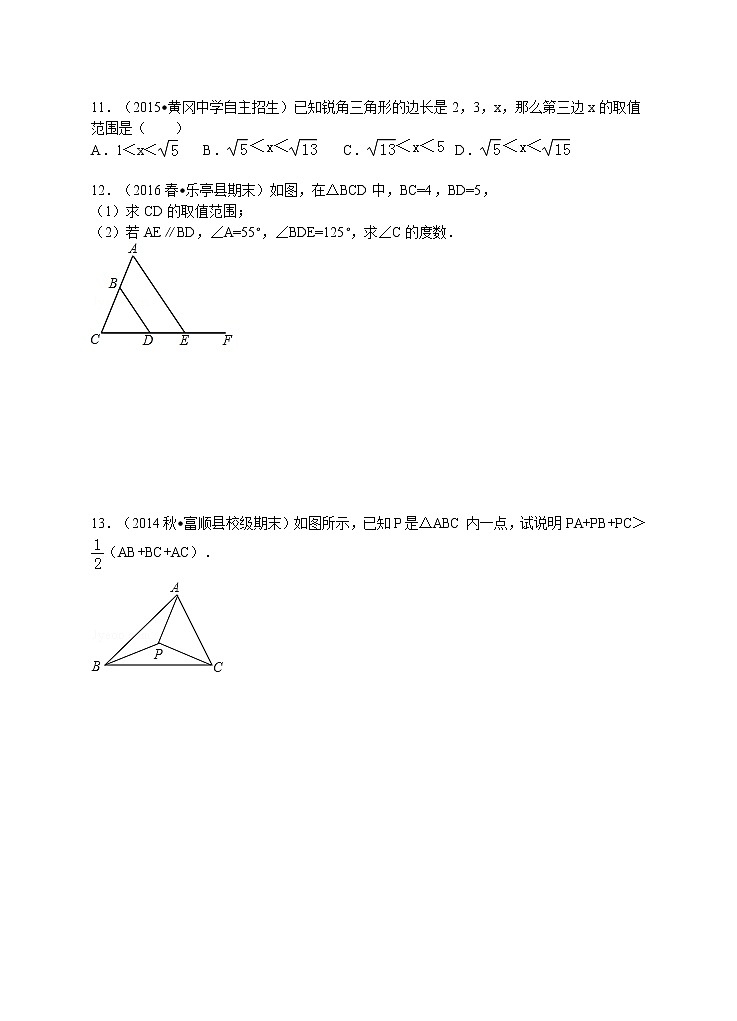
第十一章    三角形11.1    与三角形有关的线段11.1.1    三角形的边 一、基础题训练1．（2015•南通）下列长度的三条线段能组成三角形的是（　　）A．5，6，10 B．5，6，11 C．3，4，8 D．4a，4a，8a（a＞0） 2．（2015•青海）已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（　　）A．5 B．6 C．12 D．16 3．（2016•端州区一模）已知三角形的两边长分别为3和6，那么第三边长的取值范围是　　　　　　． 4．（2016春•枣庄校级月考）如果三角形的三边长度分别为3a、4a、14，则a的取值范围是　　　　　　． 5．（2016•西宁）下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（　　）A．3cm，4cm，8cm B．8cm，7cm，15cmC．5cm，5cm，11cm D．13cm，12cm，20cm 6．（2015•朝阳）一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为　　　　　　． 7．（2016•长沙）若一个三角形的两边长分别为3和7，则第三边长可能是（　　）A．6 B．3 C．2 D．11．8．（2015春•太康县期末）在△ABC中，AB=9，AC=2，并且BC的长为偶数，求△ABC的周长     二、中档题训练9．（2015•佛山）各边长度都是整数、最大边长为8的三角形共有　　　　　　个． 10．（2016春•江都区校级月考）已知a、b、c为△ABC的三边，则化简|a+b+c|﹣|a﹣b﹣c|﹣|a﹣b+c|﹣|a+b﹣c|=　　　　　　． 11．（2015•黄冈中学自主招生）已知锐角三角形的边长是2，3，x，那么第三边x的取值范围是（　　）A．1＜x＜ B． C． D． 12．（2016春•乐亭县期末）如图，在△BCD中，BC=4，BD=5，（1）求CD的取值范围；（2）若AE∥BD，∠A=55°，∠BDE=125°，求∠C的度数．        13．（2014秋•富顺县校级期末）如图所示，已知P是△ABC内一点，试说明PA+PB+PC＞（AB+BC+AC）．             三、综合题训练14．（2015春•宜阳县期末）已知三角形的三条边为互不相等的整数，且有两边长分别为7和9，另一条边长为偶数．（1）请写出一个三角形，符合上述条件的第三边长．（2）若符合上述条件的三角形共有a个，求a的值．            15．（2014春•苏州期末）观察并探求下列各问题，写出你所观察得到的结论，并说明理由．（1）如图，△ABC中，P为边BC上一点，试观察比较BP+PC与AB+AC的大小，并说明理由．      （2）将（1）中点P移至△ABC内，得图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由．  （3）将（2）中点P变为两个点P1、P2得下图，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．    （4）将（3）中的点P1、P2移至△ABC外，并使点P1、P2与点A在边BC的异侧，且∠P1BC＜∠ABC，∠P2CB＜∠ACB，得图，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．　　    （5）若将（3）中的四边形BP1P2C的顶点B、C移至△ABC内，得四边形B1P1P2C1，如图⑤，试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小，并说明理由．    2．（2015•青海）已知三角形两边的长分别是4和10，则此三角形第三边的长可能是（　　）A．5 B．6 C．12 D．16【考点】三角形三边关系．21世纪教育网【分析】设第三边的长为x，再由三角形的三边关系即可得出结论．【解答】解：设第三边的长为x，∵三角形两边的长分别是4和10，∴10﹣4＜x＜10+4，即6＜x＜14．故选C．【点评】本题考查的是三角形的三边关系，熟知三角形任意两边之和大于第三边，任意两边之差小于第三边是解答此题的关键． 4．（2016春•枣庄校级月考）如果三角形的三边长度分别为3a、4a、14，则a的取值范围是　2＜a＜14　．【考点】三角形三边关系．21世纪教育网【分析】根据三角形的三边关系“任意两边之和＞第三边，任意两边之差＜第三边”，列不等式组求解．  【解答】解：根据三角形的三边关系，得，解得2＜a＜14．【点评】此题要能够根据三角形的三边关系列不等式组，熟练解不等式组． 6．（2015•朝阳）一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为　8　．【考点】三角形三边关系．21世纪教育网【分析】首先设第三边长为x，根据三角形的三边关系可得3﹣2＜x＜3+2，然后再确定x的值，进而可得周长．【解答】解：设第三边长为x，∵两边长分别是2和3，∴3﹣2＜x＜3+2，即：1＜x＜5，∵第三边长为奇数，∴x=3，∴这个三角形的周长为2+3+3=8，故答案为：8．【点评】此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边，三角形的两边差小于第三边． 【点评】本题考查三角形三边关系定理，记住两边之和第三边，两边之差小于第三边，属于基础题，中考常考题型． 9．（2015•佛山）各边长度都是整数、最大边长为8的三角形共有　20　个．【考点】三角形三边关系．21世纪教育网【分析】利用三角形三边关系进而得出符合题意的答案即可．【解答】解：∵各边长度都是整数、最大边长为8，∴三边长可以为：1，8，8；2，7，8；2，8，8；3，6，8；3，7，8；3，8，8；4，5，8；4，6，8；4，7，8；4，8，8；5，5，8；5，6，8；5，7，8；5，8，8；6，6，8；6，7，8；6，8，8；7，7，8；7，8，8；8，8，8；故各边长度都是整数、最大边长为8的三角形共有20个．故答案为：20．【点评】此题主要考查了三角形三边关系，正确分类讨论得出是解题关键．  12．（2016春•乐亭县期末）如图，在△BCD中，BC=4，BD=5，（1）求CD的取值范围；（2）若AE∥BD，∠A=55°，∠BDE=125°，求∠C的度数．【考点】三角形三边关系；平行线的性质．21世纪教育网【分析】（1）利用三角形三边关系得出DC的取值范围即可；（2）利用平行线的性质得出∠AEC的度数，再利用三角形内角和定理得出答案．【解答】解：（1）∵在△BCD中，BC=4，BD=5，∴1＜DC＜9； （2）∵AE∥BD，∠BDE=125°，∴∠AEC=55°，又∵∠A=55°，∴∠C=70°．【点评】此题主要考查了三角形三边关系以及平行线的性质，得出∠AEC的度数是解题关键．  【解答】证明：在△ABP中：AP+BP＞AB．同理：BP+PC＞BC，AP+PC＞AC．以上三式分别相加得到：2（PA+PB+PC）＞AB+BC+AC，即PA+PB+PC＞（AB+BC+AC）．【点评】解本题的本题的关键是多次运用了三角形的三边关系定理． 15．（2014春•苏州期末）观察并探求下列各问题，写出你所观察得到的结论，并说明理由．（1）如图，△ABC中，P为边BC上一点，试观察比较BP+PC与AB+AC的大小，并说明理由．（2）将（1）中点P移至△ABC内，得图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由．（3）将（2）中点P变为两个点P1、P2得下图，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．（4）将（3）中的点P1、P2移至△ABC外，并使点P1、P2与点A在边BC的异侧，且∠P1BC＜∠ABC，∠P2CB＜∠ACB，得图，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．（5）若将（3）中的四边形BP1P2C的顶点B、C移至△ABC内，得四边形B1P1P2C1，如图⑤，试观察比较四边形B1P1P2C1的周长与△ABC的周长的大小，并说明理由． （3）四边形BP1P2C的周长＜△ABC的周长．理由：