高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式图片课件ppt

这是一份高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式图片课件ppt，共23页。PPT课件主要包含了跟踪训练二等内容，欢迎下载使用。
1.掌握基本不等式的形式以及推导过程，会用基本不等式解决简单问题。2.经历基本不等式的推导与证明过程，提升逻辑推理能力。3.在猜想论证的过程中，体会数学的严谨性。
1.数学抽象：基本不等式的形式以及推导过程；2.逻辑推理：基本不等式的证明；3.数学运算：利用基本不等式求最值；4.数据分析：利用基本不等式解决实际问题；5.数学建模：利用函数的思想和基本不等式解决实际问题，提升学生的逻辑推理能力。
阅读课本44-45页，思考并完成以下问题1. 重要不等式的内容是？2.基本不等式的内容及注意事项？3.常见的不等式推论？要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。
2.基本不等式 (1)基本不等式成立的条件:____________.(2)等号成立的条件:当且仅当______时取等号.
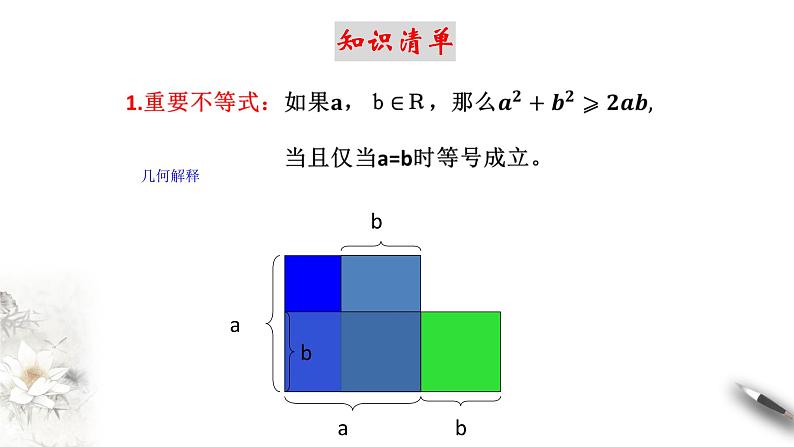
3.几个重要的不等式 (1)a2+b2≥ _______(a,b∈R). (2) ≥____(a,b同号). (3) (a,b∈R). (4) (a,b∈R).4.算术平均数与几何平均数 设a>0,b>0，则a,b的算术平均数为 ,几何平均 数为______，基本不等式可叙述为：_____________ ________________________________.
术平均数不小于它们的几何平均数
题型分析 举一反三
题型一利用基本不等式求最值
求下列各题的最值.（1）已知x>0,y>0,xy=10,求 的最小值；（2）x>0,求 的最小值；（3）x0,y>0,xy=10.当且仅当2y=5x,即x=2,y=5时等号成立.
(2)∵x>0, 等号成立的条件是 即x=2,∴f(x)的最小值是12.
(3)∵x0,y>0，且 求x+y 的最小值；（2）已知x< 求函数 的最大值;（3）若x,y∈(0,+∞)且2x+8y-xy=0,求x+y的最小值.
解（1）∵x>0,y>0, 当且仅当 时，上式等号成立，∴x=4,y=12时，(x+y)min=16.
(2)∵x< ∴5-4x>0,≤-2+3=1,当且仅当 即x=1时，上式等号成立，故当x=1时，ymax=1.
(3)由2x+8y-xy=0,得2x+8y=xy,当且仅当 即x=2y时取等号，又2x+8y-xy=0,∴x=12,y=6,∴当x=12,y=6时，x+y取最小值18.
题型二利用基本不等式解决实际问题
解题方法（利用基本不等式解决实际问题）
设出未知数x,y,根据已知条件，列出关系式，然后利用函数的思想或基本不等式解决相应的问题。（注意运用基本不等式讲究“一正二定三等”）