






高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用教课内容课件ppt
展开1.理解直线和平面垂直的性质定理并能运用其解决相关问题.2.通过对空间距离的理解和应用,培养学生的空间转化能力和逻辑推理能力.
1.逻辑推理:探究归纳直线和平面垂直的性质定理,线线垂直与线面垂直转化;2.数学运算:求空间点面、线面、面面距离.3.直观想象:题中几何体的点、线、面的位置关系.
阅读课本153-155页,思考并完成以下问题1、垂直与同一条直线的两条直线有什么位置关系?2、与线面垂直有关的结论有哪些?3、怎样定义直线与平面的距离、平面与平面的距离? 要求:学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
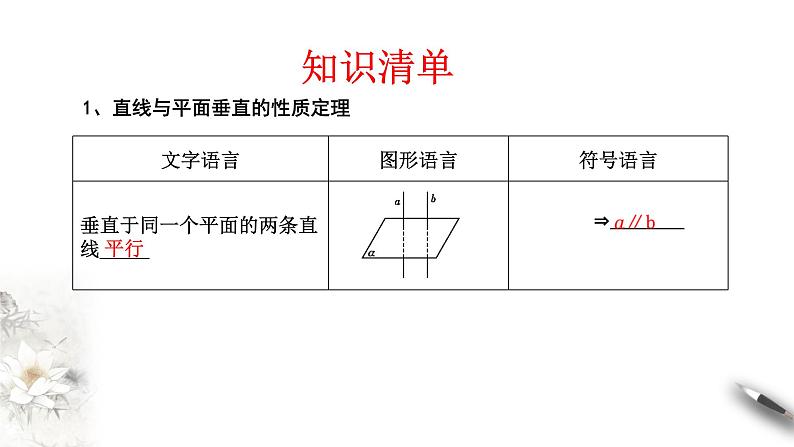
1、直线与平面垂直的性质定理
2、距离(1)直线与平面的距离:一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离.(2)平面与平面的距离:两个平面平行时,其中一个平面内任意一点到另一个平面的距离.
1.在正方体ABCD-A1B1C1D1中,直线l⊥平面A1C1(l与棱不重合),则( )A.B1B⊥l B.B1B∥lC.B1B与l异面D.B1B与l相交
2.已知a,b为两条不同的直线,α,β为两个不同的平面,下列四个命题:①a∥b,a∥α⇒b∥α;②a⊥b,a⊥α⇒b∥α;③a∥α,β∥α⇒a∥β;④a⊥α,β⊥α⇒a∥β.其中不正确的有( )A.1个B.2个C.3个D.4个
3.如果直线l,m与平面α,β,γ之间满足:l=β∩γ,l∥α,m⊂α和m⊥γ,那么( )A.α⊥γ且l⊥m B.α⊥γ且m∥βC.m∥β且l⊥m D.α∥β且α⊥γ
4.线段AB在平面α的同侧,A,B到α的距离分别为3和5,则AB的中点到α的距离为________.
题型分析 举一反三
例1 如图所示,在正方体ABCD-A1B1C1D1中,M是AB上的一点,N是A1C的中点, MN⊥平面A1DC.求证:(1)MN∥AD1;(2)M是AB的中点.
解题技巧(证明两条直线平行的常见方法)
证明 因为EB⊥β,a⊂β,所以EB⊥a.又因为a⊥AB,AB∩EB=B,所以a⊥平面ABE.因为α∩β=l,所以l⊂α,l⊂β.因为EA⊥α,EB⊥β,所以EA⊥l,EB⊥l.又因为EA∩EB=E,所以l⊥平面ABE.所以a∥l.
例2 如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.若AE=A1E,AB=3,求四棱锥E-BB1C1C的体积.
解题技巧(空间中距离的转化)
1、如图,四棱锥P-ABCD中,PA⊥菱形ABCD所在的平面,∠ABC=60°,E是BC的中点,M是PD的中点.(1)求证:AE⊥平面PAD.(2)若AB=AP=2,求三棱锥P-ACM的体积.
人教A版 (2019)8.6 空间直线、平面的垂直课堂教学ppt课件: 这是一份人教A版 (2019)8.6 空间直线、平面的垂直课堂教学ppt课件,共19页。PPT课件主要包含了导入新课,精彩课堂,图2中a∥b,课堂练习,课堂总结等内容,欢迎下载使用。
人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直背景图课件ppt: 这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直背景图课件ppt,共13页。PPT课件主要包含了复习引入,图形表示,符号表示,假设b不平行于a,反证法,符号语言,图形语言,作用证线线平行,所以棱台的体积,代入①得等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用评课课件ppt: 这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用评课课件ppt,共15页。PPT课件主要包含了符号表示,复习回顾,与AD垂直,不一定,垂足为B,∴AB⊥,关键点,①线在平面内,②线垂直于交线,提升总结等内容,欢迎下载使用。













