








2020-2021学年4.3.3 余角和补角公开课教学ppt课件
展开1.如何比较两条线段的大小?
2.借助一副三角尺画出的角,有什么规律?
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫这个角的平分线.
3.什么叫角的平分线?
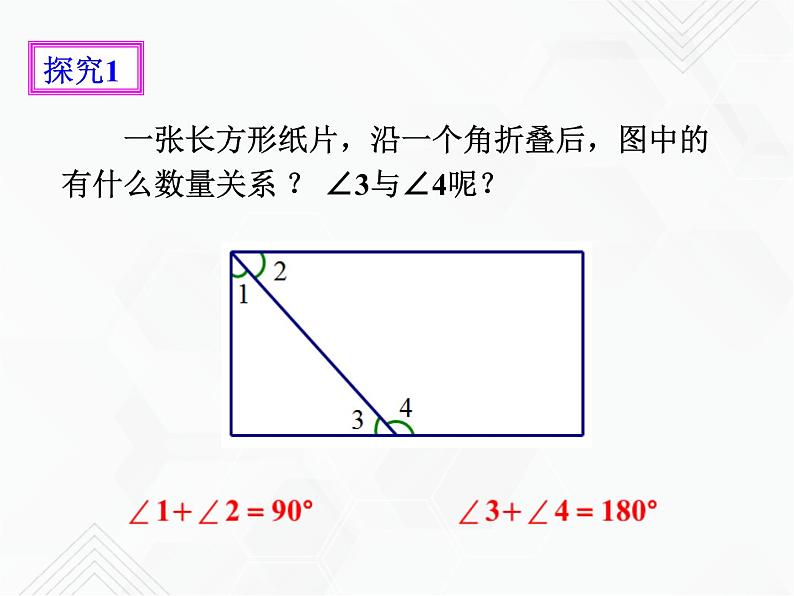
一张长方形纸片,沿一个角折叠后,图中的有什么数量关系 ? ∠3与∠4呢?
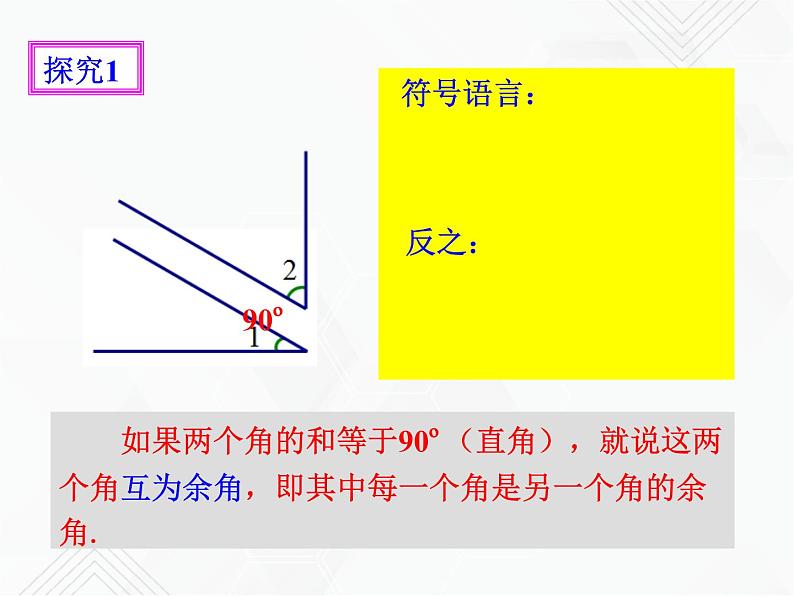
如果两个角的和等于90º(直角),就说这两个角互为余角,即其中每一个角是另一个角的余角.
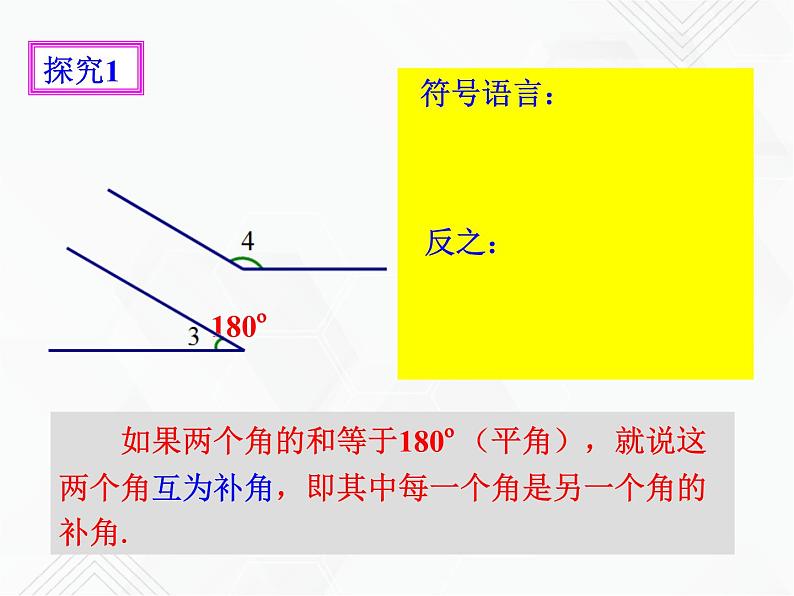
如果两个角的和等于180º(平角),就说这两个角互为补角,即其中每一个角是另一个角的补角.
1.已知∠α=35°,那么∠α的余角等于( ) A.35° B.55° C.65° D.145°2.若∠A的余角等于40°,则∠A的补角等于( ) A.40° B.50° C .130° D.140°
思考:已知∠1与∠2,∠3都互为补角.那么∠2和∠3的大小有什么关系?
由∠1与∠2和∠3都互为补角,那么 ∠2=180º-∠1, ∠3=180º-∠1,所以∠2=∠3.
你能总结出补角的一个性质?
同角(等角)的补角相等.
思考:已知∠1与∠2,∠3都互为余角.那么∠2和∠3的大小有什么关系?
由∠1与∠2和∠3都互为余角,那么 ∠2=90º-∠1, ∠3=90º-∠1,所以∠2=∠3.
余角也有类似的性质吗?
同角(等角)的余角相等.
例1.如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
解:因为A,O,B在同一直线上,所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC∠BOC,所以
所以, ∠COD 和∠COE互为余角,
同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,∠COD 和∠BOE也互为余角.
如图,直线AB与CD相交于O点,∠EOB=90°,则图中∠EOD与∠2的关系是( ) A.互补 B.互余 C.相等 D.无法确定
例2.如图,货轮O在航行过程中,发现灯塔A在它南偏东60º的方向上,同时,在它北偏东40º、南偏西10º、西北(即北偏西45º)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线.
有时以正北、正南方向为基准,描述物体运动的方向. 表示方向的角(方位角)在航行、测绘等工作中经常用到.
今天我们学习了哪些知识?
1.说一说什么是互余?什么是互补?2.余角和补角有什么性质?3.什么是方位角?
1.如果一个角的余角等于它本身,那么这个角等于_______;若一个角的补角等于它本身,则这个角等于_______.
2.若∠1+∠2=90°,∠2+∠3=90°,那么∠1=∠3,根据是_________________;如果∠1+∠2=180°,∠3+∠4=180°,且∠1=∠3,那么∠2=∠4,根据是_______________.
3.如图,下列说法正确的个数有( )①射线OA表示北偏东30°;②射线OB表示北偏西30°;③射线OD表示南偏西45°,也叫西南方向;④射线OC表示正南方向.A.1个 B.2个 C.3个 D.4个
教材140页习题4.3第12、13题.
人教版七年级上册4.3.1 角教学ppt课件: 这是一份人教版七年级上册4.3.1 角教学ppt课件,共21页。PPT课件主要包含了∠EOF,∠DOB∠AOC,同角的补角相等,图10等内容,欢迎下载使用。
初中数学人教版七年级上册4.3.3 余角和补角课前预习课件ppt: 这是一份初中数学人教版七年级上册4.3.3 余角和补角课前预习课件ppt,共22页。PPT课件主要包含了∠190°∠2,∠1+∠290°,互为补角,反馈练习,性质探索,∠1与∠2互余,∠3与∠2互余,13,同角的余角相等,等角的余角相等等内容,欢迎下载使用。
2021学年第四章 几何图形初步4.3 角4.3.1 角课文内容课件ppt: 这是一份2021学年第四章 几何图形初步4.3 角4.3.1 角课文内容课件ppt,共12页。PPT课件主要包含了图4-3-5,∠AOC-∠BOC,图4-3-6,图4-3-7等内容,欢迎下载使用。













