2021年上海市奉贤区中考数学三模试题

这是一份2021年上海市奉贤区中考数学三模试题，共24页。试卷主要包含了解答题等内容，欢迎下载使用。

2021年上海市奉贤区中考数学三模试卷
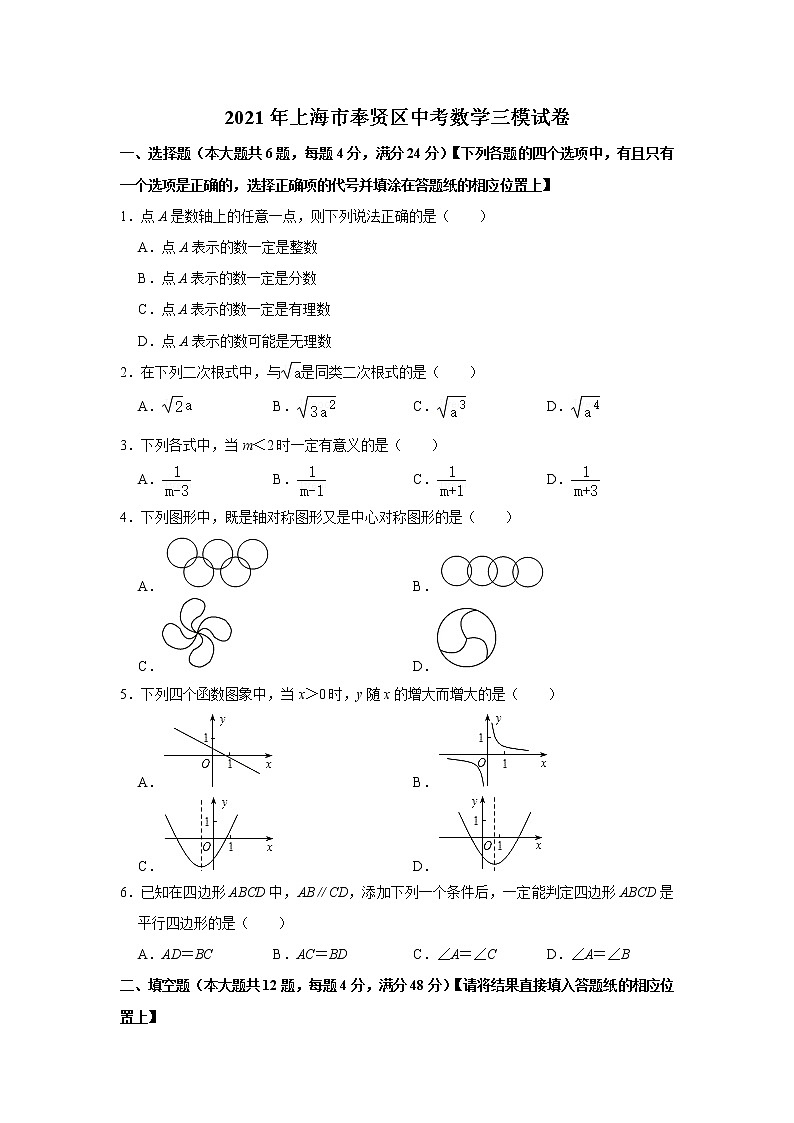
一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】
1．点A是数轴上的任意一点，则下列说法正确的是（　　）
A．点A表示的数一定是整数
B．点A表示的数一定是分数
C．点A表示的数一定是有理数
D．点A表示的数可能是无理数
2．在下列二次根式中，与是同类二次根式的是（　　）
A． B． C． D．
3．下列各式中，当m＜2时一定有意义的是（　　）
A． B． C． D．
4．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
5．下列四个函数图象中，当x＞0时，y随x的增大而增大的是（　　）
A． B．
C． D．
6．已知在四边形ABCD中，AB∥CD，添加下列一个条件后，一定能判定四边形ABCD是平行四边形的是（　　）
A．AD＝BC B．AC＝BD C．∠A＝∠C D．∠A＝∠B
二、填空题（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】
7．当x＜1时，化简：|x﹣1|＝　 　．
8．计算：（2a+b）（2a﹣b）＝　 　．
9．使得的值不大于1的x的取值范围是　 　．
10．已知函数f（x）＝，那么f（10）＝　 　．
11．已知一斜坡的坡比为1：2，坡角为α，那么sinα＝　 　．
12．已知一组数据24、27、19、13、23、12，那么这组数据的中位数是　 　．
13．将直线y＝（k+1）x﹣2平移能和直线y＝﹣3x重合，那么k的值是　 　．
14．欧阳修的《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆盖其口，徐以杓酌油沥之，自钱孔入，而钱不湿”，可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为3cm的圆面，中间有边长为1cm的正方形孔．现随机向铜钱上滴一滴油（油滴的大小忽略不计），那么油滴落入孔中的概率为　 　．
15．如图，在方格纸上建立的平面直角坐标系中，将Rt△ABC绕点C按顺时针方向旋转90°，得到Rt△FEC，则点A的对应点F的坐标是　 　．

16．如图，已知点O是正六边形ABCDEF的中心，记，，那么＝　 　（用向量、表示）．

17．我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3，如果S1+S2+S3＝48，那么S2的值是　 　.
18．如图，已知在等边△ABC中，AB＝4，点P在边BC上，如果以线段PB为半径的⊙P与以边AC为直径的⊙O外切，那么⊙P的半径长是　 　．

三、解答题（共7小题，满分78分）
19．（10分）计算：（π﹣3）0﹣||+（）+．
20．（10分）解方程：＝﹣1．
21．（10分）如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：
①以点O为原点、网格边长为单位长，建立平面直角坐标系；
②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：C　 　、D　 　；
②⊙D的半径＝　 　；
（3）求∠ACO的正弦值．

22．（10分）阅读下列有关记忆的资料，分析保持记忆的措施和方法．资料：德国心理学家艾宾浩斯对人的记忆进行了研究，他采用无意义的音节作为记忆的材料进行实验，获得了如表中的相关数据，然后他又根据表中的数据绘制了一条曲线，这就是著名的艾宾浩斯遗忘曲线．其中横轴表示时间，纵轴表示学习中的记忆量．
时间
记忆量
刚记忆完
100%
20分钟后
58.2%
1个小时后
44.2%
9个小时后
35.8%
1天后
33.7%
2天后
27.8%
6天后
25.4%
30天后
21.1%
观察表格和图象，回答下列问题：
（1）图中点A的坐标表示的实际意义是　 　；
（2）在下面哪个时间段内遗忘的速度最快　 　．
A.0﹣20分钟
B.20分钟﹣1小时
C.1小时﹣9小时
D.1天﹣2天
（3）王老师每节数学课最后五分钟都会对本节课进行回顾总结，并要求学生每天晚上对当天课堂上所学的知识进行复习．据调查这样一天后记忆量能保持98%，如果小明同学一天没有复习，那么记忆量大约会比复习过的记忆量减少多少？由此对你的学习有什么启示？

23．（12分）已知：如图，在△ABC中，AD⊥BC，垂足为点D，AD＝BD，点E为边AD上一点，且DE＝DC，联结BE并延长，交边AC于点F．
（1）求证：BF⊥AC；
（2）过点A作BC的平行线交BF的延长线于点G，联结CG．如果DE2＝AE•AD，求证：四边形ADCG是矩形．

24．（12分）如图，已知在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2）．
（1）求这条抛物线的表达式；
（2）如果将抛物线向下平移m个单位，使平移后的抛物线的顶点恰好落在线段BC上，求m的值；
（3）如果点P是抛物线位于第一象限上的点，联结PA，交线段BC于点E，当PE：AE＝4：5时，求点P的坐标．

25．（14分）已知在△ABC中，∠C＝90°，BC＝8，cosB＝，点D是边BC上一点，过点D作DE⊥AB，垂足为点E，点F是边AC上一点，联结DF、EF，以DF、EF为邻边作平行四边形EFDG．
（1）如图1，如果CD＝2，点G恰好在边BC上，求∠CDF的余切值；
（2）如图2，如果AF＝AE，点G在△ABC内，求线段CD的取值范围；
（3）在第（2）小题的条件下，如果平行四边形EFDG是矩形，求线段CD的长.

2021年上海市奉贤区中考数学三模试卷
参考答案与试题解析
一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】
1．点A是数轴上的任意一点，则下列说法正确的是（　　）
A．点A表示的数一定是整数
B．点A表示的数一定是分数
C．点A表示的数一定是有理数
D．点A表示的数可能是无理数
【分析】根据数轴上的点与实数一一对应，可得答案．
【解答】解：数轴上的点与实数一一对性应，故A错误；
数轴上的点与实数一一对应，故B错误；
根据互为相反数的两个数的绝对值相等，故C错误；
数轴上的点与实数一一对应，所以点A有可能是无理数，故D正确；
故选：D．
2．在下列二次根式中，与是同类二次根式的是（　　）
A． B． C． D．
【分析】先将各选项化简，再找到被开方数为a的选项即可．
【解答】解：A、a与被开方数不同，故不是同类二次根式；
B、＝|a|与被开方数不同，故不是同类二次根式；
C、＝|a|与被开方数相同，故是同类二次根式；
D、＝a2与被开方数不同，故不是同类二次根式．
故选：C．
3．下列各式中，当m＜2时一定有意义的是（　　）
A． B． C． D．
【分析】根据分式意义的条件是分母不等于0判断即可．
【解答】解：A．当m＜2时，m﹣3＜﹣1，故分式一定有意义，故本选项符合题意；
B．m＜2，当m＝1时，分式没有意义，故本选项不符合题意；
C．m＜2，当m＝﹣1时，分式没有意义，故本选项不符合题意；
D..m＜2，当m＝﹣3时，分式没有意义，故本选项不符合题意；
故选：A．
4．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A． B．
C． D．
【分析】根据轴对称图形与中心对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．
如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
【解答】解：A、是轴对称图形，不是中心对称图形，故此选项错误；
B、是轴对称图形也是中心对称图形，故此选项正确；
C、不是轴对称图形，是中心对称图形．故此选项错误；
D、不是轴对称图形，也不是中心对称图形，故此选项错误．
故选：B．
5．下列四个函数图象中，当x＞0时，y随x的增大而增大的是（　　）
A． B．
C． D．
【分析】分别根据各函数图象的特点进行逐一分析即可．
【解答】解：A、错误，此函数为减函数，y随x的增大而减小；
B、错误，此函数为反比例函数，x＞0时，y随x的增大而减小；
C、正确，此函数为二次函数，x＞0时，y随x的增大而增大；
D、错误，此函数为二次函数，x＞0时，在对称轴的左侧y随x的增大而减小，在对称轴的右侧y随x的增大而增大．
故选：C．
6．已知在四边形ABCD中，AB∥CD，添加下列一个条件后，一定能判定四边形ABCD是平行四边形的是（　　）
A．AD＝BC B．AC＝BD C．∠A＝∠C D．∠A＝∠B
【分析】利用平行线的判定与性质结合平行四边形的判定得出即可．
【解答】解：如图所示：∵AB∥CD，
∴∠B+∠C＝180°，
当∠A＝∠C时，则∠A+∠B＝180°，
故AD∥BC，
则四边形ABCD是平行四边形．
故选：C．

二、填空题（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】
7．当x＜1时，化简：|x﹣1|＝　1﹣x　．
【分析】正数的绝对值等于它本身，负数的绝对值等于它的相反数，0的绝对值是0．
【解答】解：∵x＜1，
∴x﹣1＜0，
∴原式＝﹣（x﹣1）
＝1﹣x．
8．计算：（2a+b）（2a﹣b）＝　4a2﹣b2　．
【分析】根据平方差公式，即可解答．
【解答】解：（2a+b）（2a﹣b）＝4a2﹣b2，
故答案为：4a2﹣b2．
9．使得的值不大于1的x的取值范围是　x≤6　．
【分析】由题意可知：x﹣1的值不大于1，即x﹣1≤1，则列出不等式即可解得x的取值．
【解答】解：∵代数式x﹣1的值不大于1，
即x﹣1≤1，
移项得x≤2，
两边同乘3可得x≤6，
所以，x的取值范围为x≤6．
故答案为：x≤6．
10．已知函数f（x）＝，那么f（10）＝　2　．
【分析】根据已知直接将x＝10代入求出答案．
【解答】解：∵f（x）＝，
∴f（10）＝＝2．
故答案为：2．
11．已知一斜坡的坡比为1：2，坡角为α，那么sinα＝　　．
【分析】坡比＝坡角的正切值，设竖直直角边为x，水平直角边为2x，由勾股定理求出斜边，进而可求出α的正弦值．
【解答】解：如图所示：
由题意，得：tanα＝i＝，
设竖直直角边为x，水平直角边为2x，
则斜边＝＝x，
则sinα＝＝．
故答案为．

12．已知一组数据24、27、19、13、23、12，那么这组数据的中位数是　21　．
【分析】求中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．
【解答】解：将这组数据从小到大的顺序排列：12、13、19、23、24、27，处于中间位置的两个数是19，23，那么由中位数的定义可知，这组数据的中位数是（19+23）÷2＝21．
故答案为：21．
13．将直线y＝（k+1）x﹣2平移能和直线y＝﹣3x重合，那么k的值是　﹣4　．
【分析】根据直线y＝（k+1）x﹣2平移能和直线y＝﹣3x重合，可得k+1＝﹣3，即可得k的值．
【解答】解：∵将直线y＝（k+1）x﹣2平移能和直线y＝﹣3x重合，
∴直线y＝（k+1）x﹣2和直线y＝﹣3x平行，
∴k+1＝﹣3，
解得k＝﹣4，
故答案为：﹣4．
14．欧阳修的《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆盖其口，徐以杓酌油沥之，自钱孔入，而钱不湿”，可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为3cm的圆面，中间有边长为1cm的正方形孔．现随机向铜钱上滴一滴油（油滴的大小忽略不计），那么油滴落入孔中的概率为　　．
【分析】分别计算圆和正方形的面积，由几何概型概率公式可得答案．
【解答】解：∵S正方形＝1，S圆＝（）2×π＝，
∴P＝＝．
故答案为：．
15．如图，在方格纸上建立的平面直角坐标系中，将Rt△ABC绕点C按顺时针方向旋转90°，得到Rt△FEC，则点A的对应点F的坐标是　（﹣1，2）　．

【分析】根据网格图形找出点A、B顺时针旋转90°后的对应点的位置，然后顺次连接，再根据平面直角坐标系写出点F的坐标即可．
【解答】解：如图，点F的坐标为（﹣1，2）．
故答案为：（﹣1，2）．

16．如图，已知点O是正六边形ABCDEF的中心，记，，那么＝　　（用向量、表示）．

【分析】由正六边形的性质可得＝，求出，再由是的相反向量，可得出答案．
【解答】解：连接OE，
∵六边形ABCDEF是正六边形，
∴FE＝OD，
∴＝，
∴＝+＝+，
∴＝﹣＝﹣﹣．
故答案为：﹣﹣．
17．我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1）．图2由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3，如果S1+S2+S3＝48，那么S2的值是　16　.
【分析】根据正方形的面积和勾股定理即可求解．
【解答】解：设全等的直角三角形的两条直角边为a、b且a＞b，
由题意可知：S1＝（a+b）2，S2＝a2+b2，S3＝（a﹣b）2，
因为S1+S2+S3＝48，
即（a+b）2+a2+b2+（a﹣b）2＝21，
∴3（a2+b2）＝48，
∴3S2＝48，
∴S2的值是16．
故答案为16．
18．如图，已知在等边△ABC中，AB＝4，点P在边BC上，如果以线段PB为半径的⊙P与以边AC为直径的⊙O外切，那么⊙P的半径长是　　．

【分析】由等边三角形的性质和直角三角形的性质可求CH，OH，由勾股定理可求解．
【解答】解：如图，连接OP，过点O作OH⊥BC于P，

在等边△ABC中，AB＝4，
∴AC＝BC＝AB＝4，∠ACB＝60°，
∵点O是AC的中点，
∴AO＝OC＝2，
∵以线段PB为半径的⊙P与以边AC为直径的⊙O外切，
∴PO＝2+BP，
∵OH⊥BC，
∴∠COH＝30°，
∴HC＝1，OH＝，
∵OP2＝OH2+PH2，
∴（2+BP）2＝3+（4﹣1﹣BP）2，
∴BP＝，
故答案为．
三、解答题（共7小题，满分78分）
19．（10分）计算：（π﹣3）0﹣||+（）+．
【分析】原式第一项利用零指数公式化简，第二项利用负数的绝对值等于它的相反数化简，第三项利用负指数公式化简最后一项分母有理化，去括号合并同类二次公式，即可得到结果．
【解答】解：原式＝1﹣（2﹣）++＝1﹣2+++2（2﹣）＝1﹣2+++4﹣2＝3．
20．（10分）解方程：＝﹣1．
【分析】观察可得最简公分母是（x+2）（x﹣2），方程两边乘最简公分母，可以把分式方程转化为整式方程求解．
【解答】解：去分母，得4＝（x+2）﹣（x+2）（x﹣2），
整理，得x2﹣x﹣2＝0，
解得x1＝﹣1，x2＝2．
经检验：x1＝﹣1是原方程的根，x2＝2是增根．
故原方程的根为x＝﹣1．
21．（10分）如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．
（1）请完成如下操作：
①以点O为原点、网格边长为单位长，建立平面直角坐标系；
②根据图形提供的信息，标出该圆弧所在圆的圆心D，并连接AD、CD．
（2）请在（1）的基础上，完成下列填空：
①写出点的坐标：C　（6，2）　、D　D（2，0）　；
②⊙D的半径＝　2　；
（3）求∠ACO的正弦值．

【分析】（1）根据点的坐标的表示，C的坐标即可得到，首先作出弦AB与BC的中垂线，中垂线的交点就是D，即可确定点D的坐标；
（2）①根据（1）中的平面直角坐标系直接填空；
②在直角△AOD中，利用勾股定理即可求解；
（3）连接AC、OC．过C作CH⊥AO于点H，过点A作AM⊥CO于点M．利用三角形AOC的面积等积转换求得AM的长度，然后在
Rt△AMC中利用正弦函数的定义求得∠ACO的正弦值．
【解答】解：（1）直角坐标系、点D的在该坐标系中的位置如图所示：

（2）解：①根据图示知，C（6，2），D（2，0），
故答案为：（6，2），（2，0）；

②解：在直角△AOD中，根据勾股定理知⊙D的半径AD＝＝＝2，
故答案为：2；

（3）解：连接AC、OC．过C作CH⊥AO于点H，过点A作AM⊥CO于点M．
则OA•CH＝OC•AM，即×4×6＝×2•AM，
解得，AM＝；
在Rt△AMC中，sin∠ACO＝＝＝．

22．（10分）阅读下列有关记忆的资料，分析保持记忆的措施和方法．资料：德国心理学家艾宾浩斯对人的记忆进行了研究，他采用无意义的音节作为记忆的材料进行实验，获得了如表中的相关数据，然后他又根据表中的数据绘制了一条曲线，这就是著名的艾宾浩斯遗忘曲线．其中横轴表示时间，纵轴表示学习中的记忆量．
时间
记忆量
刚记忆完
100%
20分钟后
58.2%
1个小时后
44.2%
9个小时后
35.8%
1天后
33.7%
2天后
27.8%
6天后
25.4%
30天后
21.1%
观察表格和图象，回答下列问题：
（1）图中点A的坐标表示的实际意义是　27.8%　；
（2）在下面哪个时间段内遗忘的速度最快　A　．
A.0﹣20分钟
B.20分钟﹣1小时
C.1小时﹣9小时
D.1天﹣2天
（3）王老师每节数学课最后五分钟都会对本节课进行回顾总结，并要求学生每天晚上对当天课堂上所学的知识进行复习．据调查这样一天后记忆量能保持98%，如果小明同学一天没有复习，那么记忆量大约会比复习过的记忆量减少多少？由此对你的学习有什么启示？

【分析】（1）依据图象中点的坐标，即可得到A点表示的意义；
（2）根据图象判断即可；
（3）依据函数图象，可得如果一天不复习，记忆量只能保持33.7%左右，据此列式计算即可．
【解答】解：（1）由题可得，点A表示：2天大约记忆量保持了27.8%；
故答案为：27.8%；
（2）由图可得，0﹣20分钟 内记忆保持量下降41.8%，故0﹣20分钟内内遗忘的速度最快，
故选：A；
（3）如果一天不复习，记忆量只能保持33.7%，记忆量减少约98%﹣33.7%＝64.3%；
学习计划两条：①每天上午、下午、晚上各复习10分钟；②坚持每天复习，劳逸结合（答案不唯一）．
23．（12分）已知：如图，在△ABC中，AD⊥BC，垂足为点D，AD＝BD，点E为边AD上一点，且DE＝DC，联结BE并延长，交边AC于点F．
（1）求证：BF⊥AC；
（2）过点A作BC的平行线交BF的延长线于点G，联结CG．如果DE2＝AE•AD，求证：四边形ADCG是矩形．

【分析】（1）先证明△BDE和△ADC全等得出∠EBD＝∠CAD，再证△BDE≌△ADC，即可得证；
（2）先证四边形ADCG是平行四边形，再证一个角是直角即可得证．
【解答】（1）证明：∵AD⊥BC，
∠ADC＝∠BDE＝90°，
在△ACD和△BED中，
，
∴△ACD≌△BED（SAS），
∴∠EBD＝∠CAD，
又∵∠BED＝∠AEF，
∴△BED∽△AEF，
∴∠AFE＝∠EDB＝90°，
即BF⊥AC；
（2）证明：∵AG∥BC，
∴∠AGE＝∠EDB，
由（1）知∠EBD＝∠CAD，
∴∠AGE＝∠CAD，
又∵∠AEG＝∠BED＝∠ACD，
∴△AEG∽△DCA，
∴＝，
∴AE•AD＝DC•AG，
∵DE2＝AE•AD，DE＝DC，
∴DC•AG＝DE2＝DC2，
∴DC＝AG，
又∵AG∥DC，
∴四边形ADCG是平行四边形，
∵AD⊥BC，
∴四边形ADCG是矩形（有一个角是直角的平行四边形是矩形）．

24．（12分）如图，已知在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2）．
（1）求这条抛物线的表达式；
（2）如果将抛物线向下平移m个单位，使平移后的抛物线的顶点恰好落在线段BC上，求m的值；
（3）如果点P是抛物线位于第一象限上的点，联结PA，交线段BC于点E，当PE：AE＝4：5时，求点P的坐标．

【分析】（1）利用待定系数法可求解析式；
（2）求出平移前后的顶点坐标，即可求解；
（3）通过证明△AEF∽△APH，可证＝，即可求解．
【解答】解：（1）∵y＝﹣x2+bx+c与x轴交于点A（﹣1，0），与y轴交于点C（0，2）．
∴，
解得：，
∴抛物线解析式为y＝﹣x2+x+2；
（2）∵y＝﹣x2+x+2＝﹣（x﹣）2+，
∴顶点坐标为（，），
∵y＝﹣x2+x+2与x轴交于点A，点B，
∴0＝﹣x2+x+2，
∴x1＝﹣1，x2＝4，
∴点B（4，0），
设直线BC解析式为y＝kx+n，
，
解得：，
∴直线BC解析式为y＝﹣x+2，
当x＝时，y＝，
∴m＝＝；
（3）如图，过点E作EF⊥AB于F，过点P作PH⊥AB于H，

∴EF∥PH，
∴△AEF∽△APH，
∴，
∵PE：AE＝4：5，
∴＝，
∴AF＝5x，AH＝9x，
∴OF＝5x﹣1，OH＝9x﹣1，
∴点E坐标为[5x﹣1，﹣（5x﹣1）+2]，点P坐标为[9x﹣1，﹣（9x﹣1）2+（9x﹣1）+2]，
∴EF＝﹣（5x﹣1）+2，PH＝﹣（9x﹣1）2+（9x﹣1）+2，
∴＝，
∴x＝，
∴点P（2，3）．
25．（14分）已知在△ABC中，∠C＝90°，BC＝8，cosB＝，点D是边BC上一点，过点D作DE⊥AB，垂足为点E，点F是边AC上一点，联结DF、EF，以DF、EF为邻边作平行四边形EFDG．
（1）如图1，如果CD＝2，点G恰好在边BC上，求∠CDF的余切值；
（2）如图2，如果AF＝AE，点G在△ABC内，求线段CD的取值范围；
（3）在第（2）小题的条件下，如果平行四边形EFDG是矩形，求线段CD的长.
【分析】（1）由锐角三角函数的定义求出BC＝8，由勾股定理求出AC＝6，由平行线分线段成比例定理得出，求出CF，则可得出答案；
（2）当点G恰好在AB上时，解直角三角形求出CD的长，则可得出答案；
（3）设CD＝x，则BE＝（8﹣x），设矩形EFDG的对角线FG与DE相交于点O，连接OA，证明△AFO≌△AEO（SSS），由全等三角形的性质得出∠AFO＝∠AEO＝90°，过点E作EH⊥AC于点H，由梯形的中位线定理得出EH+CD＝2OF＝DE，解方程[10﹣（8﹣x）]+x＝（8﹣x）可得出答案．
【解答】解：（1）在Rt△ABC中，cosB＝＝，
又BC＝8，
∴AB＝10，
∴AC＝＝＝6，
∵DE⊥AB，
∴在Rt△BDE中，
cosB＝，
又CD＝2，BD＝6，
∴BE＝，
∵四边形ABCD是平行四边形，
∴EF∥DG，
∵点G在BC上，
∴EF∥BC，
∴，
∴，
∴CF＝，
在Rt△CFD中，cos＝；
（2）∵四边形EFDG是平行四边形，
∴DF∥EG，
当点G恰好在AB上时，
∴DF∥AB，
∴，
设CD＝x，则，
∴CF＝，
在Rt△BDE中，cosB＝，
又CD＝x，则BD＝8﹣x，
∴BE＝（8﹣x），
∵AE＝AF，
∴，
∴x＝，
当点G在△ABC内时，0≤CD；
（3）设CD＝x，则BE＝（8﹣x），
∴AE＝10﹣（8﹣x），
设矩形EFDG的对角线FG与DE相交于点O，连接OA，

∵平行四边形EFDG是矩形，
∴OF＝OE＝DE，
∵AF＝AE，OA＝OA，
∴△AFO≌△AEO（SSS），
∴∠AFO＝∠AEO＝90°，
过点E作EH⊥AC于点H，
又∠C＝90°，
∴EH∥HF∥CB，
∵OD＝OE，
∴CF＝HF，
∴EH+CD＝2OF＝DE，
∵（8﹣x），EH＝[10﹣（8﹣x）]，
∴[10﹣（8﹣x）]+x＝（8﹣x），
∴x＝，
∴CD＝．