初中数学鲁教版 (五四制)九年级上册第三章 二次函数综合与测试习题ppt课件

这是一份初中数学鲁教版 (五四制)九年级上册第三章 二次函数综合与测试习题ppt课件，共27页。PPT课件主要包含了答案呈现等内容，欢迎下载使用。
【点拨】如图，建立如图所示的平面直角坐标系，由题意可得MN＝4米，EF＝14米，BC＝10米，DO＝1.5米．
【2019·襄阳】如图，若被击打的小球飞行高度h(m)与飞行时间t(s)之间具有的关系为h＝20t－5t2，则小球从飞出到落地所用的时间为________s.
【2019·临沂】从地面竖直向上抛出一小球，小球的高度h(m)与小球运动时间t(s)之间的函数关系如图所示．给出下列结论：①小球在空中经过的路程是40 m；②小球抛出3 s后，速度越来越快；③小球抛出3 s时速度为0；④小球的高度h＝30 m时，t＝1.5 s.其中正确的是(　　)A．①④ B．①② C．②③④ D．②③
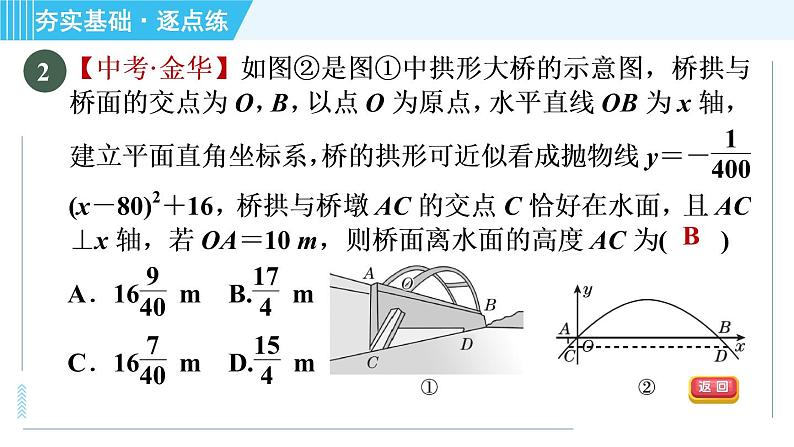
【中考·北京】跳台滑雪是冬季奥运会比赛项目之一，运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度y(m)与水平距离x(m)近似满足函数关系y＝ax2＋bx＋c(a≠0)，如图记录了某运动员起跳后的x与y的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为(　　)A．10 m B．15 m C．20 m D．22.5 m
(1)求该抛物线对应的函数表达式，并计算出 拱顶D到地面OA的距离．
(2)一辆货运汽车载一长方体集装箱后高为6 m，宽为4 m，如果隧道内设双向行车道，那么这辆货运汽车能否安全通过？
(3)在抛物线形拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8 m，那么两排灯的水平距离最小是多少米？
【2020·台州】用各种盛水容器可以制作精致的家用流水景观(如图①)．科学原理：如图②，始终盛满水的圆柱体水桶水面离地面的高度为H(单位：cm)，如果在离水面竖直距离为h(单位：cm)的地方开大小合适的小孔，那么从小孔射出水的射程(水流落地点离小孔的水平距离)s(单位：cm)与h的关系为s2＝4h(H－h)．
应用思考：现用高度为20 cm的圆柱体塑料水瓶做相关研究，水瓶直立地面，通过连续注水保证它始终盛满水，在离水面竖直距离为h cm处开一个小孔．(1)写出s2与h的关系式，并求出当h为何值时，射程s有最大值，最大射程是多少？
解：∵s2＝4h(H－h)，∴当H＝20时，s2＝4h(20－h)＝－4(h－10)2＋400.∴当h＝10时，s2有最大值400，∴当h＝10时，s有最大值20.即当h为10时，射程s有最大值，最大射程是20 cm.
(2)在侧面开两个小孔，这两个小孔离水面的竖直距离分别为a，b，要使两孔射出水的射程相同，求a，b之间的关系式．
解：要使两孔射出水的射程相同，则有：4a(20－a)＝4b(20－b)，∴20a－a2＝20b－b2，∴a2－b2＝20a－20b，∴(a＋b)(a－b)＝20(a－b)，∴(a－b)(a＋b－20)＝0，∴a－b＝0或a＋b－20＝0，∴a＝b或a＋b＝20.
(3)如果想通过垫高塑料水瓶，使射出水的最大射程增加16 cm，求垫高的高度及小孔离水面的竖直距离．
【2020·嘉兴】在篮球比赛中，东东投出的球在点A处反弹，反弹后球运动的路线为抛物线的一部分(如图①所示建立直角坐标系)，抛物线顶点为点B.(1)求该抛物线的函数表达式．
解：设y＝a(x－0.4)2＋3.32(a≠0)，把x＝0，y＝3代入，解得a＝－2，∴抛物线的函数表达式为y＝－2(x－0.4)2＋3.32.
(2)当球运动到点C时被东东抢到，CD⊥x轴于点D，CD＝2.6 m.①求OD的长．
解：把y＝2.6代入y＝－2(x－0.4)2＋3.32，化简得(x－0.4)2＝0.36，解得x1＝－0.2(舍去)，x2＝1，∴OD＝1 m.
②东东抢到球后，因遭对方防守无法投篮，他在点D处垂直起跳传球，想将球沿直线快速传给队友华华，目标为华华的接球点E(4，1.3)．东东起跳后所持球离地面高度h1(m)(传球前)与东东起跳后时间t(s)满足函数关系式h1＝－2(t－0.5)2＋2.7(0≤t≤1)；小戴在点F(1.5，0)处拦截，他比东东晚0.3 s垂直起跳，其拦截高度h2(m)与东东起跳后时间t(s)的函数关系如图②所示(其中两条抛物线的形状相同)．东东的直线传球能否越过小戴的拦截传到点E？若能，东东应在起跳后什么时间范围内传球？若不能，请说明理由(直线传球过程中球运动时间忽略不计)．
解：东东的直线传球能越过小戴的拦截传到点E.如图，由图①可得，当0≤t≤0.3时，h2＝2.2.当0.3＜t≤1.3时，易得h2＝－2(t－0.8)2＋2.7.当h1－h2＝0时，t＝0.65，东东在点D起跳传球与小戴在点F处拦截的示意图如图②，设MD＝h1，NF＝h2，当点M，N，E三点共线时，过点E作EG⊥MD于点G，交NF于点H，过点N作NP⊥MD于点P.