






















































































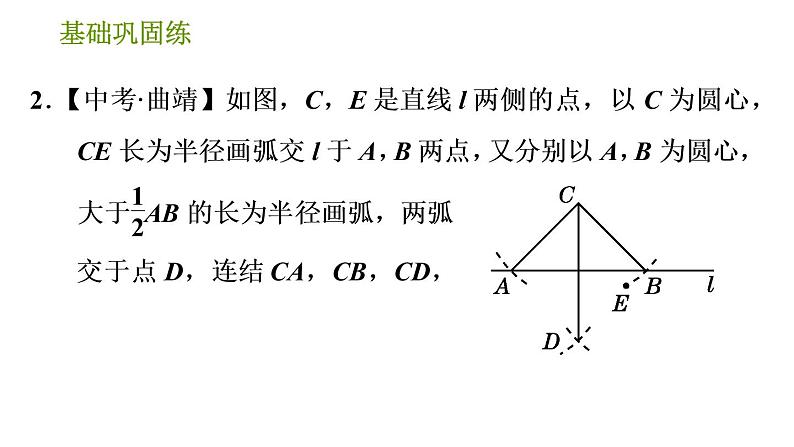

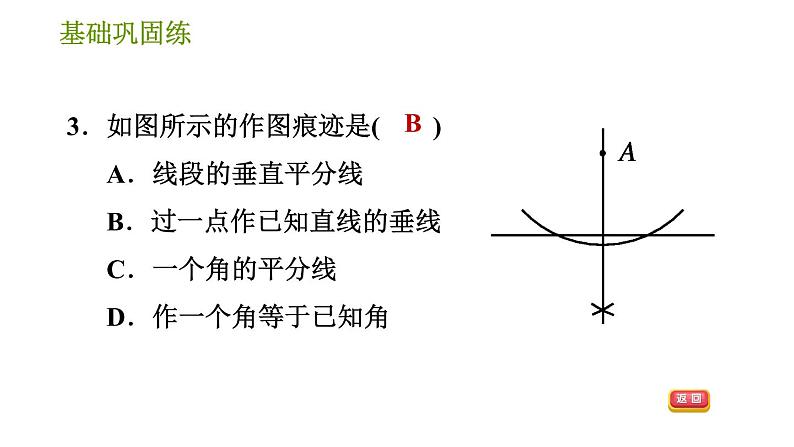
























初中第13章 全等三角形综合与测试习题课件ppt
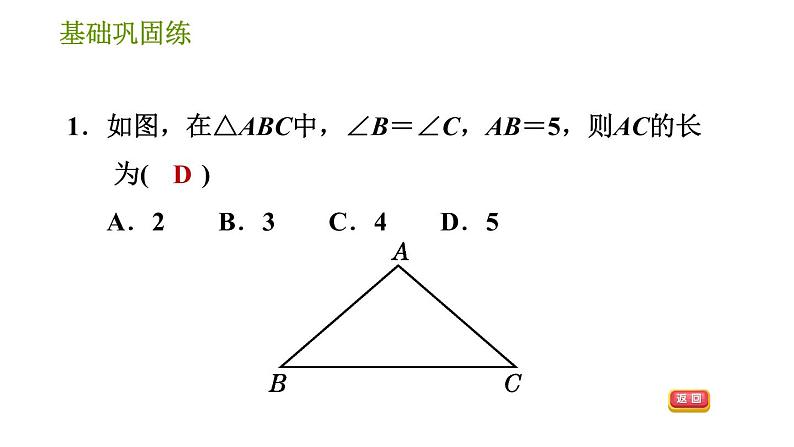
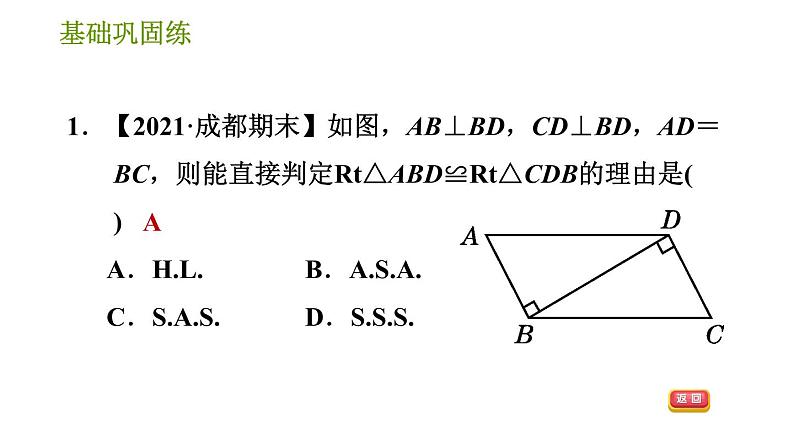
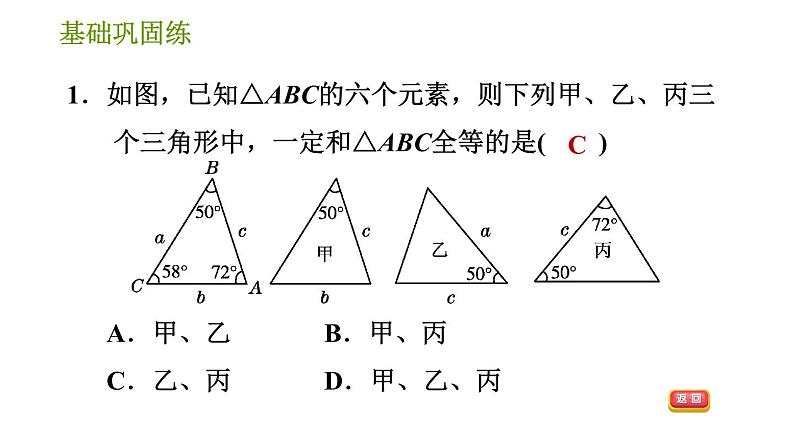
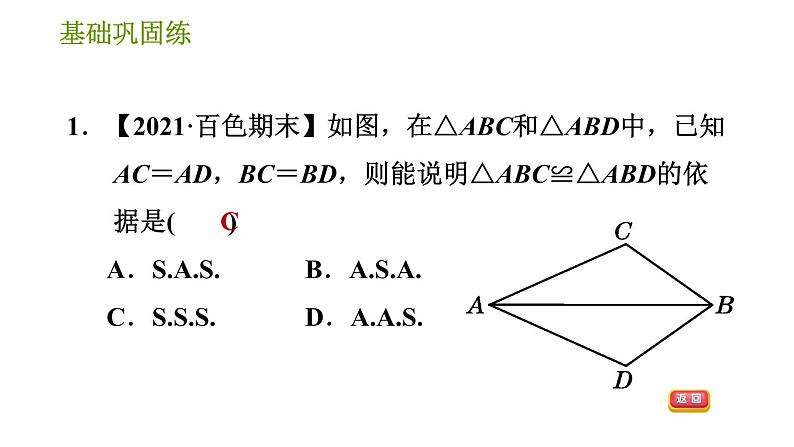
展开两边及其________分别相等的两个三角形全等.简记为 (或边角边).其书写模式为:
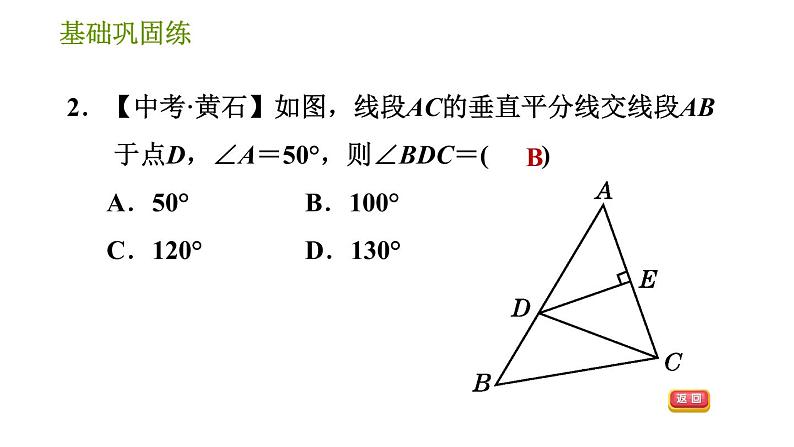
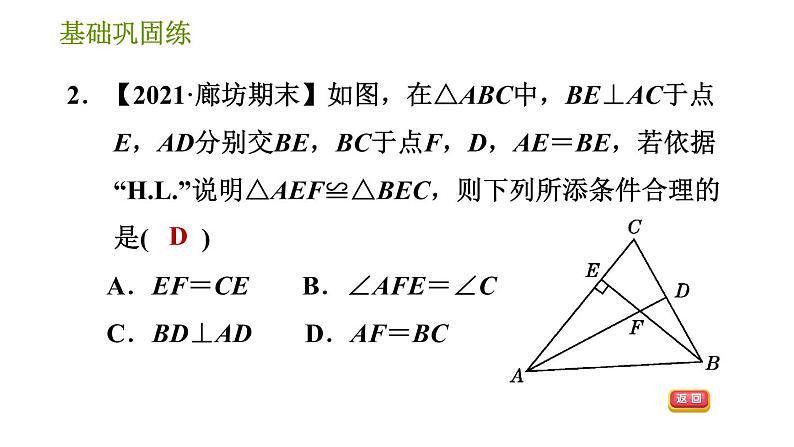
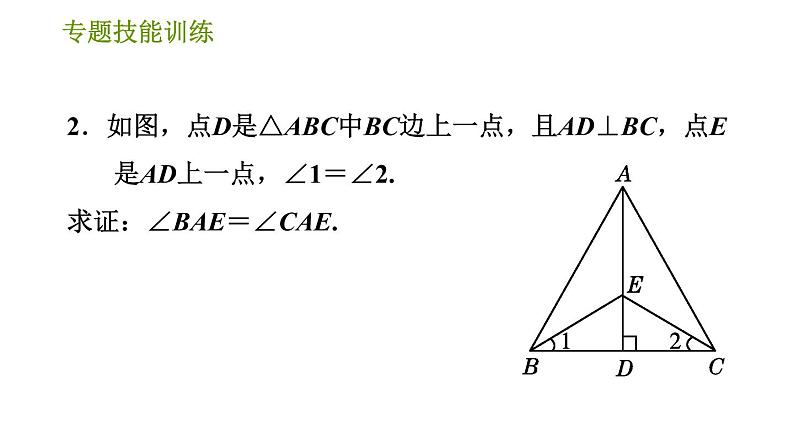
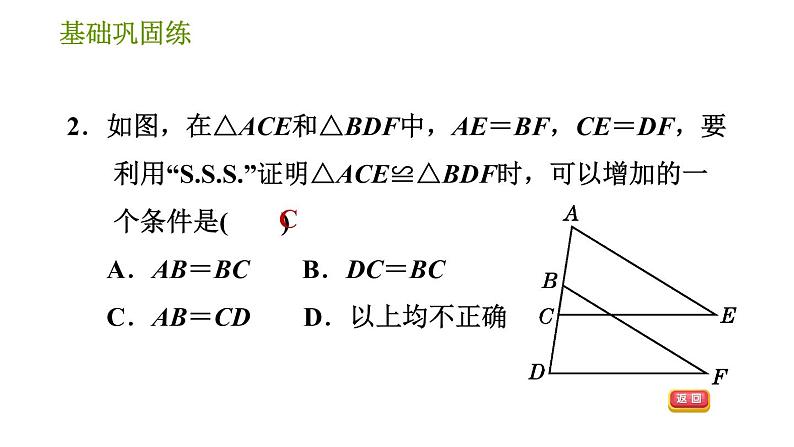
∴△ABC≌△A′B′C′.
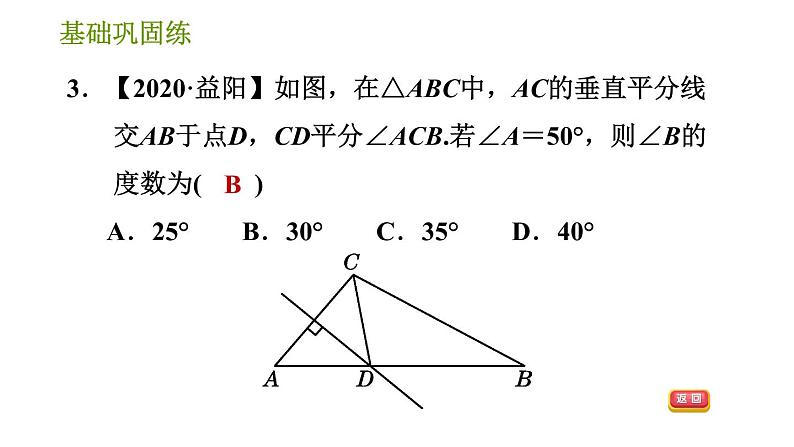
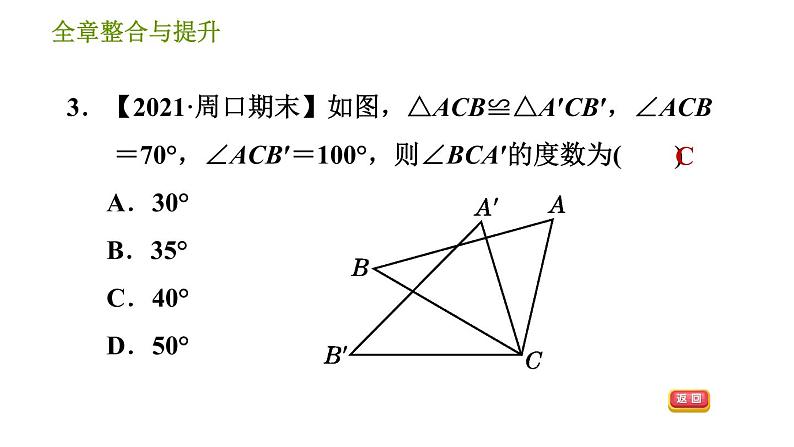
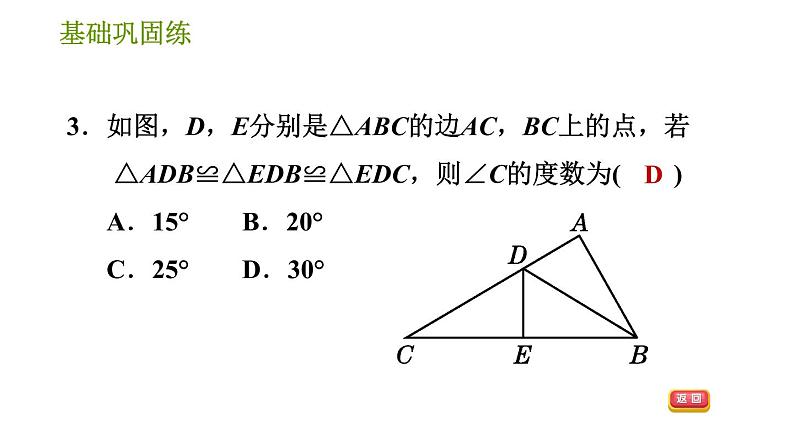
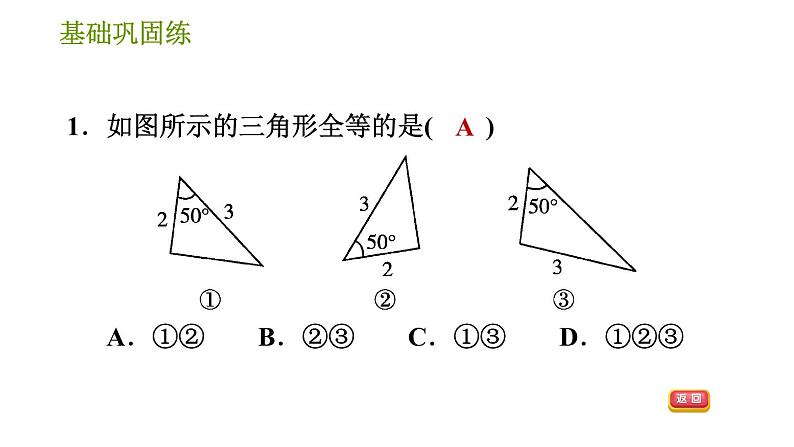
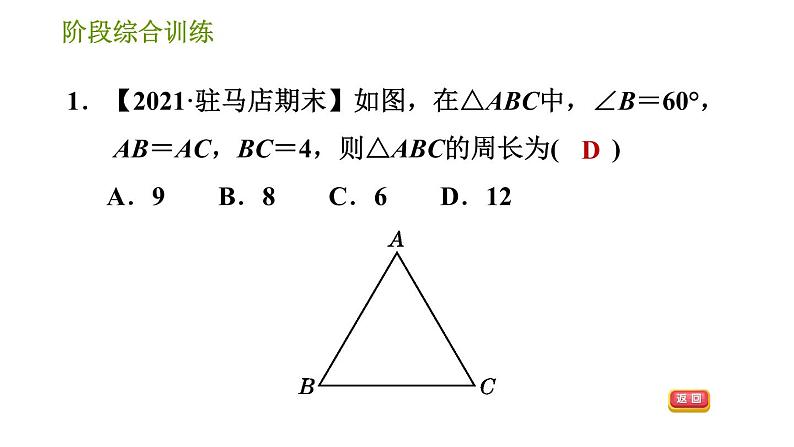
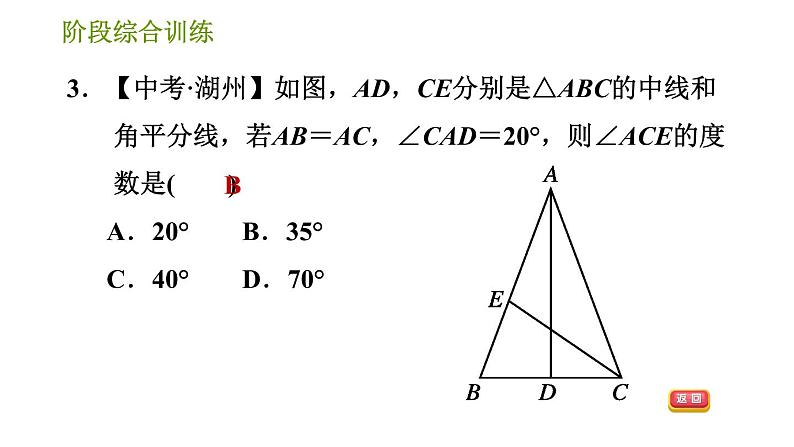
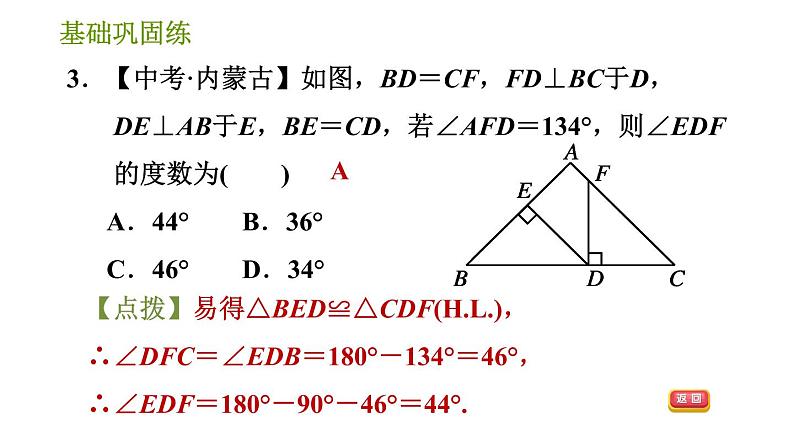
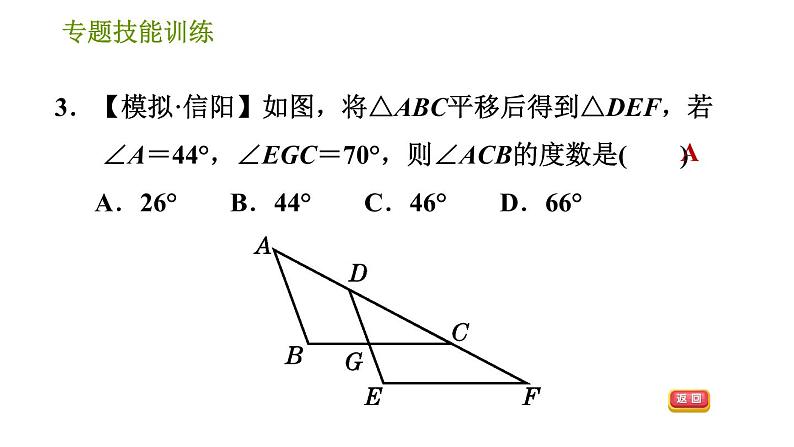
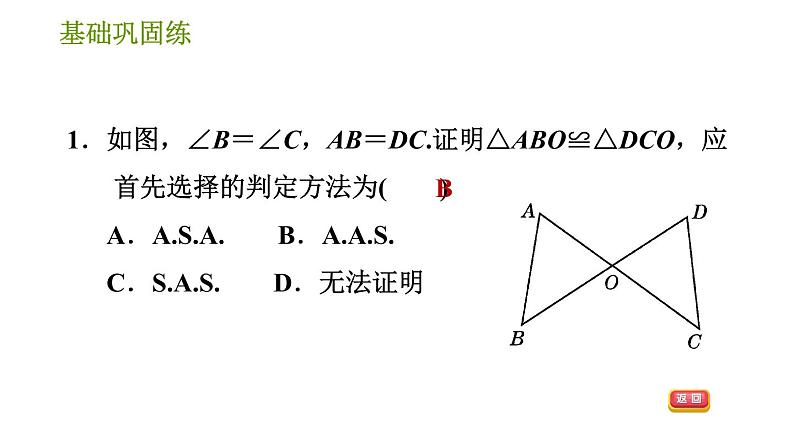
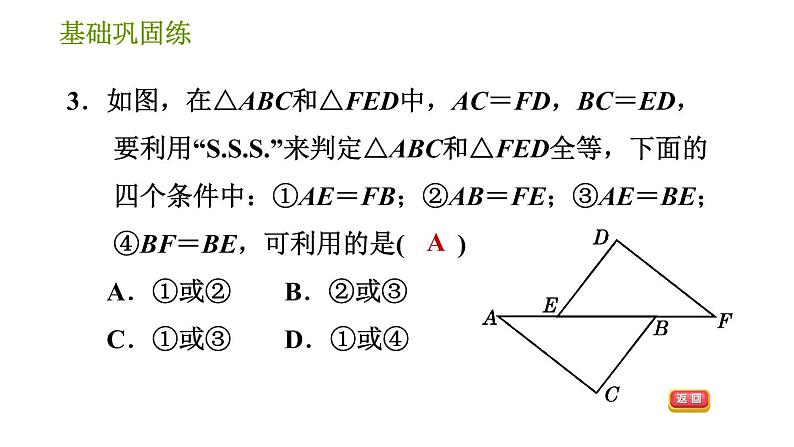
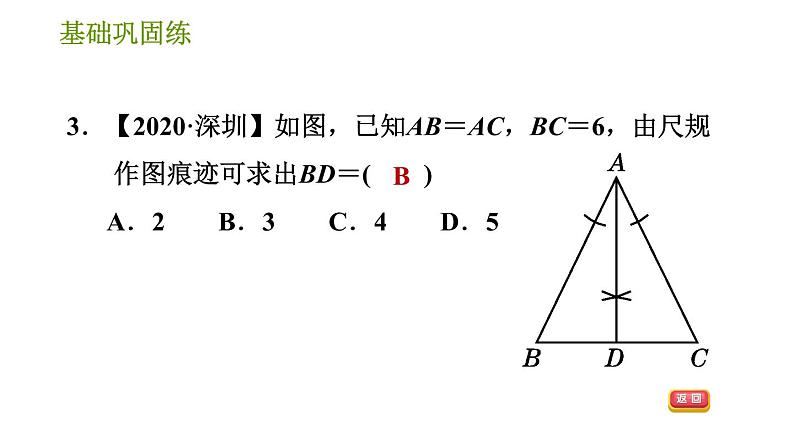
1.如图所示的三角形全等的是( ) A.①② B.②③ C.①③ D.①②③
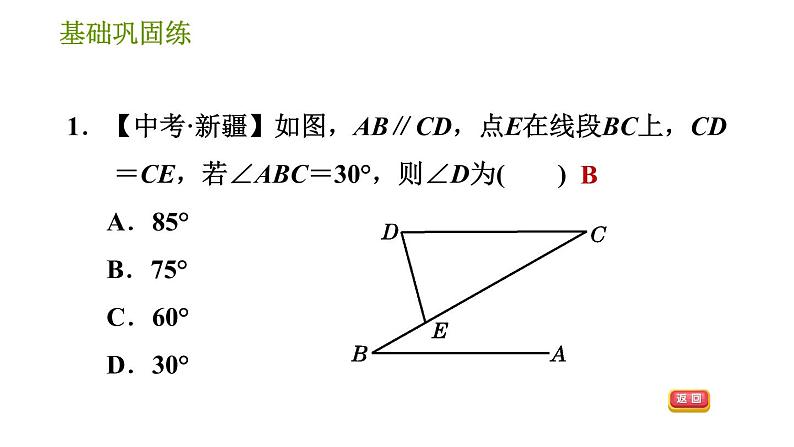
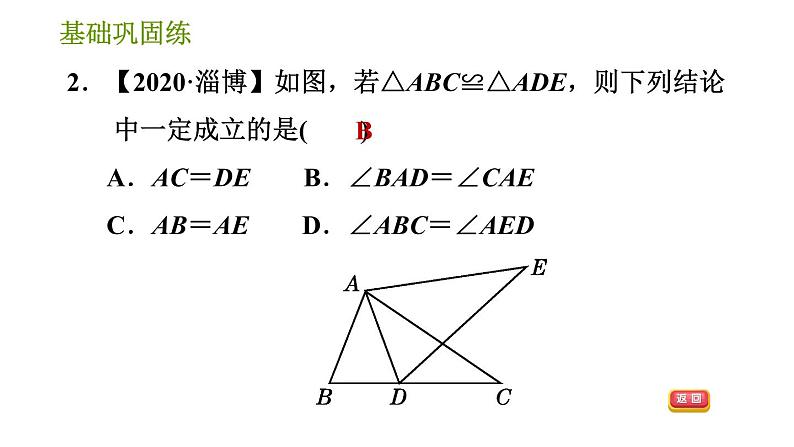
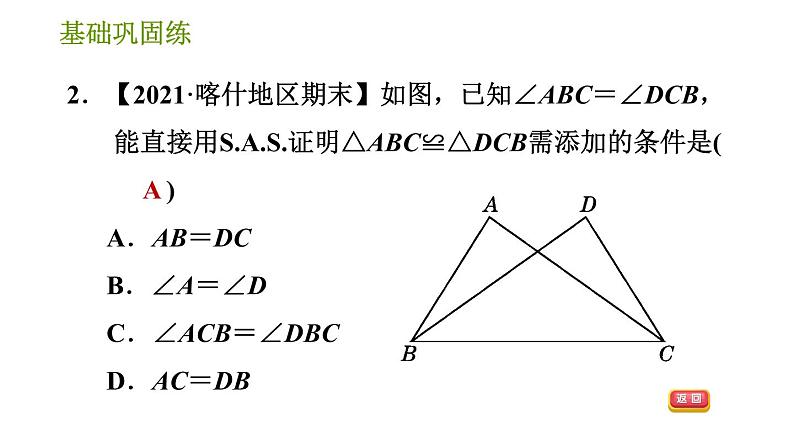
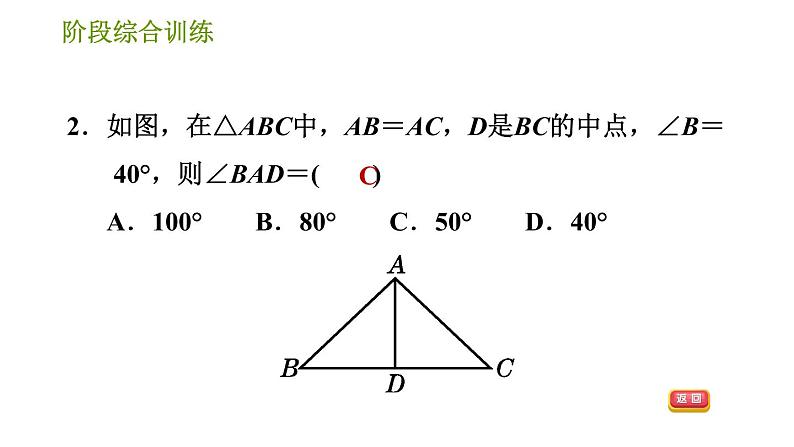
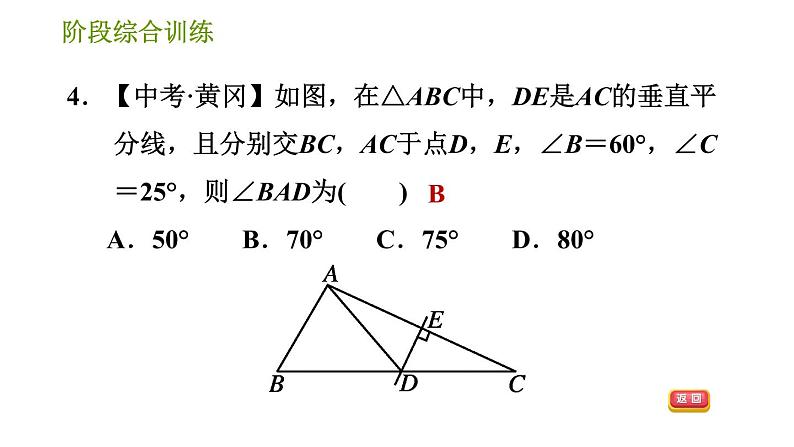
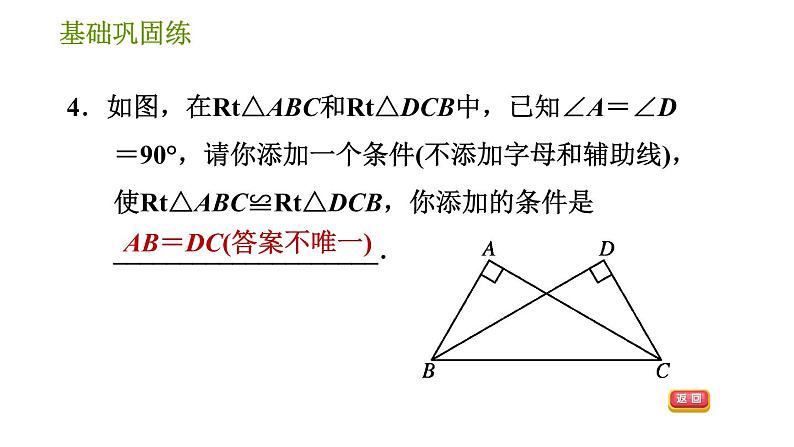
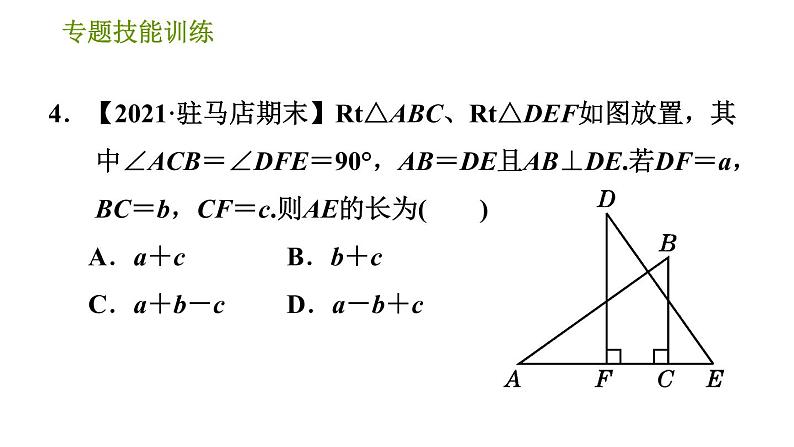
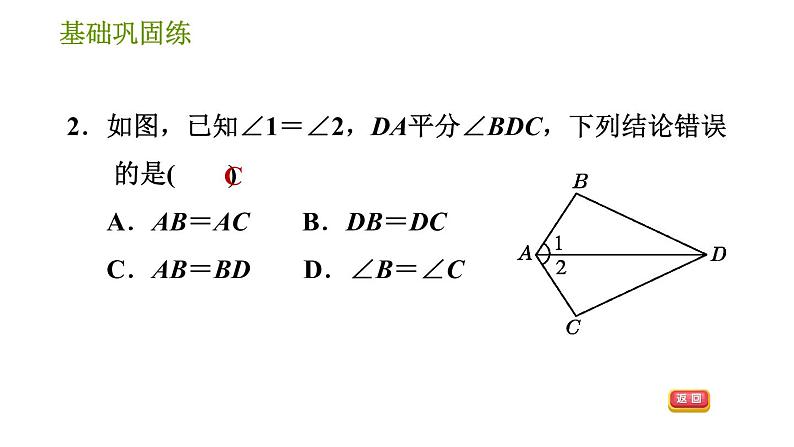
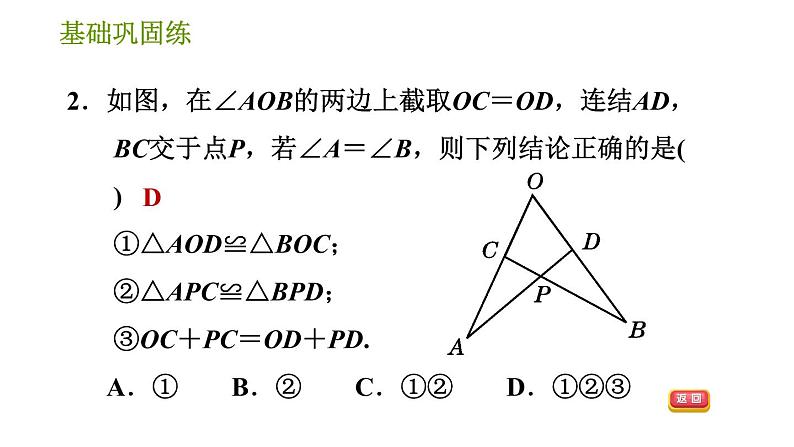
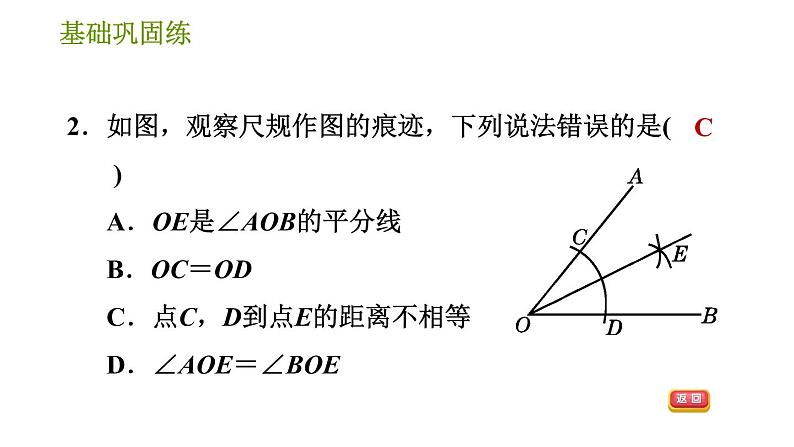
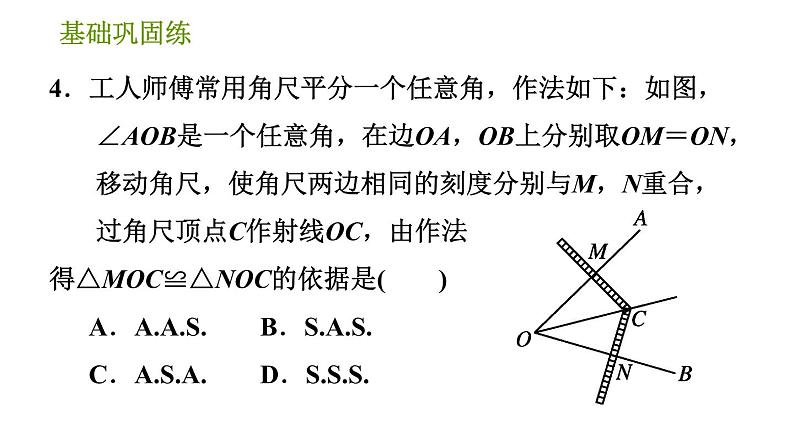
2.【2021·喀什地区期末】如图,已知∠ABC=∠DCB,能直接用证明△ABC≌△DCB需添加的条件是( ) A.AB=DC B.∠A=∠D C.∠ACB=∠DBC D.AC=DB
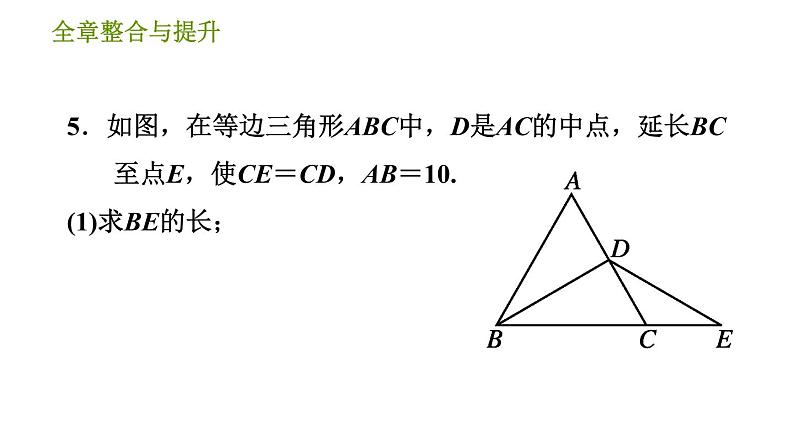
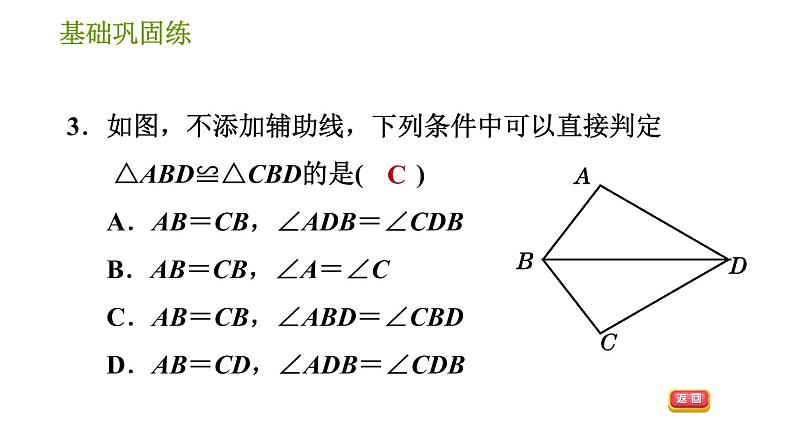
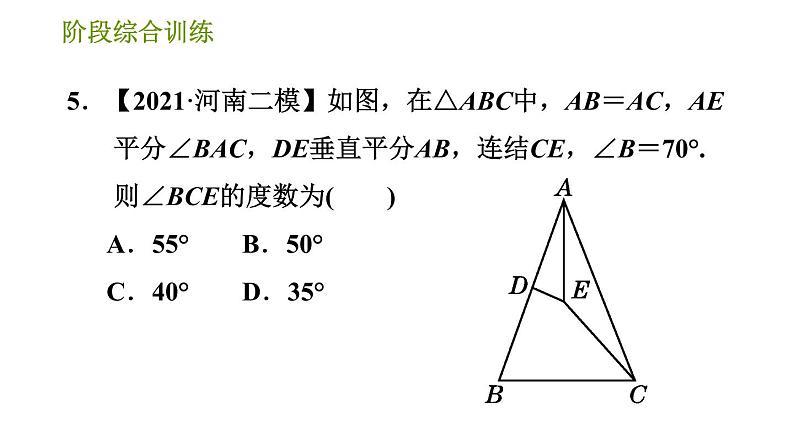
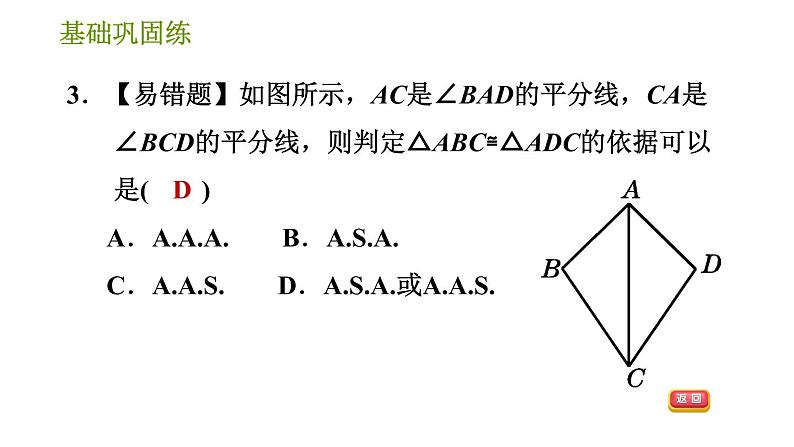
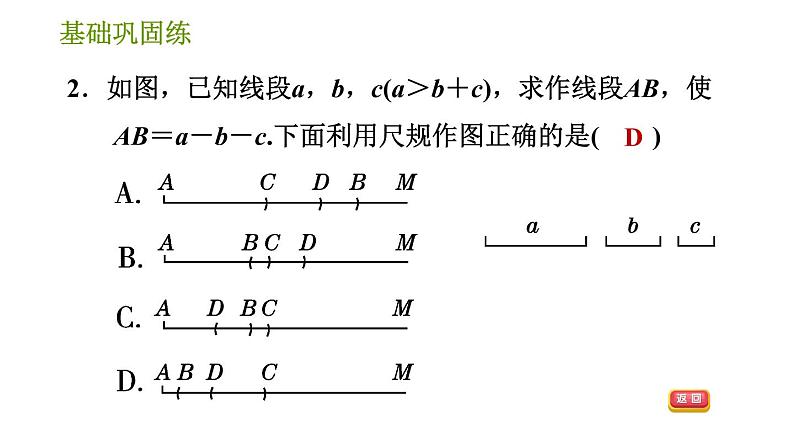
3.如图,不添加辅助线,下列条件中可以直接判定△ABD≌△CBD的是( ) A.AB=CB,∠ADB=∠CDB B.AB=CB,∠A=∠C C.AB=CB,∠ABD=∠CBD D.AB=CD,∠ADB=∠CDB
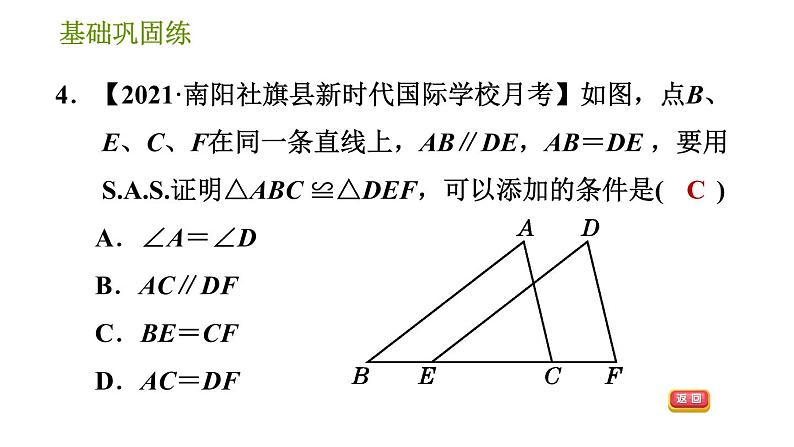
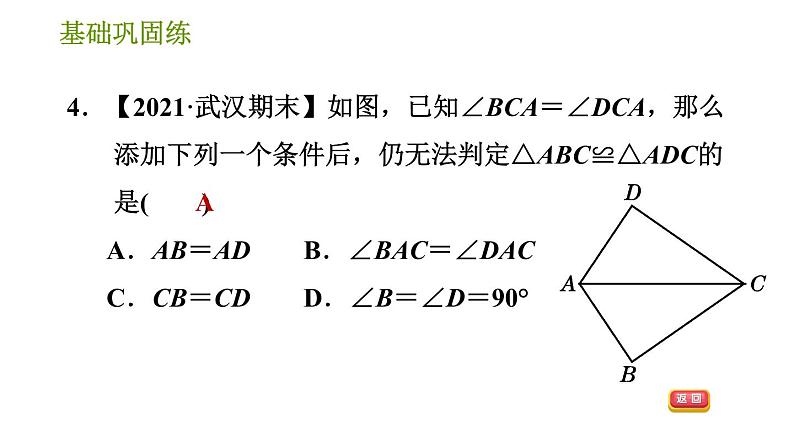
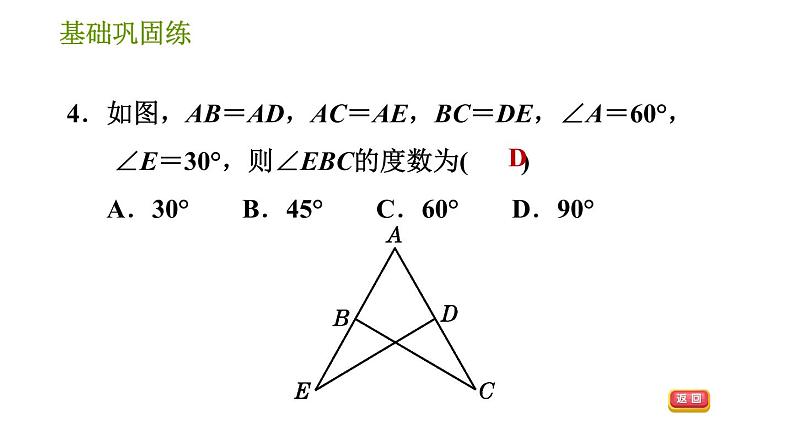
4.【2021·南阳社旗县新时代国际学校月考】如图,点B、E、C、F在同一条直线上,AB∥DE,AB=DE ,要用证明△ABC ≌△DEF,可以添加的条件是( ) A.∠A=∠D B.AC∥DF C.BE=CF D.AC=DF
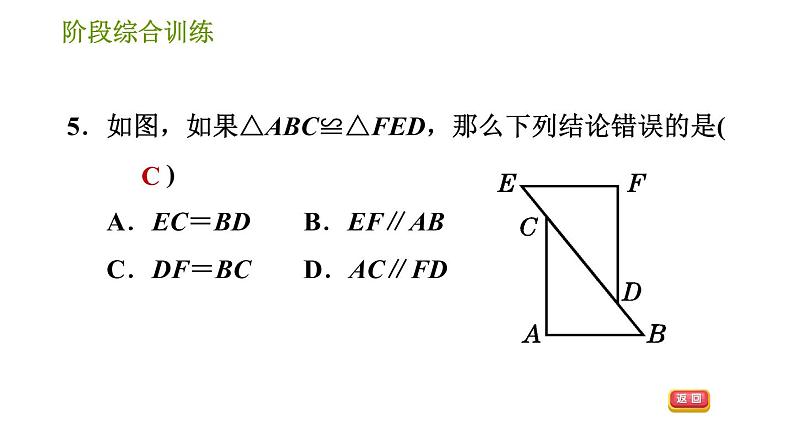
5.如图,已知AB=AC,E是角平分线AD上任意一点,则图中全等三角形共有( ) A.0对 B.1对 C.2对 D.3对
6.如图,AO是∠BAC和∠DAE的平分线,AD=AE,AB=AC,则线段BD和CE的大小关系是( ) A.BD>CE B.BD=CE C.BD
8.如图,已知∠1=∠2,AB=AD,AE=AC,若∠B=30°,则∠D的度数为________.
9.【中考·南京】如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是________.
10.【2020·吉林】如图,在△ABC中,AB>AC,点D在边AB上,且BD=CA,过点D作DE∥AC,并且使DE=AB,且点C,E在AB同侧,连结BE.求证:△DEB≌△ABC.
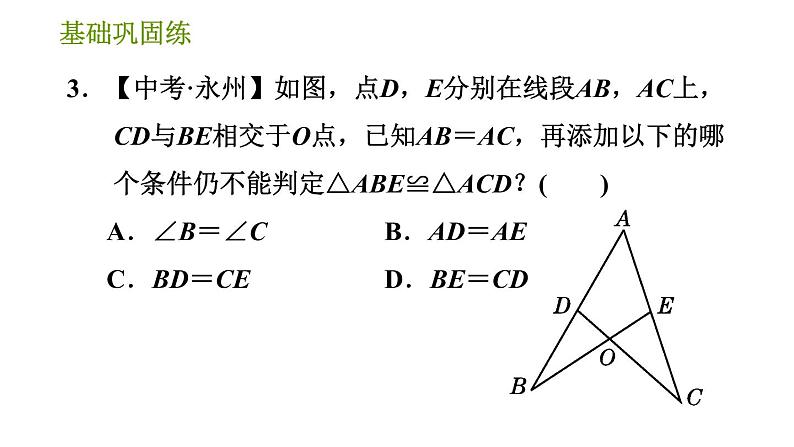
11.【2020·无锡】如图,已知AB∥CD,AB=CD,BE=CF.求证:(1)△ABF≌△DCE;
证明:∵△ABF≌△DCE,∴∠AFB=∠DEC,∴∠AFE=∠DEF,∴AF∥DE.
12.如图,AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
13.【中考·湘潭】如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数.
解:由(1)知,△DAF≌△ABE,∴∠ADF=∠BAE.∵∠ADF+∠DAO=∠BAE+∠DAO=∠DAB=90°,∴∠AOD=180°-(∠ADF+∠DAO)=90°.
14.如图,AD是△ABC中BC边上的中线.
八年级上册第14章 勾股定理综合与测试习题ppt课件: 这是一份八年级上册第14章 勾股定理综合与测试习题ppt课件,文件包含华师版八年级上册数学习题课件第14章14111直角三角形三边的关系1ppt、华师版八年级上册数学习题课件第14章14112直角三角形三边的关系2ppt、华师版八年级上册数学习题课件第14章1412直角三角形的判定ppt、华师版八年级上册数学习题课件第14章1413反证法ppt、华师版八年级上册数学习题课件第14章1421勾股定理的应用1ppt、华师版八年级上册数学习题课件第14章1422勾股定理的应用2ppt、华师版八年级上册数学习题课件第14章专题技能训练四训练勾股定理的综合应用ppt、华师版八年级上册数学习题课件第14章全章整合与提升ppt、华师版八年级上册数学习题课件第14章阶段综合训练范围1411~142ppt等9份课件配套教学资源,其中PPT共246页, 欢迎下载使用。
华师大版八年级上册第15章 数据的收集与表示综合与测试习题课件ppt: 这是一份华师大版八年级上册第15章 数据的收集与表示综合与测试习题课件ppt,文件包含华师版八年级上册数学习题课件第15章151数据的收集ppt、华师版八年级上册数学习题课件第15章1521扇形统计图ppt、华师版八年级上册数学习题课件第15章1522利用统计图表传递信息ppt、华师版八年级上册数学习题课件第15章专题技能训练五训练利用统计图获取信息ppt、华师版八年级上册数学习题课件第15章全章整合与提升ppt、华师版八年级上册数学习题课件第15章阶段综合训练范围151~1522ppt等6份课件配套教学资源,其中PPT共141页, 欢迎下载使用。
数学八年级上册第13章 全等三角形13.1 命题、定理与证明1 命题习题ppt课件: 这是一份数学八年级上册第13章 全等三角形13.1 命题、定理与证明1 命题习题ppt课件,共27页。PPT课件主要包含了答案显示,见习题,新知笔记,a2b2,两个角是锐角,两个角的和是钝角,AB∥CD,∠A=53°,∠CDA=53°等内容,欢迎下载使用。













