人教版新课标A必修13.2.1几类不同增长的函数模型背景图课件ppt

这是一份人教版新课标A必修13.2.1几类不同增长的函数模型背景图课件ppt，共14页。PPT课件主要包含了问题提出，理论迁移等内容，欢迎下载使用。

1.指数函数y=ax (a>1)，对数函数 y=lgax(a>1)和幂函数y=x n (n>0)在区间（0，+∞）上的单调性如何？
2.利用这三类函数模型解决实际问题，其增长速度是有差异的，我们怎样认识这种差异呢？
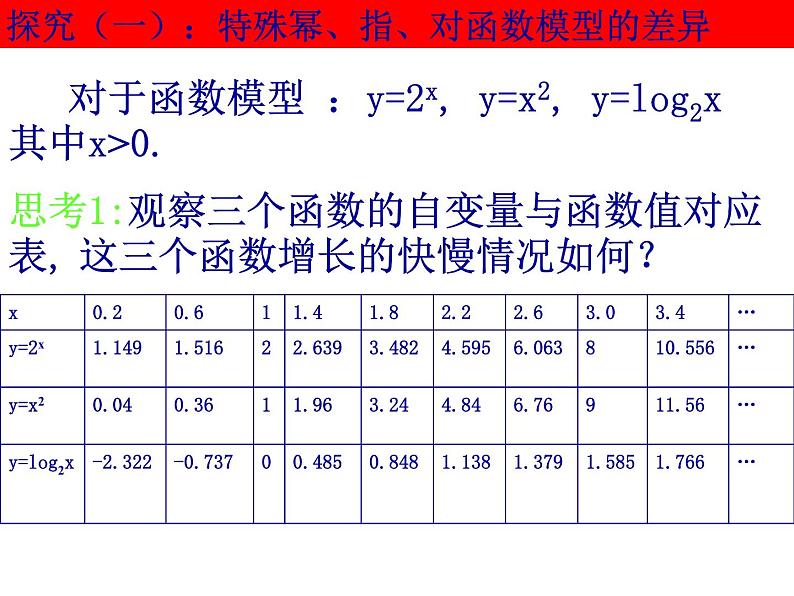
探究（一）：特殊幂、指、对函数模型的差异
对于函数模型 ：y=2x, y=x2, y=lg2x 其中x>0.
思考2:对于函数模型y=2x和y=x2，观察下列自变量与函数值对应表：
当x>0时，你估计函数y=2x和y=x2的图象共有几个交点？
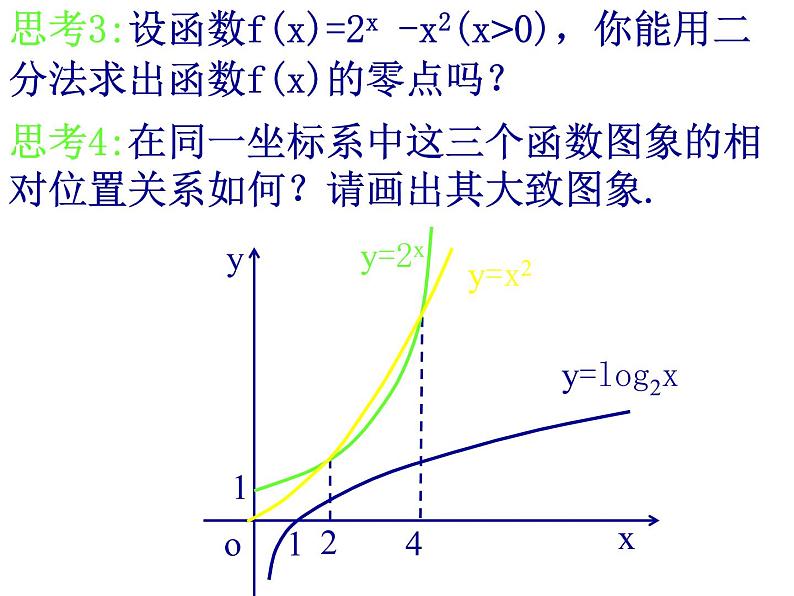
思考4:在同一坐标系中这三个函数图象的相对位置关系如何？请画出其大致图象.
思考3:设函数f(x)=2x -x2(x>0)，你能用二分法求出函数f(x)的零点吗？
思考5:根据图象，不等式lg2x<2x思考6:上述不等式表明，这三个函数模型增长的快慢情况如何？
探究（二）：一般幂、指、对函数模型的差异
思考1:对任意给定的a>1和n>0，在区间(0,+∞)上ax是否恒大于xn? ax是否恒小于xn?
思考2:当a>1，n>0时，在区间(0,+∞)上, ax与xn的大小关系应如何阐述？
思考3:一般地，指数函数y=ax (a>1)和幂函数y=xn(n>0)在区间(0,+∞)上，其增长的快慢情况是如何变化的？
思考4:对任意给定的a>1和n>0，在区间 (0,+∞)上,lgax是否恒大于xn? lgax是否恒小于xn?
思考5:随着x的增大,lgax增长速度的快慢程度如何变化? xn增长速度的快慢程度如何变化？
思考6:当x充分大时,lgax(a>1)xn与(n>0)谁的增长速度相对较快？
思考7:一般地，对数函数y=lgax(a>1)和幂函数y=xn(n>0) 在区间(0,+∞)上，其增长的快慢情况如何是如何变化的？
思考8:对于指数函数y=ax(a>1)，对数函数 y=lgax(a>1)和幂函数y=xn(n>0)，总存在一个x0，使x>x0时,ax,lgax,xn三者的大小关系如何？
思考9:指数函数y=ax (0 例 在某种金属材料的耐高温实验中，温度y(°C)随着时间t(分钟)的变化情况，由微机处理后显示出如下图象，试对该实验现象作出合理解释.