2021学年第三章 函数的应用综合与测试图文课件ppt

这是一份2021学年第三章 函数的应用综合与测试图文课件ppt，共41页。PPT课件主要包含了连续不断，fc0，典例分析，举一反三，答案C，基础梳理，逐步逼近，在a与b之间，增函数，越来越快等内容，欢迎下载使用。

f(a)·f(b)<0
题型一 求函数零点
分析 根据函数零点与相应方程的根之间的关系，就是求该函数相对应的方程的根.
题型二 判断方程零点个数
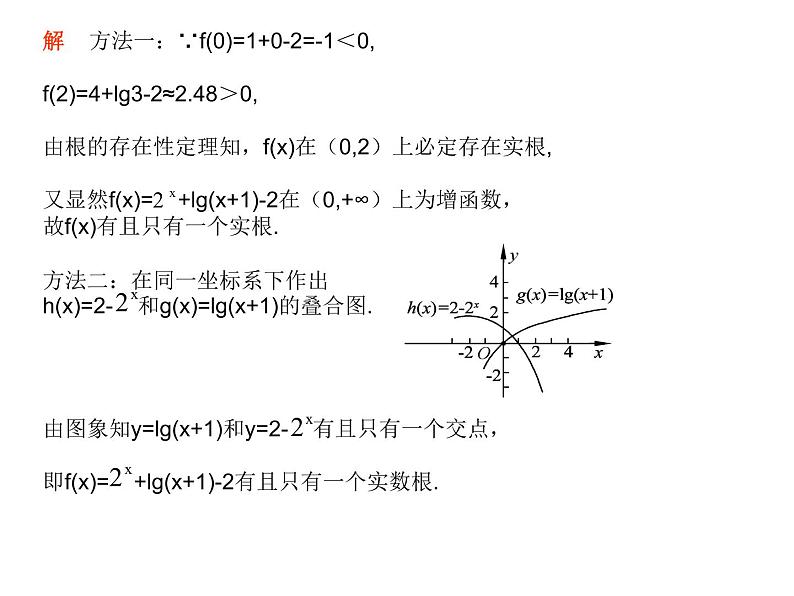
分析 判定复合函数f(x)=g(x)-h(x)的零点个数问题，解答本题可采用数形结合的方法.
题型三 判断函数零点所在大致区间
例3方程lg3x+x=3的解所在的区间为（） A. (0，2) B. (1,2) C. (2,3) D. (3,4)
分析 构造函数并转化为确定函数的零点位于的区间，令f(x)=lg3x+x-3，则f(2)=lg32+2-3=lg3 <0，f(3)=lg33+3-3=1>0,那么方程lg3x+x=3的解所在的区间为(2,3).
第2课时 用二分法求方程的近似解
f(a)及f(b)的符号相反（a＜b），
f(a)·f(b)＜0
题型一 求方程近似解
解 由于f（-2）=-1＜0,f(-3)=4＞0，故取区间［-3,-2］作为计算的初始区间,用二分法逐次计算，列表如下 ：
根据上表计算知，区间［-2.25,-2.187 5］的长度是0.062 5＜0.1，所以函数的负零点可取-2.1875.
例2 利用计算器求方程lg x=3-x的近似解.（精确度0.1）
分析 本例是超越方程根的求解，而且是求近似值，故解答本题可采用二分法逐步逼近.
由于|2.625-2.562 5|=0.062 5＜0.1,所以原方程的近似解可取2.562 5.
题型二 用二分法解决实际问题
例3 在一个风雨交加的夜里，从某水库闸房到防洪指挥部的电话线路发生了故障，这是一条10 km长的线路，如何迅速查出故障所在？如果沿着线路一小段一小段查找，困难很多，每查一个点要爬一次电线杆，10 km长大约有200多根电线杆.想一想，维修线路的工人师傅怎样工作最合理？
分析 可以利用二分法的原理进行查找.
由于区间［1.257 812 5,1.265 625］的长度1.265 625-1.257 812 5=0.007 812 5＜0.01,1.265 625是函数零点的近似值，即32的近似值是1.265 625.
第3课时 几类不同增长的函数模型
1. 三种函数模型的性质
题型一 一次函数模型问题
例1 为了发展电信事业方便用户，电信公司对移动电话采用不同的收费方式，其中所使用的“便民卡”与“如意卡”在某市范围内每月(30天）的通话时间x（分）与通话费y（元）的关系如下图所示：
分析 由图象可知，函数模型为直线型，可用待定系数法先设出函数，再求出解析式，然后比较大小.
1. “依法纳税是每个公民应尽的义务”，国家征收个人工资、薪金所得税是分段计算的：总收入不超过1 600元的，免征个人工资、薪金所得税；超过1 600元部分需征税，设全月纳税所得额（所得额指工资、薪金中应纳税的部分）为x，x=全月总收入-1 600元,税率见下表：
（1）设应纳税额f(x），试用分段函数表示1~3级纳税额f(x)的 计算公式；（2）某人2007年10月份工资总收入为4 200元，试计算这个人10月份应纳个人所得税多少元？
(2)这个人10月份纳税所得额x=4 200-1 600=2 600,f(2 600)=0.15×2 600-125=265.
答：这个人10月份应缴纳个人所得税265元.
题型二 指数函数模型问题
例2 按复利计算利率的一种储蓄，本金为a元，每期利率为r，设本利和为y，存期为x，写出本利和y随存期x变化的函数式.如果存入本金1 000元，每期利率2.25%,试计算5期后的本利和是多少.
分析 复利是把前一期的本息加在一起作为下一期的本金.先求出函数解析式，再求函数值.
2. 某企业计划发行企业债券，每张债券现值500元，按年利率6.5%的复利计息，问:多少年后每张债券一次偿还本利和约1 000元？（lg 2≈0.301 0，lg 1.065≈0.027 3）
答：11年后每张债券一次偿还本利和约1 000 元.
题型三 分段函数模型问题
分析 阴影部分随着t的增加而变化，直线过A点前后阴影部分的几何形状不一样，因此应分段求出面积、表达式，然后合成一个分段函数.
3. 某人开车以50 km/h速度从A地出发，出发后1小时，因车坏停留2小时修车，修好后以80 km/h的速度行驶，2小时后到达B地，再以70 km/h的速度返回A地.把车速v（km/h）表示为时间t（h）的函数，并画出函数的图象.
第4课时 函数模型的应用实例
题型一 已知函数模型的应用题
分析 解答本题可先列方程组求出待定系数，进而确定函数关系式，最后再求具体的函数值.
1. 如图是一份从2000年初到2003年初的统计图表，根据此图表得到以下说法中，正确的有（）
①这几年人民生活水平逐年得到提高;②人民生活费收入增长最快的一年是2000年;③生活价格指数上涨速度最快的一年是2001年;④虽然2002年生活费收入增长较缓慢，但由于生活价格指数也略有降低，因而人民生活有较大的改善.A. 1项B. 2项C. 3项D. 4项
解析: 根据图象,“生活费收入指数”减去“生活价格指数”的差是逐年增大的，故①正确.“生活费收入指数”2000—2001年最“陡”,故②正确.生活价格指数下降，而“生活费收入指数”曲线呈上升趋势，故③正确.
题型二 自建函数模型的应用题
例2 某市原来民用电价为0.52元/kW·h,换装分时电表后，峰时段(早上八点到晚上九点）的电价为0.55元/kW·h，谷时段（晚上九点到次日早上八点）的电价为0.35元/kW·h.对于一个平均每月用电量为200 kW·h的家庭，要使节省的电费不少于原来电费的10%,则这个家庭每月在峰时段的平均用电量至多为多少kW·h?
分析 先求出原来用电的费用，再设出峰时段的用电量建立不等式求解.
解 原来电费y1=0.52×200=104(元).设峰时段用电量为x kW·h，谷时段用电量为(200-x)kW·h,电费为y.则y=x×0.55+(200-x)×0.35≤(1-10%)y1,即0.55x+70-0.35x≤93.6,0.2x≤23.6,∴x≤118.即这个家庭每月在峰时段的平均用电量至多为118 kW·h.
其中x是仪器的月产量.当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)
答：当每月生产300台仪器时,利润最大,最大利润为25 000元.
题型三 函数拟合问题
例3 我国1999年至2002年国内生产总值（单位：万亿元）如下表所示：
(1)画出(x,y)的散点图，近似地写出一个函数关系式；(2)利用得出的关系式检验表中未用数据；（3）利用得出的关系式预测2003年我国的国内生产总值.
分析 该题要根据散点图选择一个函数近似反映y与x的关系，并利用所求的拟合函数进行验证、预测.
解 （1）画散点图略.从图形可以看出，四个点近似地落在一条直线上，设所求函数为y=kx+b.选择两点(0,8.206 7)和(3,10.239 8)代入，解方程组得k=0.677 7, b=8.206 7.因此所求函数关系式为y=f(x)=0.677 7x+8.206 7.(2) f(1)=0.677 7×1+8.206 7=8.884 4,f(2)=0.677 7×2+8.206 7=9.562 1.与表中相应函数值相比，误差不超过0.1.
（3）2003年，即x=4时，有f(4)=0.677 7×4+8.206 7=10.917 5.
答：可以预测2003年国内生产总值约为10.917 5万亿元.