易错题复习——与函数有关的动点问题

这是一份易错题复习——与函数有关的动点问题，共26页。试卷主要包含了如图，点A是反比例函数y═，如图，点A是反比例函数y，如图，点A的坐标为等内容，欢迎下载使用。

易错题复习——与函数有关的动点问题
1.如图，若点P为函数 图象上的一动点， 表示点P到原点O的距离，则下列图象中，能表示 与点P的横坐标 的函数关系的图象大致是（    ）

     
A.                                          B. 
C.                                       D. 
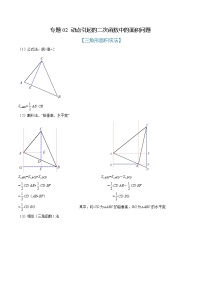
2.如图①，在 中，动点 从点 出发，沿折线 运动，设点 经过的路程为 的面积为 ，把 看做 的函数，函数的图像如图②所示，则图②中a的值等于（   ）

A.                                       B.                                       C. 14                                      D. 18
3.如图，已知线段AB＝12厘米，动点P以2厘米/秒的速度从点A出发向点B运动，动点Q以4厘米/秒的速度从点B出发向点A运动.两点同时出发，到达各自的终点后停止运动.设两点之间的距离为s(厘米)，动点P的运动时间为t秒，则下图中能正确反映s与t之间的函数关系的是(    )

A.                                            B. 
C.                                            D. 
4.如图，正方形 的边长为 ，动点 从点 出发以 的速度沿着边 运动，到达点 停止运动，另一动点 同时从点 出发，以 的速度沿着边 向点 运动，到达点 停止运动，设点 运动时间为 ， 的面积为 ，则 关于 的函数图象是（   ）

A.                                   B. 
C.                                   D. 
5.如图，点A是反比例函数y═ （x＞0）上的一点，过点A作AC⊥y轴，垂足为点C，AC交反比例函数y＝ 的图象于点B，点P是x轴上的动点，则△PAB的面积为（   ）

A. 2                                           B. 4                                           C. 6                                           D. 8
6.如图，点A是反比例函数y （x＞0）上的一点，过点A作AC⊥y轴，垂足为点C，AC交反比例函数y＝ 的图象于点B，点P是x轴上的动点，则△PAB的面积为（   ）

A. 2                                           B. 4                                           C. 6                                           D. 8
7.如图，在矩形 中， ， ，动点P沿折线 从点B开始运动到点D，设点P运动的路程为 ， 的面积为y，那么y与x之间的函数关系的图象大致是   

A.                                        B.   
C.                                       D. 
8.如图，已知A,B是反比例函数 图象上的两点， 轴，交x轴于点C.动点P从坐标原点O出发，沿 匀速运动，终点为C.过点P作 轴于Q.设 的面积为S,点P运动的时间为t则S关于t的函数图象大致为（   ）

A.                                        B. 
C.                                         D. 
9.如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作等腰直角△ABC，使∠BAC=90°，如果点B的横坐标为x，点C的纵坐标为y，那么表示y与x的函数关系的图像大致是（    ）

A.         B.         C.         D. 
10.如图，正方形ABCD的边长为2，动点P从点D出发，沿折线D→C→B作匀速运动，则△APD的面积S与点P运动的路程x之间的函数图象大致是（　　）

A.              B.              C.              D. 
11.如图，点P是▱ABCD边上的一动点，E是AD的中点，点P沿E→D→C→B的路径移动，设P点经过的路径长为x，△BAP的面积是y，则下列能大致反映y与x的函数关系的图象是（   ）

A.           B.           C.           D. 
12.如图①，在长方形MNPQ中，动点R从点N出发，沿N→P→Q→M方向运动至点M处停止．设点R运动的路程为x ， △MNR的面积为y ， 如果y关于x的函数图像如图②所示，则当x＝9时，点R应运动到(    )

A. M处                                      B. N处                                      C. P处                                      D. Q处
13.如图，一次函数与反比例函数的图象交于A（1，8）和B（4，2）两点，点P是线段AB上一动点（不与点A和B重合），过P点分别作x轴，y轴的垂线PC，PD交反比例函数图象于点E，F，则四边形OEPF面积的最大值是（    ）

A. 3                                           B. 4                                           C.                                            D. 6
14.如图①，在菱形 中，动点P从点B出发，沿折线 运动.设点P经过的路程为x， 的面积为y.把y看作x的函数，函数的图象如图②所示，则图②中的b等于________.

15.已知二次函数y＝ax2＋bx＋6的图像开口向下，与x轴交于点A（－6，0）和点B（2，0），与y轴交于点C，点P是该函数图像上的一个动点（不与点C重合）

（1）求二次函数的关系式；
（2）如图1当点P是该函数图像上一个动点且在线段 的上方，若△PCA的面积为12，求点P的坐标；
（3）如图2，该函数图像的顶点为D，在该函数图像上是否存在点E，使得∠EAB＝2∠DAC，若存在请直接写出点E的坐标；若不存在请说明理由.
16.如图，在平面直角坐标系中，一次函数图象与x轴，y轴分别交于点A（8，0），B（0，4），点C的坐标为（3，0），动点D是射线BO上一个动点，连结CD，过点C作CD⊥FC，交一次函数图象于点F．


（1）
求这个一次函数的解析式；


（2）过点F作FE⊥x轴，垂足为点E，当△OCD与△EFC全等时，求出满足条件的点F的坐标；


（3）点D在运动过程中，是否存在使△ACF是等腰三角形？若存在请求出点F的坐标；不存在，请说明理由．
19.已知，一次函数 的图像与 轴、 轴分别交于点A、点B，与直线  相交于点C.过点B作 轴的平行线l.点P是直线l上的一个动点.

（1）求点A，点B的坐标.
（2）若 ，求点P的坐标.
（3）若点E是直线 上的一个动点，当△APE是以AP为直角边的等腰直角三角形时，求点E的坐标.
20.在平面直角坐标系中，二次函数y＝ x2+bx+c的图象与x轴交于A(﹣2，0)，B(4，0)两点，交y轴于点C，点P是第四象限内抛物线上的一个动点.

（1）求二次函数的解析式；
（2）如图甲，连接AC，PA，PC，若 ，求点P的坐标；
（3）如图乙，过A，B，P三点作⊙M，过点P作PE⊥x轴，垂足为D，交⊙M于点E.点P在运动过程中线段DE的长是否变化，若有变化，求出DE的取值范围；若不变，求DE的长.
21.用函数方法研究动点到定点的距离问题．
在研究一个动点P（x，0）到定点A（1，0）的距离S时，小明发现：
S与x的函数关系为S＝ 并画出图像如图：

借助小明的研究经验，解决下列问题：
（1）写出动点P（x，0）到定点B（－2，0）的距离S的函数表达式，并求当x取何值时，S取最小值？
（2）设动点P（x，0）到两个定点M（1，0）、N（5，0）的距离和为y．
①随着x增大，y怎样变化？
②当x取何值时，y取最小值，y的最小值是多少？
③当x