


人教B版 (2019)必修 第四册第十一章 立体几何初步11.1 空间几何体11.1.3 多面体与棱柱课文内容课件ppt
展开日常生活中常见到一些多面体,如棱柱,棱锥,棱台.它们可以是我们日常用到的物品,也可以是建筑物的形状.你能说出各种几何体的特征吗?
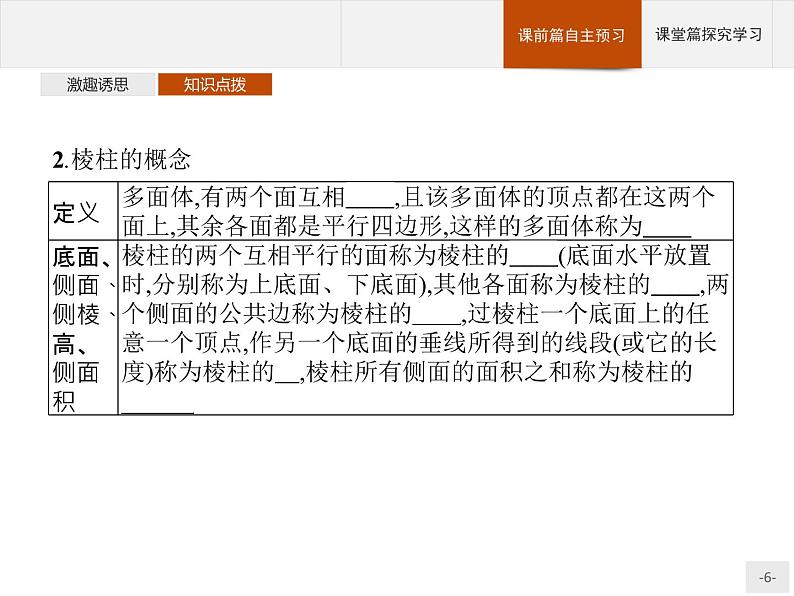
知识点一:多面体与棱柱1.多面体的概念
名师点析 1.如图,进一步了解多面体中的概念.
2.多面体至少有四个面、四个顶点、六条棱,并不是所有的多面体都有体对角线.3.面对角线和体对角线是两个不同的概念.
微思考1观察下面物体,你能说出各组图形的共同点吗?
提示:几何体的表面由若干个平面多边形围成.
微思考2观察下列多面体,有什么共同特点?
提示:有两个面相互平行;其余各面都是平行四边形;每相邻两个四边形的公共边都互相平行.
微思考3棱柱的侧面一定是平行四边形吗?提示:根据棱柱的特点知侧棱平行、底面平行,所以棱柱的侧面一定是平行四边形.微思考4多面体最少有几个面?多面体如何命名?提示:至少有4个面.多面体可以按照围成它的面的个数来命名.
微判断(1)棱柱的侧面可以不是平行四边形.( )(2)多面体的一个面可以是曲面.( )(3)棱柱的棱都相等.( )答案:(1)× (2)× (3)×
微练习1下面属于多面体的是 (填序号). ①建筑用的方砖;②埃及的金字塔;③球.答案:①②微练习2一个棱柱的侧面展开图是三个全等的矩形,每个矩形的长和宽分别为6 cm,4 cm,则该棱柱的侧面积为 . 答案:72 cm2解析:棱柱的侧面积S侧=3×6×4=72(cm2).
知识点二:棱锥与棱台1.棱锥的概念
微思考1观察下列多面体,有什么共同特点?
提示:有一个面是多边形;其余各面都是有一个公共顶点的三角形.
微思考2观察下列多面体,分析其与棱锥有何区别与联系?
提示:①区别:有两个面相互平行.②联系:用平行于棱锥底面的平面去截棱锥,其底面和截面之间的部分即为该几何体.
微思考3棱台的上、下底面互相平行,各侧棱延长线一定相交于一点吗?提示:根据棱台的定义可知其侧棱延长线一定交于一点.
微练习1在三棱锥A-BCD中,可以当作棱锥底面的三角形的个数为( ) A.1B.2C.3D.4答案:D解析:每个面都可作为底面,有4个.微练习2(多选题)棱台具备的特点是( )A.两底面相似B.侧面都是梯形C.侧棱都平行D.侧棱延长后都交于一点答案:ABD解析:由棱台的定义和结构特征知C为棱台不具备的特点.
微练习3下面各图形所表示的几何体中,不是棱锥的为( )
答案:A解析:A不符合棱锥定义,不是棱锥,B为四棱锥,C,D均为五棱锥.
多面体的识别与判断例1如图所示为长方体ABCD-A'B'C'D',当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由;如果是,指出底面及侧棱.
解:条件为一个长方体被一个平面所截,观察所得几何体上、下底面的关系与侧棱间的位置关系,抓住图中线段EF和B'C'的位置关系,根据定义得出结论.截面BCFE右侧部分是棱柱,因为它满足棱柱的定义.它是三棱柱BEB'-CFC',其中△BEB'和△CFC'是底面,EF,B'C',BC是侧棱.截面BCFE左侧部分也是棱柱.它是四棱柱ABEA'-DCFD',其中四边形ABEA'和四边形DCFD'是底面.A'D',EF,BC,AD为侧棱.
变式训练 1如图,已知长方体ABCD-A1B1C1D1,过BC和AD分别作一个平面交底面A1B1C1D1于EF,PQ,则长方体被分成的三个几何体中,棱柱的个数是 .
答案:3解析:由棱柱的定义可得有3个.
棱柱的结构特征例2(多选题)下列四个命题中,真命题为( )A.棱柱中两个互相平行的平面一定是棱柱的底面B.棱柱的各个侧面都是平行四边形C.棱柱的两底面是全等的多边形D.棱柱的面中,至少有两个面互相平行答案:BCD解析:A错,正六棱柱的两个相对的侧面互相平行,但不是棱柱的底面,B,C,D是正确的.
反思感悟 棱柱的性质(1)棱柱的各个侧面都是平行四边形,所有的侧棱都平行且相等;直棱柱的各个侧面都是矩形;正棱柱的各个侧面都是全等的矩形.(2)棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形.(3)过棱柱不相邻的两条侧棱的截面都是平行四边形.(4)直棱柱的侧棱长与高相等;直棱柱的侧面及经过不相邻的两条侧棱的截面都是矩形.
变式训练 2下列关于棱柱的性质正确的是( )A.只有两个面相互平行B.所有棱都相等C.所有面都是四边形D.各侧面都是平行四边形答案:D解析:棱柱的两个底面一定是平行的,但在棱柱中并不一定只有两个面相互平行,故A错;棱柱所有的侧棱长都相等,但它们不一定等于底面多边形的边长,故B错;棱柱的侧面都是四边形,但底面可以不是四边形,故C错;棱柱的所有侧面都是平行四边形,故D正确,选D.
棱锥、棱台的结构特征例3下列几种说法中,正确的有( )①用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;②棱台的侧面一定不会是平行四边形;③有两个面互相平行,其余四个面都是等腰梯形的六面体是棱台.A.0个B.1个C.2个D.3个
答案:B解析:必须用一个平行于底面的平面去截棱锥,棱锥底面和截面之间的部分才是棱台,故①不正确;棱台的侧面一定是梯形,故②正确;③不一定是棱台,因为各条侧棱延长后不一定相交于一点,故③不正确.
反思感悟 关于棱锥、棱台结构特征题目的判断方法(1)举反例法.结合棱锥、棱台的定义举反例判断关于棱锥、棱台结构特征的某些说法不正确.(2)直接法.
变式训练 3下列关于棱锥、棱台的说法:①棱台的底面一定不会是平行四边形;②棱锥的侧面只能是三角形;③由四个面围成的封闭图形只能是三棱锥;④棱锥被平面截成的两部分不可能都是棱锥.其中所有正确说法的序号是 .
解析:①不正确,棱台的底面可以是平行四边形还可以是其他多边形;②正确,由棱锥的定义知棱锥的侧面只能是三角形;③正确;④错误,如图所示四棱锥被平面截成的两部分都是棱锥.
多面体的侧面积或表面积例4(1)在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,∠AA1B1=∠AA1C1=60°,∠BB1C1=90°,侧棱长为b,则其侧面积为( )
(2)已知四棱锥S-ABCD的棱长均为5,底面为正方形,求它的侧面积和表面积.(3)已知正四棱台(上、下底是正方形,上底面的中心在下底面的投影是下底面的中心)上底面边长为6,高和下底面边长都是12,求它的侧面积.
解析:如图,由已知条件可知,侧面AA1B1B和侧面AA1C1C为一般的平行四边形,侧面BB1C1C为矩形.
(2)解:因为四棱锥S-ABCD的各棱长均为5,所以各侧面都是全等的正三角形.设E为AB的中点,连接SE,
(3)解:如图,E,E1分别是BC,B1C1的中点,O,O1分别是下、上底面正方形的中心,则O1O为正四棱台的高,则O1O=12.连接OE,O1E1,
变式训练 4(1)一个四棱台的上、下底面都为正方形,且上底面的中心在下底面的投影为下底面中心(即为正四棱台),两底面边长分别为1,2,侧面积等于两个底面积之和,则这个棱台的高为( )
(2)已知一个四棱锥底面为正方形,且顶点在底面正方形的投影为底面正方形的中心(即为正四棱锥),底面正方形的边长为4 cm,高与斜高的夹角为30°,如图所示,求正四棱锥的侧面积和表面积(单位:cm2).
提示:利用正棱锥的高、斜高、底面边心距组成的直角三角形求解,然后代入公式.
解析:如图所示,设O1,O分别为棱台的上、下底面中心,M1,M分别为B1C1,BC的中点,连接O1O,O1M1,OM,MM1,则M1M为斜高.过M1作M1H⊥OM于H点,则M1H=OO1,
(2)解:正棱锥的高PO、斜高PE、底面边心距OE组成Rt△POE.∵OE=2,∠OPE=30°,
多面体的表面展开图例5如图是三个几何体的表面展开图,请问各是什么几何体?
解:(1)五棱柱;(2)五棱锥;(3)三棱台.如图所示.
变式训练 5纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北,如下图①,现在沿该正方体的一些棱将正方体剪开,外面朝上展平,得到右侧的平面图形,如图②.则标“△”的面的方位是( )
A.南B.北C.西D.下
解析:将所给图形还原为正方体,如图所示,最上面为△,最左面为西,最里面为上,将正方体旋转后让左面向西,让“上”面向上可知标“△”的方位为南.
截面周长最小问题典例如图所示,在侧棱长为2 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF分别交VB,VC于点E,F,求截面△AEF周长的最小值.
分析将正三棱锥沿侧棱VA展开→求截面周长转化为求线段长→利用正三棱锥的性质求解
解:将三棱锥V-ABC沿侧棱VA剪开,将其侧面展开图平铺在一个平面上,如图所示,则△AEF的周长=AE+EF+FA1.因为AE+EF+FA1≥AA1,所以线段AA1(即A,E,F,A1四点共线时)的长即所求△AEF周长的最小值.作VD⊥AA1,垂足为点D.由VA=VA1,知D为AA1的中点.由已知∠AVB=∠BVC=∠CVA1=40°,得∠AVD=60°.
即AA1=2AD=6.所以截面△AEF周长的最小值是6.
方法点睛空间图形求表面上曲线段(或折线段)最小值的方法空间图形求表面上曲线段(或折线段)最小值时,关键是弄清几何体中的有关点、线在展开图中的相应位置关系.解决的方法就是把各侧面展开铺在平面上,根据“平面内连接两点的线段最短”来解决.借助平面几何的知识来解决立体几何中的问题,是处理立体几何问题的最佳方法.
1.给出下列命题:①有两个侧面是矩形的棱柱是直棱柱;②侧面都是等腰三角形的棱锥是正棱锥;③侧面都是矩形的直四棱柱是长方体;④若有两个侧面垂直于底面,则该四棱柱为直四棱柱;⑤各个面都是三角形的几何体是三棱锥.其中所有错误命题的序号是( )A.②③④B.①②③C.①②④D.①②③④⑤
答案:D解析:认识棱柱一般要从侧棱与底面的垂直与否和底面多边形的形状两方面去分析,故①③错误,对等腰三角形的腰是不是侧棱未作说明,故②错误,平行六面体的两个相对侧面也可能与底面垂直且互相平行,故④错误.由两个相同的三棱锥叠放在一起构成的几何体,它的各个面都是三角形,但它不是三棱锥,故⑤错误.
2.(多选题)如图所示,不是正四面体(正四面体是各棱长都相等的三棱锥)的展开图的是( )
答案:CD解析:可选择阴影三角形作为底面进行折叠,发现选项A,B可折成正四面体,选项C,D不论选哪一个三角形作底面折叠都不能折成正四面体.故选CD.
3.下列几何体中, 是棱柱, 是棱锥, 是棱台(填序号).
答案:①③④ ⑥ ⑤解析:结合棱柱、棱锥和棱台的定义可知①③④是棱柱,⑥是棱锥,⑤是棱台.
4.如图,将封闭的装有水的长方体水槽固定底面一边后将水槽倾斜一个角度,则倾斜后水槽中的水形成的几何体的形状是 .
答案:四棱柱(或三棱柱)解析:倾斜后水槽中水形成的几何体的形状应为四棱柱(或三棱柱).
5.(2020黑龙江牡丹江一中高一月考)如图,在正三棱柱A1B1C1-ABC中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且从点P沿棱柱侧面经过棱CC1到点M的最短路线长为 ,设这条最短路线与CC1的交点为N,求PC的长.
高中数学人教B版 (2019)必修 第四册11.1.4 棱锥与棱台教课内容ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册11.1.4 棱锥与棱台教课内容ppt课件,文件包含人教B版高中数学必修第四册第11章1114棱锥与棱台课件ppt、人教B版高中数学必修第四册第11章1114棱锥与棱台学案doc、人教B版高中数学必修第四册课后素养落实12棱锥与棱台含答案doc等3份课件配套教学资源,其中PPT共49页, 欢迎下载使用。
高中数学人教B版 (2019)必修 第四册11.1.4 棱锥与棱台评课ppt课件: 这是一份高中数学人教B版 (2019)必修 第四册11.1.4 棱锥与棱台评课ppt课件,共53页。PPT课件主要包含了多边形,有一个公共顶点,公共顶点,公共边,三棱锥,正多边形,底面中心,四棱台,正棱锥,棱锥的结构特征等内容,欢迎下载使用。
人教B版 (2019)11.1.3 多面体与棱柱教课内容ppt课件: 这是一份人教B版 (2019)11.1.3 多面体与棱柱教课内容ppt课件,共52页。PPT课件主要包含了平面多边形,各个多边形,公共边,公共点,不在同一面,同一面,平面图形,面积之和,都在这个平面的同一侧,都相等等内容,欢迎下载使用。













