小学数学人教版六年级上册1 圆的认识精品课时训练

这是一份小学数学人教版六年级上册1 圆的认识精品课时训练，共13页。试卷主要包含了【分析】根据圆周率的含义等内容，欢迎下载使用。

1.通过学生的画圆、剪圆、折圆等活动，使学生认识圆，发解圆的各部分名称，掌握圆的特征以及半径、直径的关系，理解圆心、半径、直径的作用。
2.在画圆、剪圆、折圆等活动中，培养学生的观察、分析、辨析、概括能力。
3.在活动中渗透普遍联系的辩证唯物主义观点。
教学重难点
掌握圆各部分的名称及圆的特征和圆的画法。
掌握圆各部分的名称及圆的特征和圆的画法。
复习巩固
【复习典例1】修一段路，已修的米数与未修的米数的比是4：3，已修的占全长的（ ）。
【复习典例2】饲养场鸡的只数比鸭少1200只，鸡与鸭的比是3：5，鸭有多少只？
【复习典例3】果园梨树与桃树的比是5：7，梨树有200棵，桃树有多少棵？
【复习典例4】 一种药水要按农药和水的重量比1：400配置成，则在240千克水中，应放入农药多少千克？
1、圆的定义：圆是由曲线围成的一种平面图形。
2、圆心：将一张圆形纸片对折两次，折痕相交于圆中心的一点，这一点叫做圆心。
一般用字母O表示。它到圆上任意一点的距离都相等.
3、半径：连接圆心到圆上任意一点的线段叫做半径。一般用字母r表示。
把圆规两脚分开，两脚之间的距离就是圆的半径。
4、直径：通过圆心并且两端都在圆上的线段叫做直径。一般用字母d表示。
直径是一个圆内最长的线段。
5、圆心确定圆的位置，半径确定圆的大小。
6、在同圆或等圆内，有无数条半径，有无数条直径。所有的半径都相等，所有的直径都相等。
7.在同圆或等圆内，直径的长度是半径的2倍，半径的长度是直径的 。
用字母表示为：d=2r或r =½d
8、轴对称图形：
如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形。
折痕所在的这条直线叫做对称轴。(经过圆心的任意一条直线或直径所在的直线)
9、长方形、正方形和圆都是对称图形，都有对称轴。这些图形都是轴对称图形。
10、只有1一条对称轴的图形有： 角、等腰三角形、等腰梯形、扇形、半圆。
只有2条对称轴的图形是： 长方形
只有3条对称轴的图形是： 等边三角形
只有4条对称轴的图形是： 正方形;
有无数条对称轴的图形是： 圆、圆环。
【题干1】要找到一张圆形纸片的圆心，至少要把它对折（ ）次．
A．3B．2C．1D．无数
【思路引导】圆中心的那个点即圆心，所有直径都相交于圆心，将一个圆形纸片最少要对折两次，才能找到两条折痕相交的那个点，即圆心．
【完整解答】将一个圆形纸片最少要对折两次，才能找到两条折痕相交的那个点，即圆心．
故选：B．
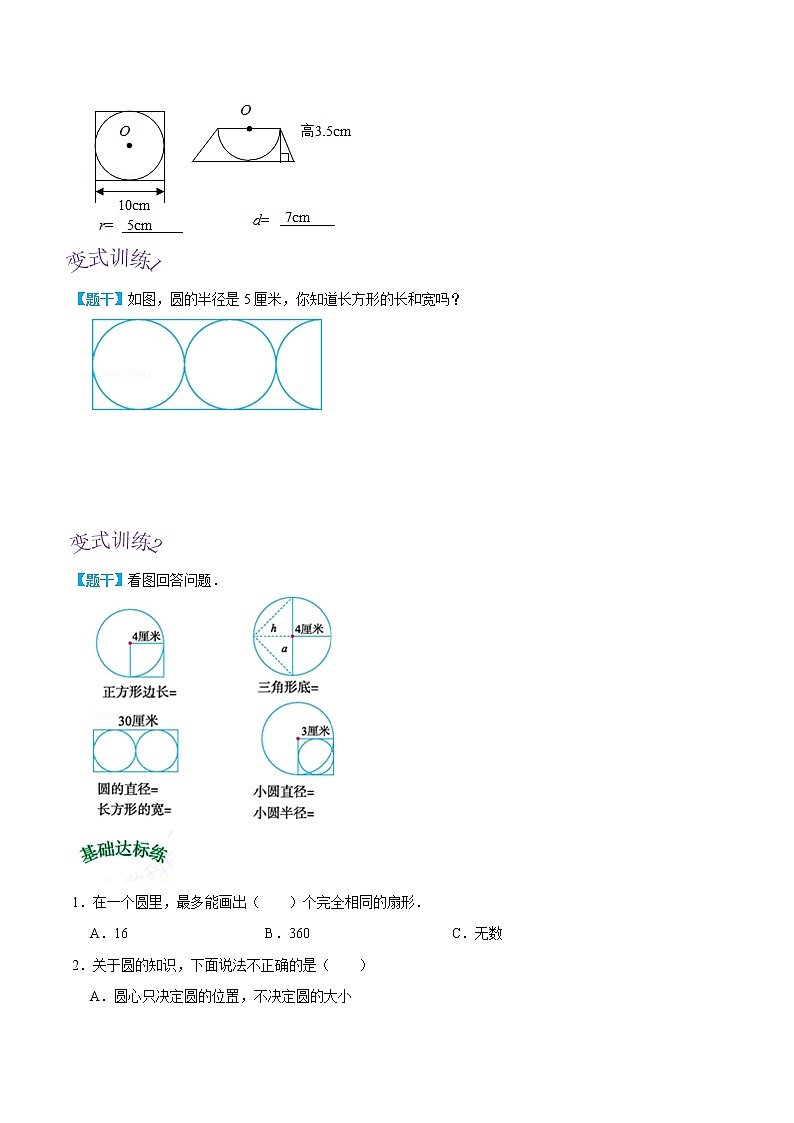
【题干2】看图填空
【思路引导】（1）已知直径是10厘米，根据r＝d÷2可求出半径；
（2）已知梯形的高是3.5厘米，也就是半径是3.5厘米，根据d＝2r可求出直径；
【完整解答】（1）10÷2＝5（厘米）
（2）3.5×2＝7（厘米）
【题干】如图，圆的半径是5厘米，你知道长方形的长和宽吗？
【题干】看图回答问题．
1．在一个圆里，最多能画出（ ）个完全相同的扇形．
A．16B．360C．无数
2．关于圆的知识，下面说法不正确的是（ ）
A．圆心只决定圆的位置，不决定圆的大小
B．两端都在圆上的线段叫做直径
C．半径相等的两个圆的面积相等
D．圆周率是圆周长和这个圆直径的比值
3．圆的大小与（ ）有关．
A．圆心B．半径C．圆周率
4．在一个正方形里画一个最大的圆，圆的 与正方形的 相等．在一个圆里画一个最大的正方形，正方形的 与圆的 相等．
5．在同圆内，半径是直径的 ，直径是半径的 ．
6．我国古代数学家刘徽利用 一直算到圆内接正一百九十二边形，得到圆周率的近似值是3.14．
7．圆的周长是直径的 倍，它是一个固定不变的数，把它叫做 ，用字母 表示．1500多年前，我国伟大的数学家 发现的．
8．圆的周长总是它直径的π倍． ． （判断对错）
9．圆内最长的线段是圆的直径． （判断对错）
10．知识全掌握，轻松填表格．
11．看图填空
圆的直径是 6 厘米，正方形的边长是 厘米．
12．画两个同心圆，第一个圆的直径为4厘米，第二个圆的直径比第一个圆大1厘米．
13．填一填．
1．如图．线段（ ）
A．a是直径B．b是半径C．c是半径D．b是直径
2．在一个长10厘米、宽4厘米的长方形里画一个最大的圆，这个圆的直径是（ ）
A．10厘米B．8厘米C．6厘米D．4厘米
3．看图填空．（单位：cm）
（小圆）r＝ cm
d＝ cm
4．

直径 cm．
5．
直径 cm．
6．
半径 cm．
7．在同圆或等圆中，直径都相等，半径也都相等 （判断对错）
8．量一量，画一画，算一算．
（1）量一量，图中半圆形的直径是 厘米．
（2）图中三角形ABC的面积是 平方厘米．
9．如图：圆的直径是 厘米，梯形的上底是 厘米，梯形的高是 厘米．
10．如图中，圆的半径是2.5厘米，圆的直径是 厘米，长方形的长是 厘米，宽是 厘米．你还能想到什么？
【复习巩固答案解析】
【复习典例1】
【思路引导】把已修的看成4份，那么未修的就是3份，总长度就是3份+4份=7份，再用已修的长度除以总长度即可。
【完整解答】4÷（3+4）=4÷7=；
答：已修的占全长的。
【复习典例2】
【思路引导】已知“鸡与鸭的比是3：5”，其中鸡的只数占总数的，鸭的只数占总数的，然后根据一个数除以分数的意义，用除法解答。
【完整解答】
答：鸭有3000只。
【复习典例3】
【思路引导】因为果园梨树与桃树的棵数比是5：7，则把梨树棵数看作5份的量，梨树棵数已知，从而可以求出1份的量，桃树是7份的量，进而可以求出桃树有多少棵。
【完整解答】
200÷5×7=280（棵）；
答：桃树有280棵。
【复习典例4】
【思路引导】根据农药和水的重量比是1：400，可设应放入农药千克，列出比例式：1：400=：240，得解。
【完整解答】
设应放入农药千克，根据题意得：
：240=1：400
400=240
=0.6
答：应放入农药0.6千克。
新知讲练答案解析
【变式训练1】
【思路引导】由图形可知：5个圆的半径的长等于长方形的长，2个圆的半径的长即长方形的宽，依此可求长方形的长和宽．
【完整解答】长方形的长：5×5＝25（厘米）
长方形的宽：5×2＝10（厘米）
答：长方形的长是25厘米，宽是10厘米．
【变式训练2】
【思路引导】（1）观察图形可知：半径的长等于正方形的边长；
（2）观察图形可知：三角形的底长即直径的长；
（3）观察图形可知：两条直径的长即30厘米，由此即可求出直径，长方形的宽等于圆的直径的长；
（4）观察图形可知：正方形的边长等于小圆直径的长，然后根据：r＝d÷2，解答即可．
【完整解答】如图所示：
基础达标练答案解析
1.【分析】一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形，据此判断即可．
【解答】解：因为一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形，
所以在一个圆里，最多能画出无数个完全相同的扇形．
故选：C．
2.【分析】根据题意，对各题进行依次分析、进而得出结论．
【解答】解：A、圆心只决定圆的位置，不决定圆的大小，说法正确；
B、两端都在圆上的线段叫做直径，说法错误，因为直径是经过圆心并且两端都在圆上的线段；
C、半径相等的两个圆，大小相等，所以的面积相等，说法正确；
D、圆周率是圆周长和这个圆直径的比值，说法正确；
故选：B．
3.【分析】根据“圆心决定圆的位置，半径决定圆的大小”进行判断即可．
【解答】解：因为圆心决定圆的位置，半径决定圆的大小；
所以得出：圆的大小与半径的长短有关；
故选：B．
4.【分析】通过观察图形，在一个正方形里画一个最大的圆，圆的直径与正方形的边关系，在一个圆里画一个最大的正方形，正方形的对角线的长度与圆的直径关系，由此解答即可。
【解答】解：在一个正方形里画一个最大的圆，圆的直径与正方形的边相等．在一个圆里画一个最大的正方形，正方形的对角线的长度与圆的直径相等。
故答案为：直径，边长，对角线的长度，直径。
5.【分析】依据圆的认识，及在同一个圆中半径与直径的关系：在同圆或等圆里，有无数条半径，无数条直径，直径是半径的2倍，半径相当于直径的一半；由此解答即可．
【解答】解：在同圆内，半径是直径的 一半，直径是半径的 2倍．
故答案为：一半，2倍．
6.【分析】根据教材中的课外阅读以及对圆周率知识的了解，进行解答即可．
【解答】解：我国古代数学家刘徽利用割圆术一直算到圆内接正一百九十二边形，得到圆周率的近似值
是3.14．
故答案为：割圆术．
7.【分析】圆周率（π）是一个常数（约等于3.141592654），是代表圆周长和直径的比值．它是一个无理数，即是一个无限不循环小数．但在日常生活中，通常都用3.14来代表圆周率去进行计算，即使是工程师或物理学家要进行较精密的计算，也只取值至小数点后约20位．
【解答】解：圆的周长是直径的3倍，它是一个固定不变的数，把它叫做圆周率，用字母π表示．1500多年前，我国伟大的数学家祖冲之发现的．
故答案为：3，圆周率，π，祖冲之．
8.【分析】根据圆周率的含义：圆的周长和它直径的比值，叫做圆周率；即圆的周长是直径的π倍；进而解答即可．
【解答】解：根据圆周率的含义，可得：圆的周长总是它直径的π倍；
所以原题的说法正确．
故答案为：√
9.【分析】通过圆心并且两端都在圆上的线段叫做直径．通过直径的定义可知，在一个圆中，圆内最长的线段一定是直径；由此判断．
【解答】解：通过直径的定义可知：在一个圆中，圆内最长的线段是圆的直径的说法是正确的；
故答案为：√．
10.【分析】根据同圆中d＝2r，r＝d÷2解答填表即可．
【解答】解：
直径/m
0.8
8.64
37
2
11.【分析】观察图形可得，正方形的边长等于圆的直径，圆的直径等于半径的2倍；据此即可求解．
【解答】解：
3×2＝6（厘米）
答：圆的直径是6厘米，正方形的边长是6厘米．
故答案为：6；6．
12.【分析】以固定一点为圆心，分别以4÷2＝2厘米和（4+1）÷2＝2.5厘米为半径画圆．
【解答】解：如图：4÷2＝2（厘米）
（4+1）÷2＝2.5（厘米）
13.【分析】（1）圆的直径已知，是8厘米，根据半径与直径的关系“r＝d÷2”即可求出圆的半径，然后填空即可．
（2）圆的半径已知，是3厘米，根据直径与半径的关系“d＝2r”即可求出圆的直径，然后填空即可．
（3）长方形的宽等于圆的直径，长等于圆直径的2倍，圆的半径已知，是1厘米，根据直径与半径的关系“d＝2r”即可求出圆的直径，即长方形的宽，长方形的宽乘2就是长方形的长．
【解答】解：填一填．
强化提优练答案解析
1.【分析】根据直径、半径的意义，通过圆心并且两端都在圆上的线段叫做直径，连接圆心和圆上任意一点的线段叫做半径．据此解答．
【解答】解：线段a、线段b虽然两端都在圆上，但是没有通过圆心．所以线段a、线段b不是直径；
线段c是连接圆心和圆上一点的线段，所以线段c是半径．
故选：C．
2.【分析】在一个长10厘米、宽4厘米的长方形里画一个最大的圆，这个圆的直径和长方形的宽相等时，这个圆最大．
【解答】解：在一个长10厘米、宽4厘米的长方形里画一个最大的圆，这个圆的直径是4厘米．
故选：D．
3.【分析】（1）大圆的直径是a厘米；根据半径＝直径÷2，求出大圆的半径，大圆的半径又是小圆的直径，所以大圆的半径再除以2，又是小圆的半径；
（2）根据图的读数，用圆右边的刻度减去圆左边的刻度就是这个圆直径的长度．
【解答】解：（1）a÷2÷2＝（cm）
（2）10.5﹣9＝1.5（cm）
故答案为：，1.5．
4.【分析】根据在同圆或等圆中，直径等于半径的2倍；由此解答即可．
【解答】解：3.5×2＝7（厘米）
答：直径是7厘米；
故答案为：7．
5.【分析】观察图形发现，圆的直径就是正方形的边长，所以圆的半径是8厘米．
【解答】解：圆的直径是8厘米．
故答案为：8．
6.【分析】根据在同圆或等圆中，半径是直径的一半解答即可．
【解答】解：4.2÷2＝2.1（厘米）
答：半径是2.1厘米．
故答案为：2.1．
7.【分析】根据圆的特征可知：在同圆或等圆中，同一圆里，所有的直径都相等，所有的半径也相等；进而判断即可．
【解答】解：在同圆或等圆中，直径都相等，半径也都相等，说法正确；
故答案为：√．
8.【分析】（1）经过测量可知，这个半圆的直径是4厘米，
（2）利用三角形的面积公式即可解答．
【解答】解：（1）经过测量可知，半圆的直径是4厘米，则半径是4÷2＝2厘米；
（2）三角形ABC的面积是：4×2÷2＝4（平方厘米），
答：三角形的面积是4平方厘米．
故答案为：4．
9.【分析】连接圆心和圆上任意一点的线段叫做半径．通过圆心，并且两端都在圆上的线段，叫做直径；观察图形可得：梯形的上底等于圆的直径，高等于圆的半径，据此根据“d＝2r”解答即可．
【解答】解：
4×2＝8（厘米）
答：圆的直径是8厘米，梯形的上底是8厘米，梯形的高是4厘米．
故答案为：8，8，4．
10.【分析】根据：d＝2r，求出圆的直径；由图形可知：5个圆的半径的长等于长方形的长，2个圆的半径的长即长方形的宽，依此可求长方形的长和宽；还能想到：长方形的宽即圆的直径的长．
【解答】解：圆的直径：2.5×2＝5（厘米）；
长方形的长：2.5×5＝12.5（厘米）；
长方形的宽：2.5×2＝5（厘米）；
还能想到：长方形的宽即圆的直径的长；
答：圆的直径是5厘米，长方形的长是12.5厘米，宽是5厘米；
故答案为：5，12.5，5．
半径/m
0.4
直径/m
8.64
37
2
半径/m
0.4
4.32
18.5
1