浙教版八年级上册2.8 直角三角形全等的判定练习题

这是一份浙教版八年级上册2.8 直角三角形全等的判定练习题，共15页。试卷主要包含了8 直角三角形全都的判定等内容，欢迎下载使用。

一、选择题
1．如图，已知，垂足为，，，则可得到，理由是( )
A．B．C．D．
2．如图，△ABC和△EDF中，∠B＝∠D＝90°，∠A＝∠E，点B，F，C，D在同一条直线上，再增加一个条件，不能判定△ABC≌△EDF的是( )
A．AB＝EDB．AC＝EF
C．AC∥EFD．BF＝DC
3．如图，点P是∠AOB的平分线上的一点，作PD⊥OA，PE⊥OB，垂足分别是D、E．连接DE交OC于点F．则图中共有（ ）个直角
A．4B．6C．8D．10
4．如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角和之间的关系是（ ）
A．B．
C．D．
5．如图，是的平分线上一点，于，于，下列结论中不正确的是（ ）
A．B．
C．D．
6．如图，AB⊥BC于点B，AD⊥DC于点D，若CB＝CD，且∠1＝30°，则∠BAD的度数是( )
A．90°B．60°C．30°D．15°
7．如图，，，垂足分别为E，F，且，，若，则的度数为（ ）
A．B．C．D．
8．如图，中，，，，，，则等于（ ）
A．B．C．D．
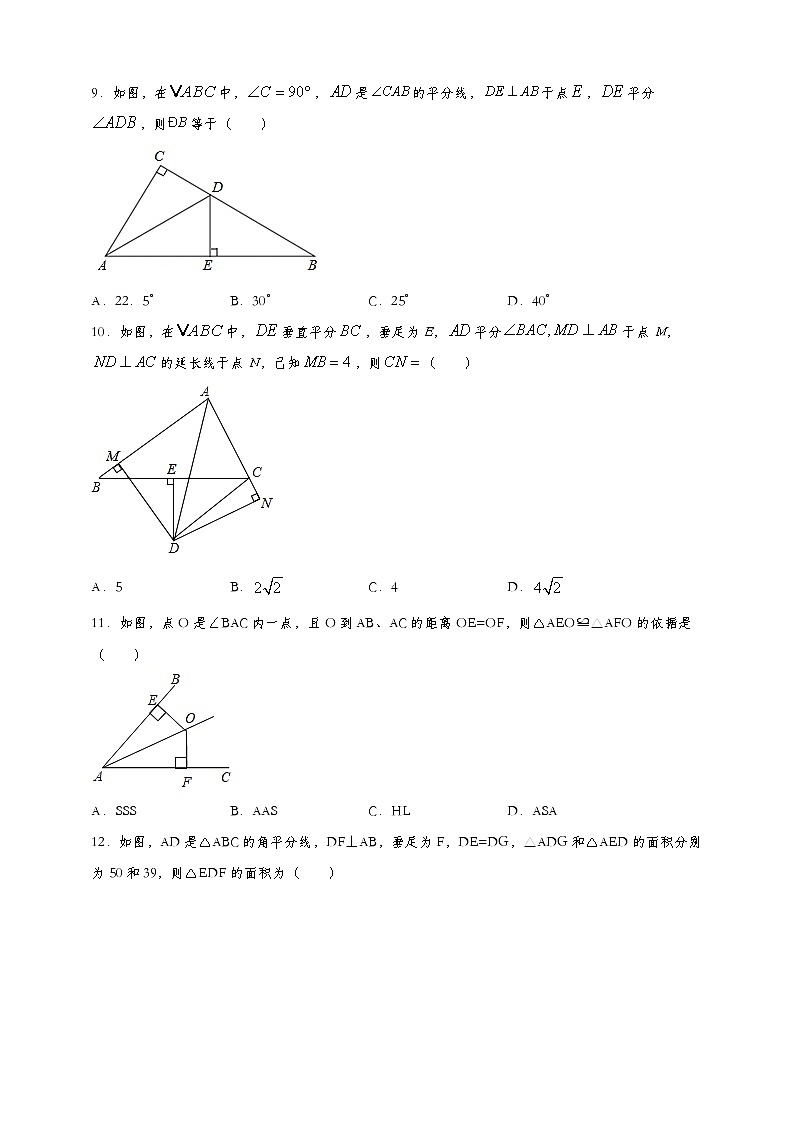
9．如图，在中，，是的平分线，于点，平分，则等于（ ）
A．22．5°B．30°C．25°D．40°
10．如图，在中，垂直平分，垂足为E，平分于点M，的延长线于点N，己知，则（ ）
A．5B．C．4D．
11．如图，点O是∠BAC内一点，且O到AB、AC的距离OE=OF，则△AEO≌△AFO的依据是（ ）
A．SSSB．AASC．HLD．ASA
12．如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（ ）
A．11B．5.5
C．7D．3.5
二、填空题
13．在△ABC中，AB=AC，AD⊥BC，BC=10cm，则CD= ________cm．
14．如图，AC⊥BC，AD⊥BD，垂足分别是C、D，若要用“HL”得到Rt△ABC≌Rt△BAD，则你添加的条件是______________.（写一种即可）
15．如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为48和26，求△EDF的面积_________．
16．如图，在中，，，平分交于点，于点,有下列说法：①；②；③；④若的面积为1，点是边上的中点，则的面积为，其中正确的是______．
17．如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF，则下列结论：①DE＝DF；②AD平分∠BAC；③AE＝AD；④AC﹣AB＝2BE中正确的是_____．
18．如图：有一个直角三角形ABC，∠C＝90°，AC＝10，BC＝5，一条线段PQ＝AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，问P点运动到离A的距离等于___________时，ΔABC和ΔPQA全等．
三、解答题
19．如图，已知，，垂足分别为点、，，平分吗，为什么？
20．已知：如图，△ABC中∠ACB的平分线与AB的垂直平分线交于点D，DE⊥AC于点E，DF⊥BC交CB的延长线于点F．
（1）求证：AE＝BF；
（2）若AC＝24，BC＝10，求AE的长．
21．如图，∠A=∠D=90°，AC=DB，AC、DB相交于点O．求证：OB=OC．
22．如图：AD是的高，E为AC上一点，BE交AD于F，且有BF＝AC，FD＝CD．求证：.
23．如图，点在线段上，，，点在线段上，且满足，连接并延长交于点，连接，．
（1）求证：；
（2）若已知，，，设，则的面积用代数式可表示．你能借助本题提供的图形，证明勾股定理吗？试一试吧！
参考答案
1．A
解:∵
∴∠AOB=∠COD=90°
在Rt△AOB和Rt△COD中
∴（HL）
2．C
A. AB＝ED，可用ASA判定△ABC≌△EDF；
B. AC＝EF，可用AAS判定△ABC≌△EDF；
C. AC∥EF，不能用AAA判定△ABC≌△EDF，故错误；
D. BF＝DC，可用AAS判定△ABC≌△EDF；
3．C
解：∵OP平分∠AOB，PD⊥OA，PE⊥OB，
∴DP=EP，
又∠ODP=∠OEP=90°，OP=OP，
∴Rt△ODP≌Rt△OEP（HL），
∴OD=OE，又DP=EP，
∴OP垂直平分DE，
∴点F处有四个直角，
而点D和点E处分别有两个直角，
∴共有8个直角，
4．D
由题意可知，，，，
与为直角三角形．
在与中，，
，
．
，
．
5．D
∵P是∠ABC的平分线AD上一点，PE⊥AB于E，PF⊥AC于F，
∴PE=PF
故A正确；
在Rt△APE与Rt△APF中，
∵AP=AP，PE=PF，
∴Rt△APE≌Rt△APF（HL）
∴AE=AF
故B、C正确；
无法证明，故D错误.
6．B
解：∵AB⊥BC于B，AD⊥CD于D
∴∠ABC=∠ADC=90°
又∵CB=CD，AC=AC
∴△ABC≌△ADC（HL）
∴∠BAC=∠DAC=30°
∴∠BAD=∠BAC+∠DAC=60°
故选B．
7．C
，
∴，
即．
又，，
和均为直角三角形．
在和中，
，
∴，
．
，
，
．
8．B
，
．
在和中，，
，
．
，
．
9．B
∵在△ABC中，∠C=90°，AD是角平分线，DE⊥AB于E，
∴CD=ED．
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴∠ADC=∠ADE（全等三角形的对应角相等）．
∵∠ADC+∠ADE+∠EDB=180°，DE平分∠ADB，
∴∠ADC=∠ADE=∠EDB=60°．
∴∠B+∠EDB=90°，
∴∠B=30°．
10．D
解：连接BD，如图：
∵DE所在直线是BC的垂直平分线，
∴BD=CD，
∵AD平分∠BAC，DM⊥AB，DN⊥AC，
∴DM=DN，
在Rt△BMD与Rt△CDN中，
∴Rt△BMD≌Rt△CDN（HL），
∴BM=CN=4，
11．C
解：∵OE⊥AB，OF⊥AC，∴∠AEO=∠AFO=90°，
又∵OE=OF，AO为公共边，∴△AEO≌△AFO(HL)
故选C．
12．B
作DM=DE交AC于M，作DN⊥AC，
∵DE=DG，
∴DM=DE，
∵AD是△ABC的角平分线，DF⊥AB，
∴DE=DN，
∴△DEF≌△DNM，
∵△ADG和△AED的面积分别为50和39，
∴S△MDG=S△ADG﹣S△AMG=590﹣39=11，
S△DNM=S△DEF=S△MDG==5.5
13．5
解：∵AD⊥BC，
∴△ADB、△ADC为直角三角形，
在Rt△ADB与Rt△ADC中，
，
∴Rt△ADB≌Rt△ADC（HL），
∴BD=DC=​BC=5cm，
故答案为5．
14．AC=BD或AD=BC.(答案不唯一)
AC=BD或AD=BC都可以.
15．11
解：如图，作DH⊥AC于H，
∵AD是△ABC的角平分线，DF⊥AB，DH⊥AC，
∴DF=DH，
在Rt△FDE和Rt△HDG中，
，
∴Rt△FDE≌Rt△HDG（HL），
同理，Rt△FDA≌Rt△HDA（HL），
设△EDF的面积为x，由题意得，
48﹣x=26+x，
解得x=11，
即△EDF的面积为11，
故答案为：11．
16．①②③
解：∵是等腰直角三角形，
∴，
∵，
∴，
∴是等腰直角三角形，
∴，
∵AD平分，，，
∴，
∴，故①正确；
∵AD平分，
∴，
∵，
∴在中，，故②正确；
在和中，
，
∴，
∴，
∵，
∴，故③正确；
∵是等腰直角三角形，且面积是1，
∴，，
∴，，
∵P是AB中点，
∴，
∴，故④错误．
17．①②④
解：在Rt△BDE和Rt△CDF中，
，
∴Rt△BDE≌Rt△CDF（HL），
∴DE＝DF，故①正确；
又∵DE⊥AB，DF⊥AC，
∴AD平分∠BAC，故②正确；
在Rt△ADE和Rt△ADF中，
，
∴Rt△ADE≌Rt△ADF（HL），
∴AE＝AF，
∴AB+BE＝AC﹣FC，
∴AC﹣AB＝BE+FC＝2BE，
即AC﹣AB＝2BE，故④正确；
由垂线段最短可得AE＜AD，故③错误，
综上所述，正确的是①②④．
18．5或10
∵∠C=90°，AQ⊥AC，
∴∠C=∠QAP=90°，
（1）当AP=BC=5时，
在RtΔACB和RtΔQAP中,
∴RtΔACB≌RtΔQAP(HL)；
（2）当AP=CA=10时，
在RtΔACB和RtΔPAQ中，
∴RtΔACB≌RtΔPAQ(HL)；
故答案为5或10.
19．解：平分．理由：
∵，，
∴与都是直角三角形．
∵，，
∴≌（HL）．
∴．
即平分．
20．解：（1）连接AD
∵∠ACB的平分线与AB的垂直平分线交于点D，DE⊥AC，DF⊥BC
∴DE=DF，DA=DB
∴Rt△ADE≌Rt△BDF
∴AE＝BF；
（2）∵CD平分∠ACB
∴∠ACD=∠BCD
∵DE⊥AC，DF⊥BC
∴∠CED=∠CFD=90°
∴∠CDE=90°－∠ACD=90°－∠BCD=∠CDF
∴CE=CF
∴AC－AE=BC＋BF
∴24－AE=10＋AE
解得：AE=7
21．证明：在Rt△ABC和Rt△DCB中
，
∴Rt△ABC≌Rt△DCB（HL），
∴∠OBC=∠OCB，
∴BO=CO．
22．证明： ∵AD⊥BC，
∴∠BDF＝∠ADC＝90°．
又∵BF＝AC，FD＝CD，
∴△RtADC≌Rt△BDF（HL）．
∴∠EBC＝∠DAC．
又∵∠DAC＋∠ACD＝90°，
∴∠EBC＋∠ACD＝90°．
∴BE⊥AC．
23．（1）因为在和中，
所以，
所以．
因为，，
所以，
所以，
所以．
（2）由题意，得
．
因为，
所以，
所以．