初中数学华师大版九年级上册4. 相似三角形的应用教案配套ppt课件

这是一份初中数学华师大版九年级上册4. 相似三角形的应用教案配套ppt课件，共25页。PPT课件主要包含了课前导学，热身训练，探究与合作，旗杆的高度，例题导析，解存在等内容，欢迎下载使用。

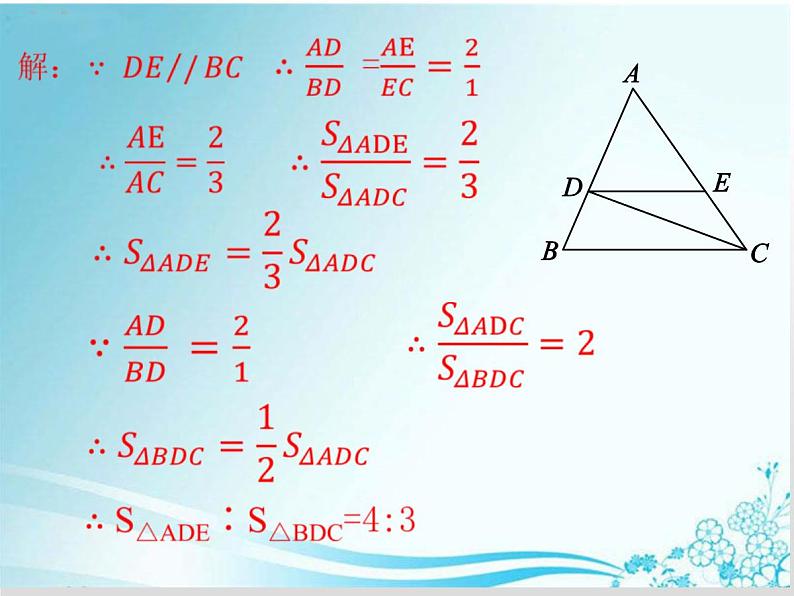
1.如图所示，在△ABC中，DE∥BC交AB于点D，交AC于点E，且AE∶EC＝2∶1，连结DC，求S△ADE∶S△BDC的值．
【自主学习】阅读教材第72-74页，并完成下列各题
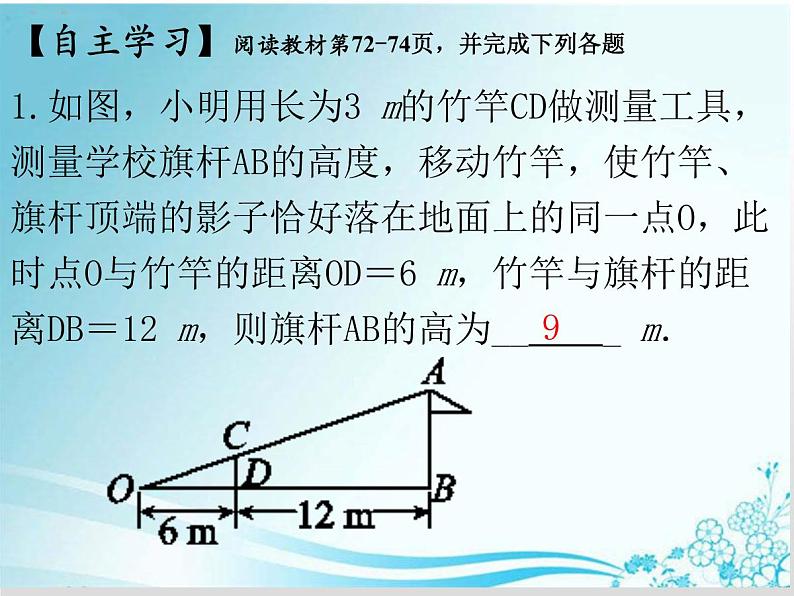
1.如图，小明用长为3 m的竹竿CD做测量工具，测量学校旗杆AB的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面上的同一点O，此时点O与竹竿的距离OD＝6 m，竹竿与旗杆的距离DB＝12 m，则旗杆AB的高为__ _ m．
2. 小明在测量楼高时，先测出楼房落在地面上的影长BA为15米，然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高约为 米。
探究点1：利用阳光下的影子测量旗杆的高度(这是直接运用相似三角形的方法).
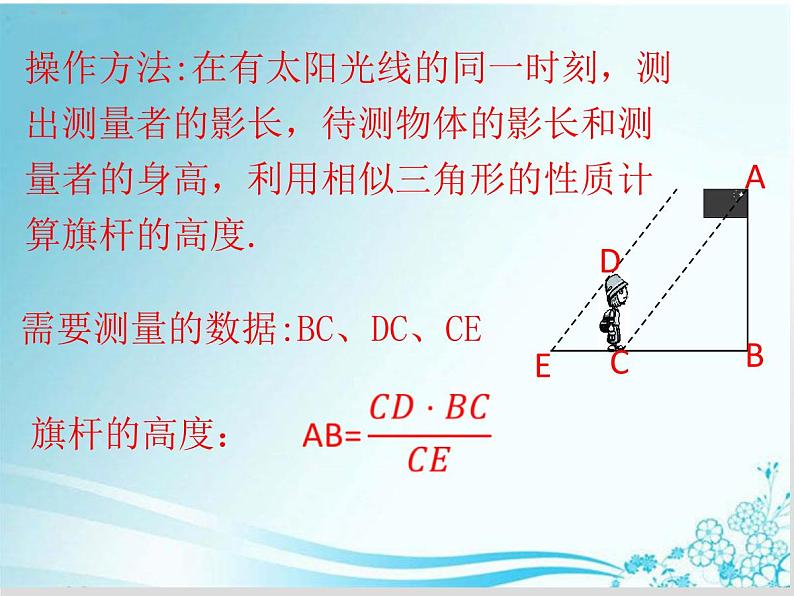
1.根据下图，你能说说具体操作方法吗？2.需要测量哪些数据呢？3.能否用字母表示出测量的数据，并用相应的字母表示出旗杆的高度？
操作方法:在有太阳光线的同一时刻，测出测量者的影长，待测物体的影长和测量者的身高，利用相似三角形的性质计算旗杆的高度.
需要测量的数据:BC、DC、CE
探究点2：利用标杆测量旗杆的高度(这是间接运用相似三角形的方法).
操作方法:用直尺或标杆的长(高)作为三角形的边，利用视点(观察物体时人的眼睛的位置)和盲区(人的视线看不到的区域)构造相似三角形.
需要测量的数据:BC、DE、CE
探究点3：利用平面镜的反射测量旗杆的高度(这是直接运用相似三角形的方法).
操作方法:测出观测者站立点与镜面标记点的距离，待测物体底部与镜面标记点的距离以及观测者眼睛距地面的高度，利用相似三角形的性质计算待测物体的高度.(如图)
1.如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人调整自己的位置，当楼的顶部M、颖颖的头顶B及亮亮的眼睛A恰好在一条直线上时，两人分别标定自己的位置C，D，然后测出两人之间的距离CD＝1.25 m，颖颖与楼之间的距离DN＝30 m，
颖颖的身高BD＝1.6 m，亮亮蹲地观测时眼睛到地面的距离AC＝0.8 m．你能根据以上测量数据帮助他们求出该楼的高度吗？
如图所示,过A作CN的平行线交BD于E,交MN于F.
由题意可得：FN= ED=AC=0.8m , AE=CD=1.25m，EF=DN=30m
2.如图所示，某校计划将一块形状为锐角△ABC的空地进行生态环境改造，已知△ABC的边BC长为120 m，高AD长为80 m，学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分，现计划在△AHG上种草，在△BHE、△GFC上种花. 问：当FG长为多少米时，种草的面积与种花的面积相等？
根据种草面积与种花面积相等，可列方程为：
3. 如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，D，E分别是边AB，AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR∥BA交AC于R，当点Q与点C重合时，点P停止运动．设BQ＝x，QR＝y.
(1)求点D到BC的距离DH的长；
(2)求y关于x的函数关系式(不写自变量的取值范围)；
(3)是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由．
(l)若李华距灯柱OP的水平距离OA=a，求他影子AC的长；
(2)若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值？请说明理由；