初中数学华师大版九年级上册24.4 解直角三角形多媒体教学课件ppt

这是一份初中数学华师大版九年级上册24.4 解直角三角形多媒体教学课件ppt，共16页。PPT课件主要包含了复习回顾，特殊三角角函数值表，自主学习，船有无触礁的危险吗，这个问题归结为，问题情境，探究与合作，解直角三角形，正弦余弦，及时反馈二等内容，欢迎下载使用。

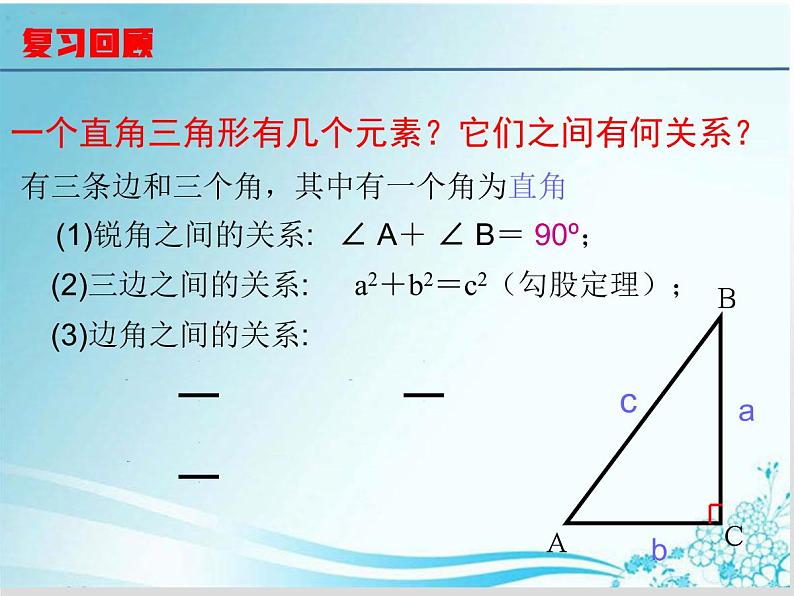
一个直角三角形有几个元素？它们之间有何关系？
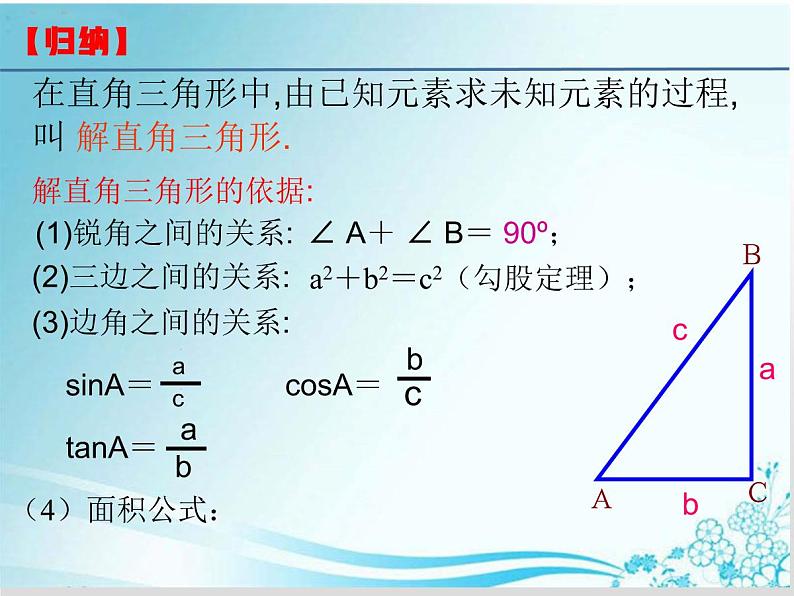
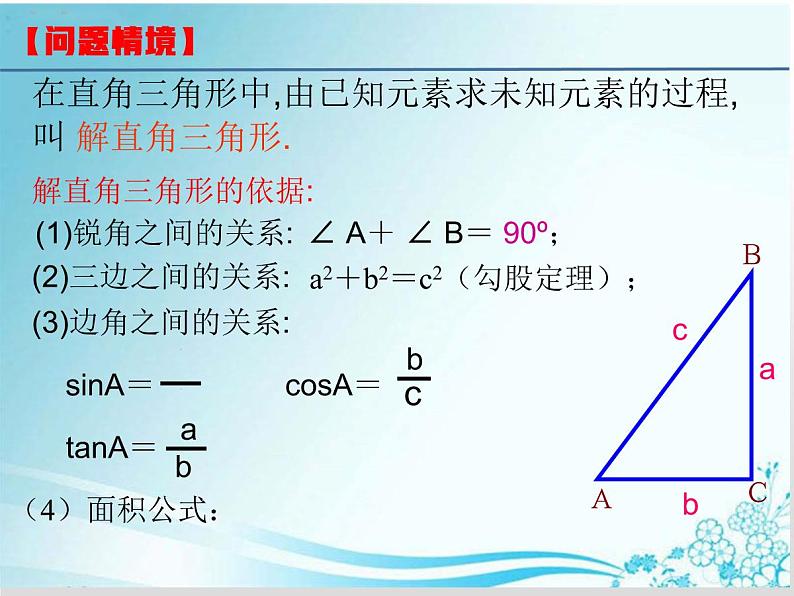
(2)三边之间的关系:
a2＋b2＝c2（勾股定理）；
(1)锐角之间的关系:
∠ A＋ ∠ B＝ 90º；
(3)边角之间的关系:
有三条边和三个角，其中有一个角为直角
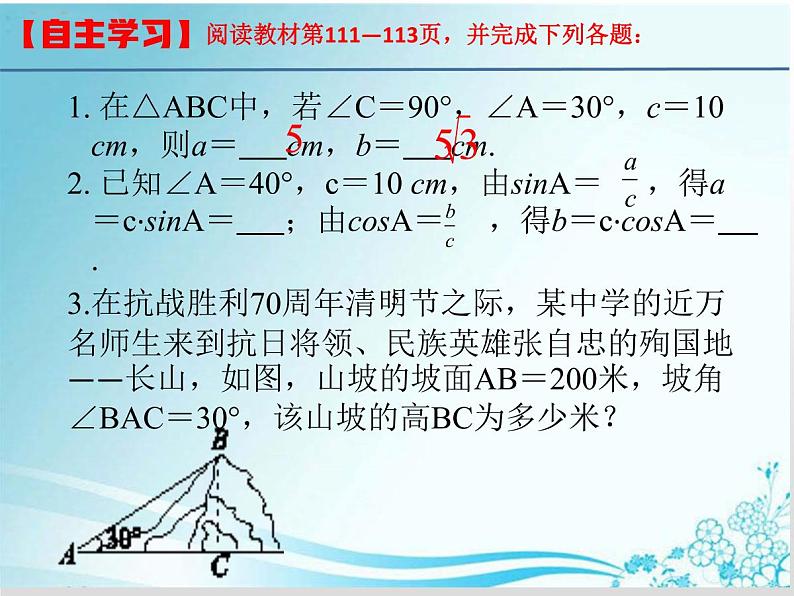
1. 在△ABC中，若∠C＝90°，∠A＝30°，c＝10 cm，则a＝ cm，b＝ cm.2. 已知∠A＝40°，c＝10 cm，由sinA＝ ，得a＝c·sinA＝ ；由csA＝ ，得b＝c·csA＝ .
3.在抗战胜利70周年清明节之际，某中学的近万名师生来到抗日将领、民族英雄张自忠的殉国地——长山，如图，山坡的坡面AB＝200米，坡角∠BAC＝30°，该山坡的高BC为多少米？
阅读教材第111—113页，并完成下列各题：
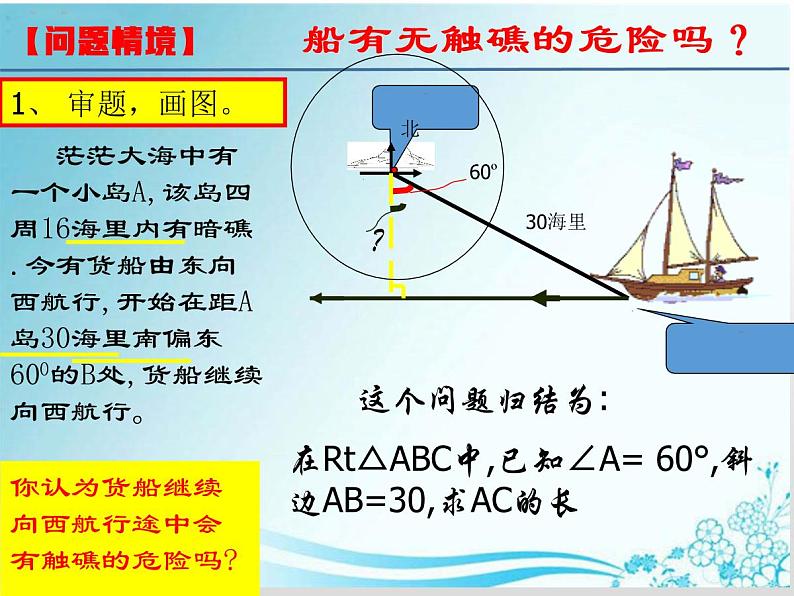
你认为货船继续向西航行途中会有触礁的危险吗?
茫茫大海中有一个小岛A,该岛四周16海里内有暗礁.今有货船由东向西航行,开始在距A岛30海里南偏东600的B处,货船继续向西航行。
在Rt△ABC中,已知∠A= 60°,斜边AB=30,求AC的长
探究点1：解直角三角函数在Rt△ABC中，∠C＝90°，(1)已知BC＝ ，AC＝ ，求其余元素； (2)AB＝30，∠A＝60°，求其余元素；
在直角三角形中，由已知元素求出未知元素的过程，叫做 .通常有 类, 即： 。
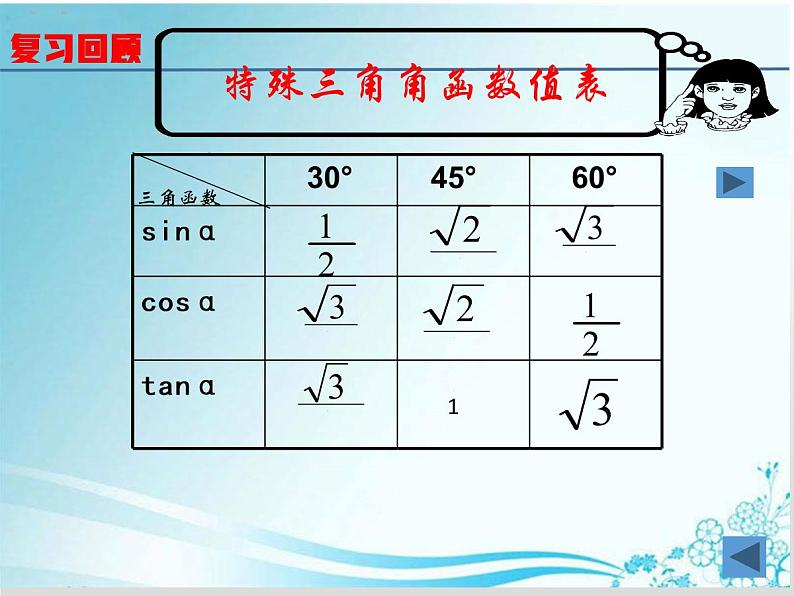
1、已知两直角边，2、已知斜边与一条直角边，3、已知直角边与锐角，4、已知斜边与锐角
在直角三角形中,由已知元素求未知元素的过程,叫
例1.如图所示，一棵大树在一次强烈的地震中于离地面10米处折断倒下，树顶落在离树根24米处.大树在折断之前高多少？
　13＋5＝18（米）.
利用勾股定理可以求出折断倒下部分的长度为:
答:大树在折断之前高为18米.
例2：如图，在相距2000米的东、西两炮台A、B处同时发现入侵敌舰C，在炮台A处测得敌舰C在它的南偏东400的方向，炮台B处测得敌舰C在它的正南方，试求敌舰与两炮台的距离。（精确到1米）
∵∠CAB＝90゜－∠DAC＝50゜，
∴ BC ＝AB•tan∠CAB
=2000×tan50゜
答：敌舰与A、B 两炮台的距离分别约为3111米和2384米.
1．在△ABC中，∠C＝90°，AC＝ ，BC＝ ，解这个直角三角形.
2.在△ABC中，∠C＝90°，AC＝10，∠A＝30°，解这个直角三角形.
探究点2：有“斜”用“弦”，无“斜”用“切”
在Rt△ACB中，∠C＝90°，AB＝10，sinA＝ ，csA＝ ，tanA＝ ，则BC的长为 。 涉“斜”选“弦”的策略：当已知和所求涉及直角三角形的 时，应选择与斜边相关的已知角的 、 ．我们把它叫做涉“斜”( )选“弦”( )的策略.
1.如图，在Rt△ABC中，CA＝CB，AB＝9，点D在BC边上，连结AD，若tan∠CAD＝3(1)，则BD的长为 .
2.如图，在△ABC中，∠C＝45°，点D在AB上，点E在BC上，若AD＝DB＝DE，AE＝1，则AC的长为( ) A.　　　B．2　　C.　　　D.
探究点3：无“斜”选“切”
1如图，在Rt△ABC中，若∠A＝60°，AC＝20 m，则BC的长是 。
2.如图，在△ABC中，∠A＝45°，∠B＝30°，CD⊥AB，垂足为D，若CD＝1，则AB的长为__ .
1.如图，四边形ABCD中，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB＝4，AD＝6，则tanB＝( )　A．2 B．2 C.4(11) D.4(5)
2. 在Rt△ABC中，∠A＝90°，有一个锐角为60°，BC＝6.若点P在直线AC上(不与点A，C重合)，且∠ABP＝30°，则CP的长为__ .