数学七年级上册3.1.1 一元一次方程图片课件ppt

这是一份数学七年级上册3.1.1 一元一次方程图片课件ppt，共19页。PPT课件主要包含了试一试，女儿的问题，你今年几岁了，妈妈的问题，y+434，爸爸的问题，填一填，一星级，二星级，三星级等内容，欢迎下载使用。

知识与技能目标 认识方程的意义；了解方程思想进化过程；认知方程的定义，方程的元，方程的次数，方程的解，一元一次方程的判定。过程与方法目标 通过熟悉算术到方程的演变过程，进而掌握用字母表示数和用字母表示未知数的思想。应用实际问题掌握列方程步骤，列式及寻找等量关系。情感态度价值观 方程的应用是最切合生活现实的，让我们一起领略方程的简便和方程的特殊现实魅力。
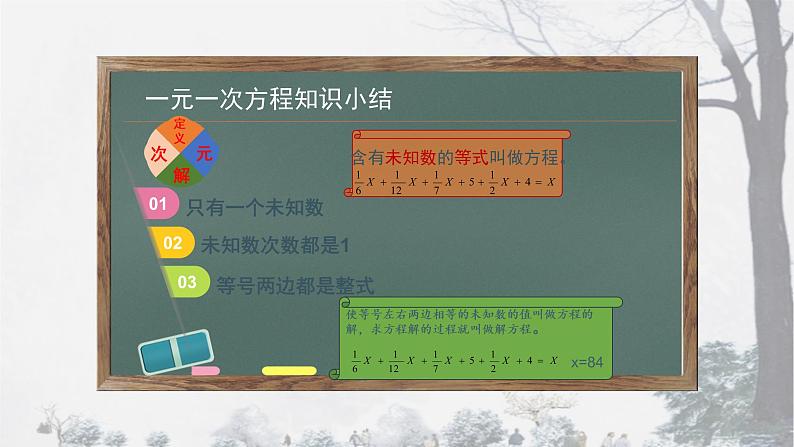
含有未知数的等式叫做方程。
使等号左右两边相等的未知数的值叫做方程的解，求方程解的过程就叫做解方程。
1、y的2倍加上5等于21，可列出方程___________2、y的3倍等于y与7的差，可列出方程____________3、长方形的宽为x，长比宽多3，如果长方形周长为22，则可列出关于x的方程_______________________
2[x+(x+3)]=22
请你根据题意提供的等量关系，列出相应的方程：
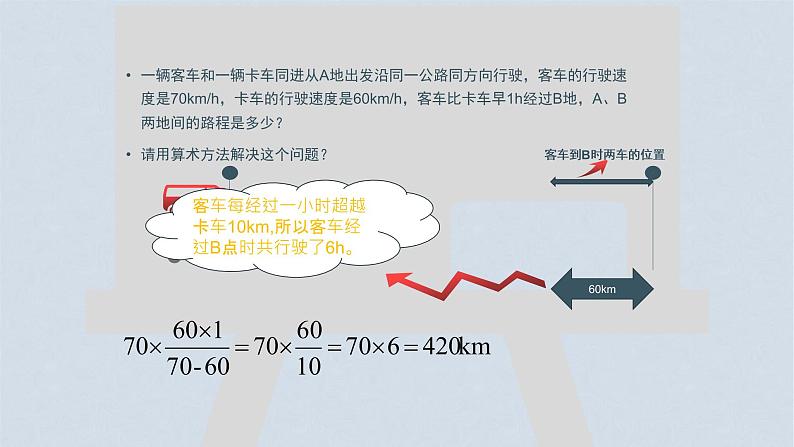
一辆客车和一辆卡车同进从A地出发沿同一公路同方向行驶，客车的行驶速度是70km/h，卡车的行驶速度是60km/h，客车比卡车早1h经过B地，A、B两地间的路程是多少？请用算术方法解决这个问题？
客车每经过一小时超越卡车10km,所以客车经过B点时共行驶了6h。
代数之父─丢番图(Diphantine)是一位古希腊的大数学家，为第一位懂得使用符号代表数来研究问题的人。
坟中安葬着丢番图，多么令人惊讶，它忠实地记录了所经历的道路。
上帝给予的童年占六分之一，
又过十二分之一，两颊长胡，
再过七分之一，点燃起结婚的蜡烛。
可怜迟到的宁馨儿，享年仅及其父之半，便进入冰冷的墓。
悲伤只有用数论的研究去弥补，又过四年，他也走完了人生的旅途。
我班共有40个小朋友，其中男孩子比女孩子多8人，你能说说我班男孩和女孩各有几人么？请列出方程。
如果设男孩为x人，则女孩为(x-8) 人，由题意可得：　　
　　x+(x-8)=40
如果设女孩为x人，则男孩为(x+8)人，由题意可得：
妈妈今年34岁，比女儿琪琪的年龄的5倍还多4岁，你们能猜出琪琪今年几岁吗？
列算式计算：（34－4）÷5
如果设琪琪的年龄为y 岁，由题意可得：
你来猜猜琪琪今年几岁！
银行一年期定期利率为％，去年9月1日爸爸存了一笔钱到银行，今年8月31日到期时取出，本息一共是800元，问爸爸当时存了几元钱？请列出方程。
x％x ＝ 800
如果设去年爸爸存了x元钱，由题意可得：
在一个方程中，只含有一个未知数x（元），并且未知数的指数是1（次），这样的方程叫做一元一次方程。
这些方程有什么共同点？
下列式子是一元一次方程吗？
2、在一卷公元前1600年左右遗留下来的古埃及草卷中，记载着一些数学问题。其中一个问题翻译过来是：“啊哈，它的全部，它的七分之一，其和等于19。”你能求出问题中的“它”吗？
挑战自我：根据题意列方程
1、小颖种了一株树苗，开始时树苗高为40厘米，栽种后每周树苗长高约15厘米，大约几周后树苗长高到1米？
3、甲、乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1分，负一场得0分。甲队与乙队一共比赛了10场，甲队保持了不败记录，一共得了22分，甲队胜了多少场？平了多少场？
含一个未知数，并且未知数的次数是一次，等号两边都是整式。这样的方程叫做一元一次方程。列方程的步骤：1、认真读题，找出其中的数量关系及等量关系2、根据实际问题设未知数3、根据等量关系列方程
谈一谈：本节课你有何收获？
1.课本第80页，习题1-4。2.阅读P84的方程小史。3.实践活动：收集从生活中找得的不同的能用方程解决的例子，并在小组内互相交流。
银行一年期定期利率为％，去年9月1日爸爸存了一笔钱到银行，到今年8月31日到期时取出，本息一共是800元，问爸爸当时存了几元钱？请列出方程。