






2020版高考数学(天津专用)大一轮精准复习课件:7.1 不等式及其解法 【KS5U 高考】
展开(i)传递性:a>b,b>c⇒② a>c .(ii)同向可加性:a>b,c>d⇒a+c>b+d.(iii)关于乘法、乘方、开方的性质:a>b,c>0⇒③ ac>bc ;a>b,c<0⇒④ ac
2.不等式的性质(1)双向性质:a>b⇔b
(i)a>b,ab>0⇒⑧ < ;(ii)a<0
3.不等式的一些常用结论(1)倒数性质:
考向 利用不等式的性质比较实数大小
例 (2014四川文,5,5分)若a>b>0,c
考点二 不等式的解法
考向基础 1.不等式ax>b的解集:若a>0,解集为① ;若a<0,解集为 ;若a=0,当b≥0时,解集为② ⌀ ,当b<0时,解集为R.
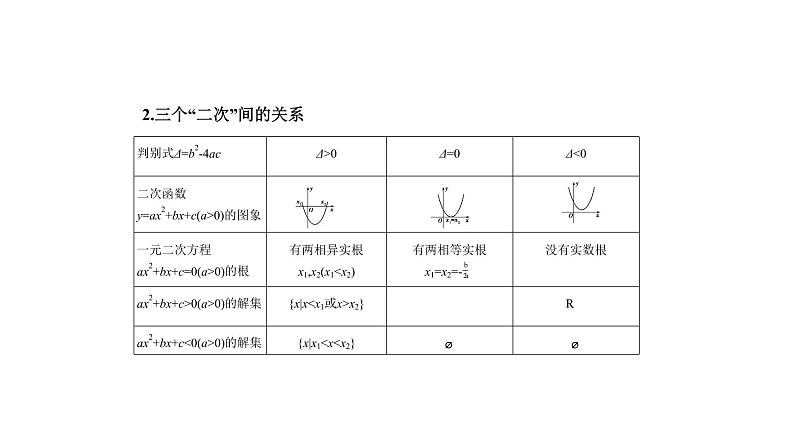
2.三个“二次”间的关系
3.一元n次不等式的求解方法如果一元n次不等式a0xn+a1xn-1+…+an>0(a0≠0,n∈N*,n≥3)可以转化为a0 (x-x1)(x-x2)…(x-xn)>0(其中x1
(1)|f(x)|>|g(x)|⇔④ [f(x)]2>[g(x)]2 ;(2)|f(x)|>g(x)⇔⑤ f(x)>g(x)或f(x)<-g(x) ;(3)|f(x)|
考向 求不等式组的解集
例 (2014大纲全国文,3,5分)不等式组 的解集为 ( )A.{x|-2
解析 由x(x+2)>0得x>0或x<-2;由|x|<1得-1
例1 已知x,y∈R,那么“x>y”的充分必要条件是 ( )A.2x>2y B.lg x>lg yC. > D.x2>y2
解析 由x,y∈R,排除B和C.对于A,由于函数y=2x在R上为增函数,当x>y时,可得2x>2y.反之也成立.对于D,y=x2在R上不单调,故不符合题意.故选A.
方法2 比较实数大小的常用方法实数大小的比较常用“比较法”来解决,“比较法”有“作差比较法” 和“作商比较法”两种,可根据数式的结构特点灵活选用.比较法的关 键是变形,变形越彻底,越有利于下一步的判断.在用“比较法”时,有时 可先将原式变形后再作差或作商进行比较,若是选择题,还可用特殊值 法判断数的大小关系.(1)作差法理论依据:a-b>0⇔a>b;a-b<0⇔a
例2 若0
解析 解法一:作差法.∵0
∵0
方法3 一元二次不等式恒成立问题的解法1.解决恒成立问题可以利用分离参数法,一定要弄清楚谁是自变量,谁是 参数.一般地,知道谁的范围,谁就是自变量,求谁的范围,谁就是参数.2.对于一元二次不等式恒成立问题,恒大于0就是相应的二次函数的图 象在给定的区间上全部在x轴上方,恒小于0就是相应的二次函数的图象 在给定的区间上全部在x轴下方.3.解决不等式在给定区间上的恒成立问题,可先求出相应函数这个区间 上的最值,再转化为与最值有关的不等式问题.
例3 (1)不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则实数a的取值 范围是 .(2)(2014江苏,10,5分)已知函数f(x)=x2+mx-1,若对于任意x∈[m,m+1],都 有f(x)<0成立,则实数m的取值范围是 .
2020版高考数学(天津专用)大一轮精准复习课件:9.4 双曲线及其性质 【KS5U 高考】: 这是一份2020版高考数学(天津专用)大一轮精准复习课件:9.4 双曲线及其性质 【KS5U 高考】,共13页。
2020版高考数学(天津专用)大一轮精准复习课件:7.2 基本不等式 【KS5U 高考】: 这是一份2020版高考数学(天津专用)大一轮精准复习课件:7.2 基本不等式 【KS5U 高考】,共10页。
2020版高考数学(天津专用)大一轮精准复习课件:6.1 数列的概念及其表示 【KS5U 高考】: 这是一份2020版高考数学(天津专用)大一轮精准复习课件:6.1 数列的概念及其表示 【KS5U 高考】,共14页。












