数学苏科版2.4 圆周角课前预习ppt课件

这是一份数学苏科版2.4 圆周角课前预习ppt课件，共13页。PPT课件主要包含了学习目标，新课导入，新课讲解，解∠1∠2，知识点，若AC是直径，课堂小结，圆周角定理的推论，当堂小练，等边三角形等内容，欢迎下载使用。

理解掌握圆周角定理的推论及其证明过程和运用. （难点）
2.圆周角定理 一条弧所对的圆周角等于它所对的圆心角的一半.
1.圆周角定义： 顶点在圆上，并且两边都与圆相交的角叫做圆周角.
根据圆周角定理我们可以得到哪些推论呢？
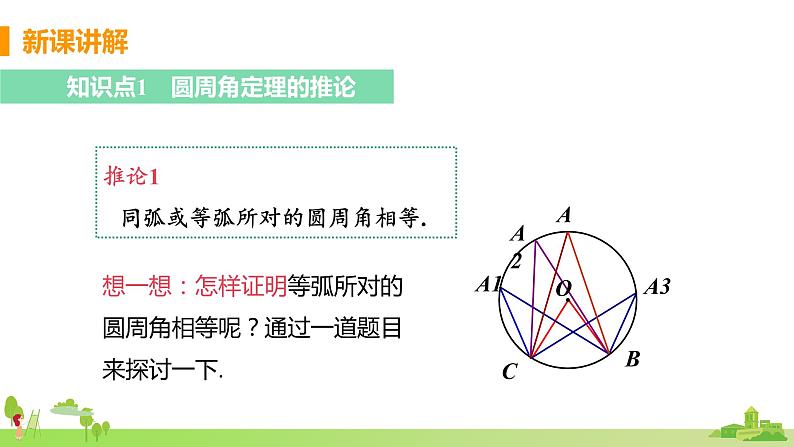
知识点1 圆周角定理的推论
推论1 同弧或等弧所对的圆周角相等.
想一想：怎样证明等弧所对的圆周角相等呢？通过一道题目来探讨一下.
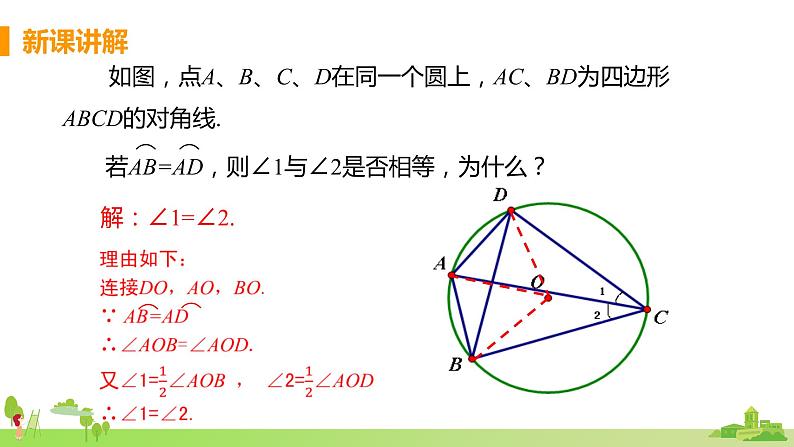
如图，点A、B、C、D在同一个圆上，AC、BD为四边形ABCD的对角线.
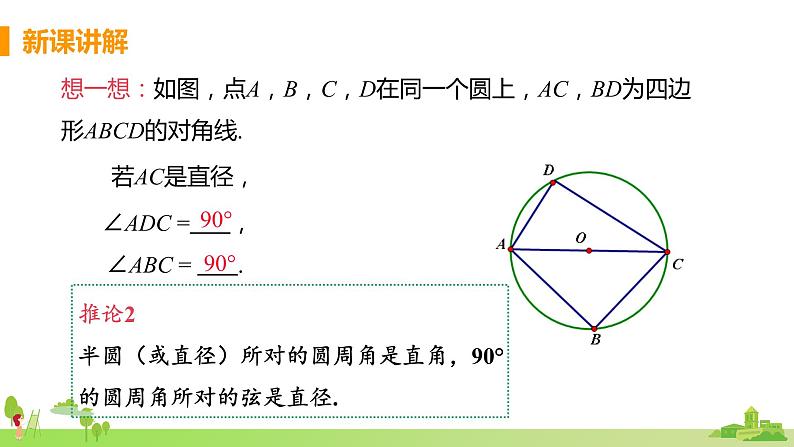
推论2半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.
想一想：如图，点A，B，C，D在同一个圆上，AC，BD为四边形ABCD的对角线.
若AC是半圆， ∠ADC = ，∠ABC = .
1 如图，⊙O的直径AC为10cm，弦AD为6cm.（1）求DC的长；
（2）若∠ADC的平分线交⊙O于B, 求AB、BC的长．
在Rt△ABC中，AB2+BC2=AC2，
(2)∵ AC是直径,∴ ∠ABC=90°. ∵BD平分∠ADC,∴∠ADB=∠CDB. 又∵∠ACB=∠ADB ,∠BAC=∠BDC . ∴ ∠BAC=∠ACB, ∴AB=BC.
90°的圆周角所对的弦是直径.
1．如图，AB是⊙O的直径，∠A＝10°，则∠ABC=________．
2．如图，AB是⊙O的直径，D是⊙O上的任意一点（不与点A、B重合），延长BD到点C，使DC＝BD，判断△ABC的形状： ．
如图，BC为半圆O的直径，点F是BC上一动点(点F不与B、C重合)，A是BF上的中点，设∠FBC=α，∠ACB=β．(1)当α=50°时，求β的度数;(2)猜想α与β之间的关系，并给予证明.