






高中3.1弧度制与任意角教学演示ppt课件
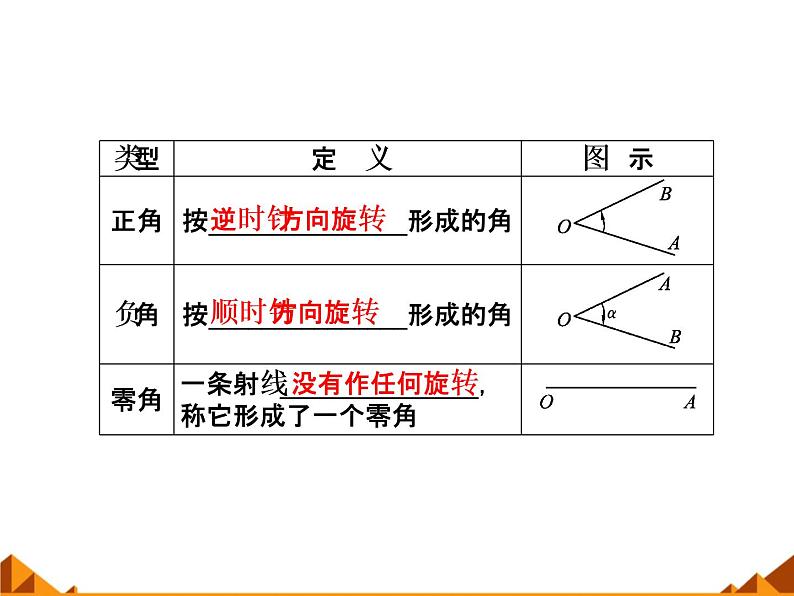
展开角的概念(1)角的概念:角可以看成平面内_________绕着_____从一个位置____到另一个位置所形成的图形.(2)角的分类:按旋转方向可将角分为如下三类:
象限角角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合,那么,角的终边落在第几象限,就说这个角是__________.如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=_________,k∈Z},即任一与角α终边相同的角,都可以表示成角α与___________的和.
若α是第四象限的角,那么 是第二象限的角吗?如果不是,请说明理由.
5分钟的时间,分针所转过的角度是 ( ).A.360° B.-360°C.5° D.-30°答案 D下列各角中是第二象限角的有________个 ( ).①125° ②195° ③-200° ④179°A.1 B.2 C.3 D.4解析 ①、③、④中的角都是第二象限角,故选C.答案 C
与25°角终边相同的角的集合是 ( ).A.{α|α=25°+360°}B.{α|α=25°+k·180°,k∈Z}C.{α|α=25°+k·360°,k∈Z}D.{α|α=-25°+k·360°,k∈Z}答案 C在0°~360°范围的与-30°终边相同的角是________.答案 330°
对象限角的认识(1)象限角的前提条件是:角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合.(2)角的终边在第几象限,就说这个角是第几象限的角(或者说这个角属于第几象限).各象限角的集合表示如下:第一象限角:{α|k·360°<α<k·360°+90°,k∈Z};第二象限角:
{α|k·360°+90°<α<k·360°+180°,k∈Z};第三象限角:{α|k·360°+180°<α<k·360°+270°,k∈Z};第四象限角:{α|k·360°+270°<α<k·360°+360°,k∈Z}.(3)角的终边若落在坐标轴上,就说这个角不属于任何象限,称它为轴线角(或称为象限界角).轴线角的集合表示如下:
{α|α=k·360°,k∈Z} {α|α=180°+k·360°,k∈Z}
{α|α=90°+k·360°,k∈Z} {α|α=270°+k·360°,k∈Z}对终边相同的角的认识(1)研究终边相同的角的前提条件是:角的顶点在坐标原点,角的始边与x轴的非负半轴重合.
(2)对于与角α终边相同的角的集合S={β|β=α+k·360°,k∈Z}明确以下几点:k为整数;α为任意角;k·360°与α之间用“+”号连接,如k·360°-30°应看成是k·360°+(-30°);终边相同的角不一定相等,但相等的角终边一定相同;终边相同的角有无数多个,它们相差360°的整数倍.
已知角的顶点与坐标原点重合,始边与x轴的非负半轴重合,作出下列各角,并指出它们是哪个象限的角.(1)420° (2)-75° (3)855° (4)-510°解 作出各角的终边如图所示:
题型一 终边相同的角与象限角
由图可知(1)420°是第一象限角;(2)-75°是第四象限角;(3)855°是第二象限角;(4)-510°是第三象限角.
点评 象限角的判定其实有两种方法:一是图象观察法(如上),二是转化为与0°~360°角终边相同的角(今后常用).
在与1 089°角终边相同的角中,求满足下列条件的角.(1)在-360°~720°内;(2)最大的负角;(3)最小的正角.解 与1 089°角终边相同角的一般形式为α=k·360°+1 089°(k∈Z).(1)由-360°≤α<720°,得-360°≤k·360°+1 089°<720°(k∈Z),-1 449°≤k·360°<-369°(k∈Z),所以k=-4,-3,-2,所以在-360°~720°内与角1 089°终边相同的角分别为-351°、9°、369°.(2)由α<0°,得k·360°+1 089°<0°(k∈Z),
(3)由α>0°,得k·360°+1 089°>0°(k∈Z),
写出终边在直线y=x上的角的集合.解 终边在直线y=x上的第一象限角的集合为M={α|α=k·360°+45°,k∈Z},第三象限角的集合为N={α|α=k·360°+225°,k∈Z}.∴终边在直线y=x上的角的集合为M∪N={α|α=k·360°+45°,k∈Z}∪{α|α=k·360°+225°,k∈Z}={α|α=2k·180°+45°,k∈Z}∪{α|α=(2k+1)·180°+45°,k∈Z}={α|α=n·180°+45°,n∈Z}.∴终边在直线y=x上的角的集合为{α|α=n·180°+45°,n∈Z}.
题型二 终边在一条直线上的角
写出终边落在第二、四象限角平分线上的角的集合.解 第二象限时,α=k·360°+135°,k∈Z;第四象限时,α=k·360°+315°=k·360°+180°+135°,即第二象限角α=k·360°+135°=2k·180°+135°,第四象限角α=(2k+1)·180°+135°,k∈Z,综合知:终边在第二、四象限角平分线的角的集合{α|α=k·180°+135°,k∈Z}.
已知α是第二象限角,试确定2α, 的终边所在的位置.解 因为α是第二象限角,所以k·360°+90°<α<k·360°+180°,k∈Z.所以2k·360°+180°<2α<2k·360°+360°,k∈Z,所以2α的终边在第三或第四象限或终边在y轴的非正半轴上.因为k·360°+90°<α<k·360°+180°,k∈Z,
题型三 相关角所在象限的判定
已知α是第三象限角,则 是 ( ).A.第一象限角 B.第二象限角C.第四象限角 D.第二或第四象限角
若α是第三象限的角,则 是 ( ).A.第一象限的角B.第三象限的角C.第四象限的角D.第一象限或第三象限或第四象限的角
误区警示 以偏概全而出错
任意角包括正角、负角、零角.在平面直角坐标系中,当角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合时,角的终边在第几象限就叫做第几象限角,当角的终边在坐标轴上时叫做轴线角(或象限界角).与α终边相同的角有无数多个,这无数多个组成的集合为{β|β=α+k·360°,k∈Z}.
由α所在象限,确定 所在象限,也可用如下方法判断:(1)画出区域:将坐标系每个象限二等分,得8个区域;
(2)标号:自x轴正向逆时针方向把每个区域依次标上Ⅰ,Ⅱ,Ⅲ,Ⅳ(如图所示);(3)确定区域:找出与角α所在象限标号一致的区域,即为所求.
由α所在象限,确定 所在象限,也可用如下方法判断:
高中数学湘教版(2019)必修 第一册第5章 三角函数5.1 任意角与弧度制评优课课件ppt: 这是一份高中数学湘教版(2019)必修 第一册第5章 三角函数5.1 任意角与弧度制评优课课件ppt,文件包含511角的概念的推广doc、511角的概念的推广pptx等2份课件配套教学资源,其中PPT共0页, 欢迎下载使用。
高中3.1弧度制与任意角教课内容ppt课件: 这是一份高中3.1弧度制与任意角教课内容ppt课件,共24页。PPT课件主要包含了自学导引,终边的旋转方向,自主探究,预习测评,答案A,名师点睛,典例剖析等内容,欢迎下载使用。
数学湘教版4.3向量与实数相乘备课课件ppt: 这是一份数学湘教版4.3向量与实数相乘备课课件ppt,共27页。PPT课件主要包含了自学导引,相同或相反,任意的,自主探究,预习测评,名师点睛,题型一向量的运算,典例剖析,题型三共线问题等内容,欢迎下载使用。













