数学八年级上册第十二章 全等三角形12.2 三角形全等的判定教学演示ppt课件

这是一份数学八年级上册第十二章 全等三角形12.2 三角形全等的判定教学演示ppt课件，共29页。PPT课件主要包含了“两角及夹边”，“角边角”判定方法，几何语言，∴ADAE，BECD，∴∠C＝∠F，ACBC，∴ABAD等内容，欢迎下载使用。
一张教学用的三角形硬纸板不小心被撕坏了，如图，你能制作一张与原来同样大小的新教具？能恢复三角形的原貌吗？
怎么办？可以帮帮我吗？
1. 探索并正确理解三角形全等的判定方法“ASA”和“AAS”．
2. 会用三角形全等的判定方法“ASA”和“AAS”证明两个三角形全等．
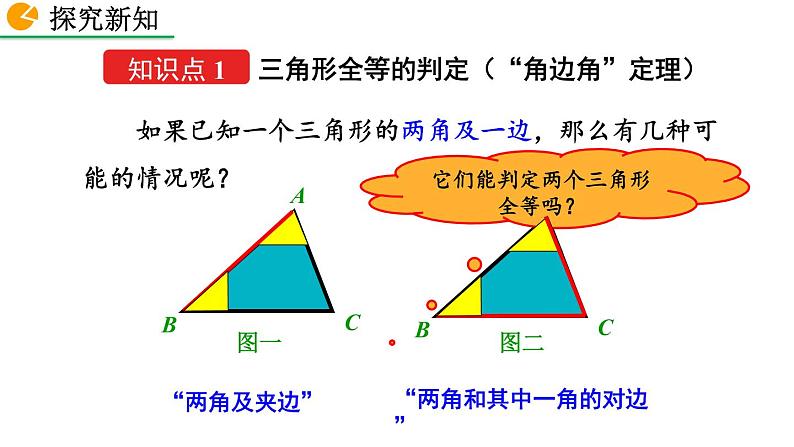
如果已知一个三角形的两角及一边，那么有几种可能的情况呢？
“两角和其中一角的对边”
它们能判定两个三角形全等吗？
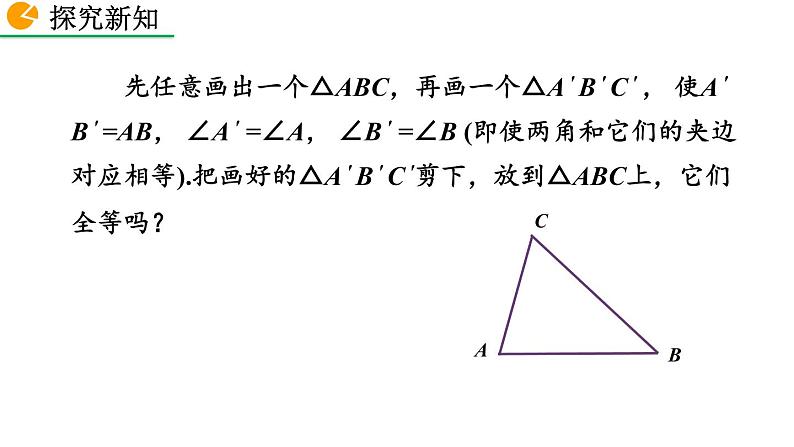
先任意画出一个△ABC，再画一个△A ′ B ′ C ′ ， 使A ′ B ′ =AB， ∠A ′ =∠A， ∠B ′ =∠B (即使两角和它们的夹边对应相等).把画好的△A ′ B ′ C ′剪下，放到△ABC上，它们全等吗？
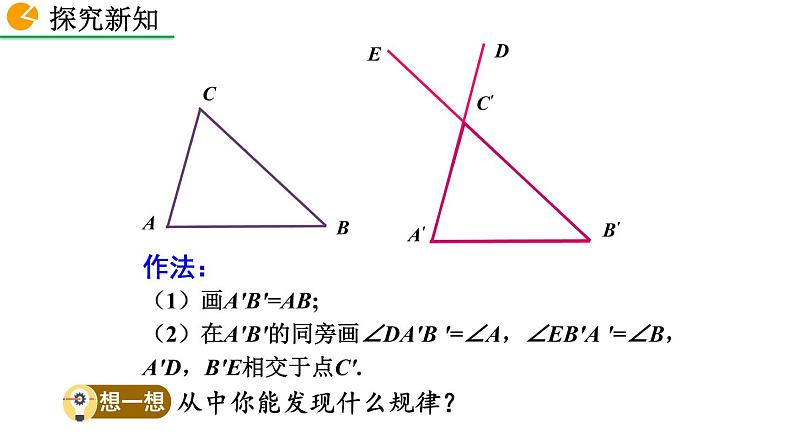
作法：（1）画A'B'=AB;（2）在A'B'的同旁画∠DA'B '=∠A，∠EB'A '=∠B，A'D，B'E相交于点C'.
从中你能发现什么规律？
文字语言： 有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”）.
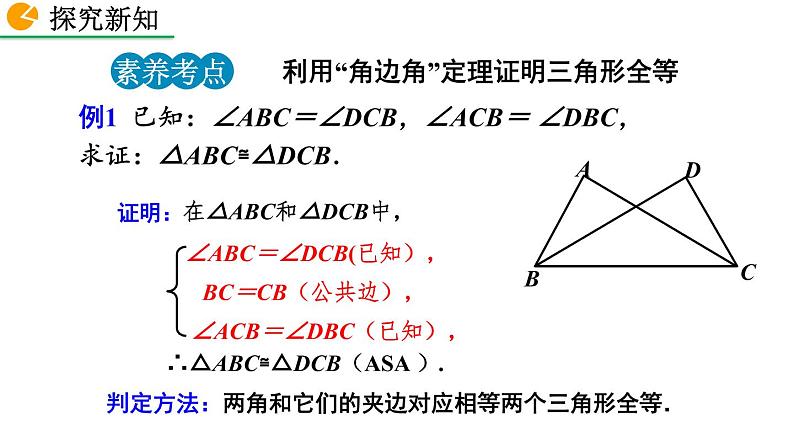
例1 已知：∠ABC＝∠DCB，∠ACB＝ ∠DBC，求证：△ABC≌△DCB．
∠ABC＝∠DCB(已知）， BC＝CB（公共边）， ∠ACB＝∠DBC（已知），
在△ABC和△DCB中，
∴△ABC≌△DCB（ASA ）.
判定方法：两角和它们的夹边对应相等两个三角形全等．
如图，已知点E，C在线段BF上，BE＝CF，AB∥DE，∠ACB＝∠F.求证：△ABC≌△DEF.
证明：∵AB∥DE，∴∠B＝∠DEF，∵BE＝CF，∴BC＝EF.∵∠ACB＝∠F，∴△ABC≌△DEF.（ASA）
例2 如图，点D在AB上，点E在AC上，AB=AC, ∠B=∠C,求证：AD=AE.
分析：证明△ACD≌△ABE，就可以得出AD=AE.
证明：在△ACD和△ABE中，
∠A=∠A（公共角 ）， AC=AB（已知），∠C=∠B （已知 ），
∴ △ACD≌△ABE（ASA），
如图，AD=AE,∠B=∠C，那么BE和CD相等么？为什么？
证明:在△ABE与△ACD中 ∠B=∠C, （已知） ∠A= ∠A, （公共角） AE=AD, （已知）∴ △ABE ≌△ACD.（AAS）∴ BE=CD .（全等三角形对应边相等）
若三角形的两个内角分别是60°和45°，且45°所对的边为3cm，你能画出这个三角形吗?
这里的条件与探究1中的条件有什么相同点与不同点？你能将它转化为探究1中的条件吗？
两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.
例1 在△ABC和△DEF中，∠A＝∠D，∠B＝ ∠E，BC=EF. 求证：△ABC≌△DEF．
在△ABC中，∠A+∠B+∠C＝180°.
∴△ABC≌△DEF（ASA ）.
∠B＝∠E， BC＝EF， ∠C＝∠F.
∴ ∠C＝180°－∠A－∠B.
同理 ∠F＝180°－∠D－∠E.
又 ∠A＝∠D，∠B＝ ∠E,
在△ABC和△DEF中，
例2 如图，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E. 求证：(1)△BDA≌△AEC；
证明：(1)∵BD⊥m，CE⊥m，∴∠ADB＝∠CEA＝90°，∴∠ABD＋∠BAD＝90°.∵AB⊥AC，∴∠BAD＋∠CAE＝90°，∠ABD＝∠CAE.在△BDA和△AEC中，
∠ADB=∠CEA=90°， ∠ABD＝∠CAE,AB＝AC,
∴△BDA≌△AEC(AAS).
例3 如图，已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E. 求证：(2)DE＝BD＋CE.
∴BD＝AE，AD＝CE，∴DE＝DA＋AE＝BD＋CE.
证明：∵△BDA≌△AEC,
方法总结：利用全等三角形可以解决线段之间的关系，比如线段的相等关系、和差关系等，解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化．
如图，已知：AD为△ABC的中线，且CF⊥AD于点F，BE⊥AD交AD的延长线于点E.求证：BE＝CF.
证明：∵AD为△ABC的中线，∴BD＝CD. ∵BE⊥AD，CF⊥AD，∴∠BED＝∠CFD＝90°.在△BED与△CFD中
∠BED=∠CFD,∠1=∠2,BD=CD,
∴△BED≌△CFD(AAS)．∴BE＝CF.
解析：∵AB=AC，∠A为公共角，如添加∠B=∠C，利用ASA即可证明△ABE≌△ACD；如添AD=AE，利用SAS即可证明△ABE≌△ACD；如添BD=CE，等量关系可得AD=AE，利用SAS即可证明△ABE≌△ACD；如添BE=CD，因为SSA，不能证明△ABE≌△ACD，
1.如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（　　）A．∠B=∠C B．AD=AEC．BD=CED．BE=CD
2.如图，已知∠1=∠2，∠B=∠D，求证：CB=CD．
1. 下列各图中a,b,c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是（　　）A．甲和乙 B．乙和丙 C．甲和丙 D．只有丙
2. 在△ABC与△A′B′C′中，已知∠A＝44°，∠B＝67°，∠C′＝69° ，∠A′＝44°，且AC＝A′C′，那么这两个三角形（　 ）A．一定不全等　 B．一定全等　 　C．不一定全等　　 D．以上都不对
3. 如图，已知∠ACB=∠DBC，∠ABC=∠CDB，判别下面的两个三角形是否全等，并说明理由.
不全等，因为BC虽然是公共边，但不是对应边.
4.如图，△ABC的两条高AD，BE相交于点F，请添加一个条件，使得ADC≌△BEC（不添加其他字母及辅助线），你添加的条件是___________.　
1.已知：如图， AB⊥BC，AD⊥DC，∠1=∠2, 求证：AB=AD.
证明： ∵ AB⊥BC，AD⊥DC，
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中，
∴ △ABC≌△ADC (AAS)，
2. 如图,小明不慎将一块三角形模具打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗? 如果可以,带哪块去合适?你能说明其中理由吗?
答：带1去，因为有两角且夹边相等的两个三角形全等.
已知：如图，△ABC ≌△A′B′C′ ，AD，A′ D′ 分别是△ABC 和△A′B′C′的高.试说明AD＝ A′D′ ，并用一句话说出你的发现.
解：因为△ABC ≌△A′B′C′ ，所以AB=A'B'（全等三角形对应边相等），∠ABD=∠A'B'D'（全等三角形对应角相等）.因为AD⊥BC，A'D'⊥B'C'，所以∠ADB=∠A'D'B'.在△ABD和△A'B'D'中，∠ADB=∠A'D'B'（已证），∠ABD=∠A'B'D'（已证），AB=AB（已证），所以△ABD≌△A'B'D'.所以AD=A'D'.
全等三角形对应边上的高也相等.