
湘教版 八年级数学下学期期末模拟卷2(含解析)
展开期末模拟卷(2)
一、选择题(共8小题,每小题4分,满分32分)
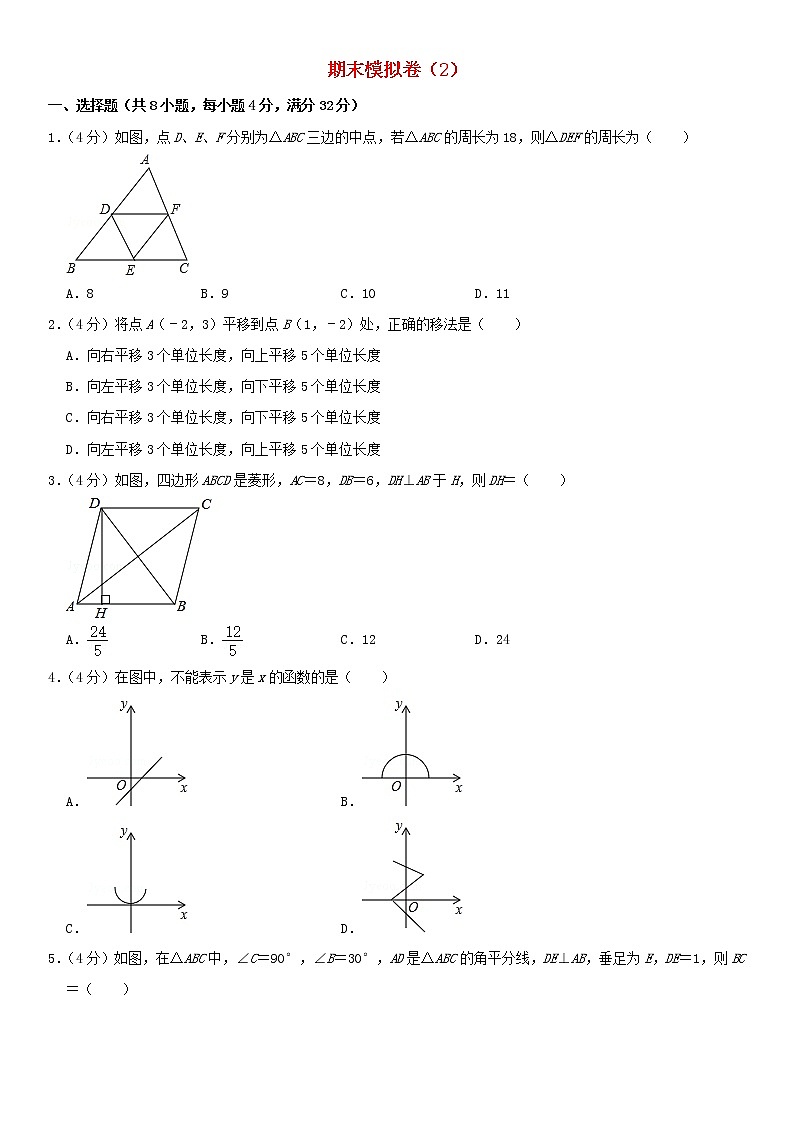
1.(4分)如图,点D、E、F分别为△ABC三边的中点,若△ABC的周长为18,则△DEF的周长为( )
A.8 B.9 C.10 D.11
2.(4分)将点A(﹣2,3)平移到点B(1,﹣2)处,正确的移法是( )
A.向右平移3个单位长度,向上平移5个单位长度
B.向左平移3个单位长度,向下平移5个单位长度
C.向右平移3个单位长度,向下平移5个单位长度
D.向左平移3个单位长度,向上平移5个单位长度
3.(4分)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
A. B. C.12 D.24
4.(4分)在图中,不能表示y是x的函数的是( )
A. B.
C. D.
5.(4分)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B.2 C.3 D.+2
6.(4分)若实数a、b满足ab<0,则一次函数y=ax+b的图象可能是( )
A. B.
C. D.
7.(4分)大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90~110这一组的频率是( )
A.0.1 B.0.2 C.0.3 D.0.7
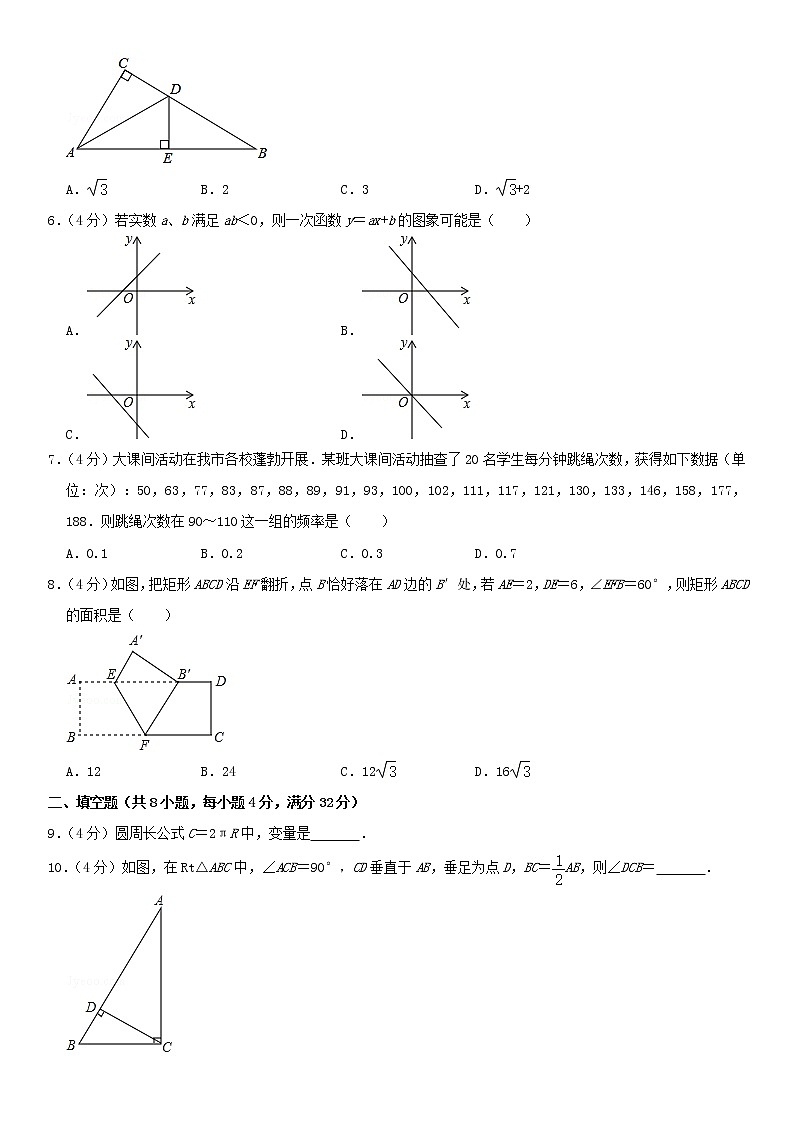
8.(4分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12 B.24 C.12 D.16
二、填空题(共8小题,每小题4分,满分32分)
9.(4分)圆周长公式C=2πR中,变量是 .
10.(4分)如图,在Rt△ABC中,∠ACB=90°,CD垂直于AB,垂足为点D,BC=AB,则∠DCB= .
11.(4分)一个多边形的内角和等于1080°,它是 边形.
12.(4分)如图,∠B=∠ACD=90°,BC=3,AB=4,CD=12,则AD= .
13.(4分)在平面直角坐标系中,已知点P在第二象限,距离x轴3个单位长度,距离y轴2个单位长度,则点P的坐标为 .
14.(4分)下列函数中:①y=﹣x;②y=;③y=﹣x2;④y=﹣x+3;⑤2x﹣3y=1.其中y是x的一次函数的是 (填所有正确答案的序号).
15.(4分)如图,在平行四边形ABCD中,BE平分∠ABC,交AD于点E,AB=3cm,ED=cm,则平行四边形ABCD的周长是 .
16.(4分)弹簧挂上物体后会伸长,测得﹣弹簧的长度y(cm)与所挂重物的质量x(㎏)有下面的关系:那么弹簧总长y(cm)与所挂重物x(㎏)之间的函数关系式为 .
三、解答题(共7小题,满分56分)
17.(7分)如图,平行四边形ABCD的对角线AC=6cm,将平行四边形ABCD绕其对称中心旋转180°,求C点所转过的路径长.
18.(7分)如图,将△ABC先向上平移4个单位,再向左平移5个单位,它的像是△A′B′C′,写出△A′B′C′的顶点坐标,并作出该图形.
19.(8分)如图,△ABC中,∠ACB=90°,D、E分别是BC、BA的中点,连接DE,F在DE延长线上,且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
20.(8分)在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间.
21.(8分)如图,某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,且距A点18海里,航行半小时后到达B点,此时测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
(1)问B点是否在暗礁区域外?
(2)若继续向正东航行,有无触礁危险?请说明理由.
22.(8分)2011年我市体卫站对某校九年级学生体育测试情况进行调研,从该校360名九年级学生中抽取了部分学生的成绩(成绩分为A、B、C三个层次)进行分析,绘制了频数分布表与频数分布直方图(如图),请根据图表信息解答下列问题:
分组 | 频数 | 频率 |
C | 10 | 0.10 |
B |
| 0.50 |
A | 40 |
|
合计 |
| 1.00 |
(1)补全频数分布表与频数分布直方图;
(2)如果成绩为A等级的同学属于优秀,请你估计该校九年级约有多少人达到优秀水平?
23.(10分)在开展“美丽广西,清洁乡村”的活动中某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元.
(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,请你写出y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)如果购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵数不少于A种树苗棵数的3倍,那么有哪几种购买树苗的方案?
(3)从节约开支的角度考虑,你认为采用哪种方案更合算?
期末模拟卷(2)
参考答案与试题解析
一、选择题(共8小题,每小题4分,满分32分)
1.(4分)如图,点D、E、F分别为△ABC三边的中点,若△ABC的周长为18,则△DEF的周长为( )
A.8 B.9 C.10 D.11
【解答】解:
∵D、E、F分别是AB、BC、AC的中点,
∴ED、FE、DF为△ABC中位线,
∴DF=BC,FE=AB,DE=AC;
∴DF+FE+DE=BC+AB+AC=(AB+BC+CA)=×18=9,
故选:B.
2.(4分)将点A(﹣2,3)平移到点B(1,﹣2)处,正确的移法是( )
A.向右平移3个单位长度,向上平移5个单位长度
B.向左平移3个单位长度,向下平移5个单位长度
C.向右平移3个单位长度,向下平移5个单位长度
D.向左平移3个单位长度,向上平移5个单位长度
【解答】解:点A(﹣2,3)平移到点B(1,﹣2)处,
∵﹣2+3=1,
3﹣5=﹣2,
∴平移方法为向右平移3个单位长度,向下平移5个单位长度.
故选:C.
3.(4分)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )
A. B. C.12 D.24
【解答】解:如图,设对角线相交于点O,
∵AC=8,DB=6,
∴AO=AC=×8=4,
BO=BD=×6=3,
由勾股定理的,AB===5,
∵DH⊥AB,
∴S菱形ABCD=AB•DH=AC•BD,
即5DH=×8×6,
解得DH=.
故选:A.
4.(4分)在图中,不能表示y是x的函数的是( )
A. B.
C. D.
【解答】解:A、对于每一个x的值,都有唯一一个y值与其对应,y是x的函数,故本选项错误;
B、对于每一个x的值,都有唯一一个y值与其对应,y是x的函数,故本选项错误;
C、对于每一个x的值,都有唯一一个y值与其对应,y是x的函数,故本选项错误;
D、对于每一个x的值,不都是有唯一一个y值与其对应,有时有多个y值相对应,所以y不是x的函数,故本选项准确.
故选:D.
5.(4分)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B.2 C.3 D.+2
【解答】解:∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=1,
又∵直角△BDE中,∠B=30°,
∴BD=2DE=2,
∴BC=CD+BD=1+2=3.
故选:C.
6.(4分)若实数a、b满足ab<0,则一次函数y=ax+b的图象可能是( )
A. B.
C. D.
【解答】解:因为ab<0,得到a<0,b>0或b<0,a>0,
当a<0,b>0,图象经过一、二、四象限;
当b<0,a>0,图象经过一、三、四象限,
故选:B.
7.(4分)大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90~110这一组的频率是( )
A.0.1 B.0.2 C.0.3 D.0.7
【解答】解:跳绳次数在90~110之间的数据有91,93,100,102四个,故频率为=0.2.
故选:B.
8.(4分)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A.12 B.24 C.12 D.16
【解答】解:在矩形ABCD中,
∵AD∥BC,
∴∠B′EF=∠EFB=60°,
由折叠的性质得∠A=∠A′=90°,A′E=AE=2,AB=A′B′,∠A′EF=∠AEF=180°﹣60°=120°,
∴∠A′EB′=∠A′EF﹣∠B′EF=120°﹣60°=60°.
在Rt△A′EB′中,
∵∠A′B′E=90°﹣60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2,即AB=2,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=AB•AD=2×8=16.
故选:D.
二、填空题(共8小题,每小题4分,满分32分)
9.(4分)圆周长公式C=2πR中,变量是 C和R .
【解答】解:∵在圆的周长公式C=2πR中,C与R是改变的,是变量;
∴变量是C,R,
故答案为C,R.
10.(4分)如图,在Rt△ABC中,∠ACB=90°,CD垂直于AB,垂足为点D,BC=AB,则∠DCB= 30° .
【解答】解:∵在Rt△ABC中,∠ACB=90°,BC=AB,
∴∠A=30°,
∴∠B=60°,
∵CD垂直于AB,垂足为点D,
∴∠CDB=90°,
∴∠DCB=30°,
故答案为:30°
11.(4分)一个多边形的内角和等于1080°,它是 八 边形.
【解答】解:设所求正n边形边数为n,
则1080°=(n﹣2)•180°,解得n=8.
故答案为:八.
12.(4分)如图,∠B=∠ACD=90°,BC=3,AB=4,CD=12,则AD= 13 .
【解答】解:在Rt△ABC中,∠ABC=90°,AB=4,BC=3,由勾股定理得:AC==5,
在Rt△ACD中,∠ACD=90°,AC=5,CD=12,由勾股定理得:AD==13,
故答案为:13.
13.(4分)在平面直角坐标系中,已知点P在第二象限,距离x轴3个单位长度,距离y轴2个单位长度,则点P的坐标为 (﹣2,3) .
【解答】解:∵点P在第二象限,距离x轴3个单位长度,距离y轴2个单位长度,
∴点P的横坐标为﹣2,纵坐标为3,
∴点P的坐标为(﹣2,3).
故答案为:(﹣2,3).
14.(4分)下列函数中:①y=﹣x;②y=;③y=﹣x2;④y=﹣x+3;⑤2x﹣3y=1.其中y是x的一次函数的是 ①④⑤ (填所有正确答案的序号).
【解答】解:①y=﹣x是正比例函数也是一次函数,故①正确;②y=是反比例函数,故②错误;③y=﹣x2是二次函数,故③错误;④y=﹣x+3是一次函数,故④正确;⑤2x﹣3y=1可变形为y=x﹣,是一次函数.
故答案为:①④⑤.
15.(4分)如图,在平行四边形ABCD中,BE平分∠ABC,交AD于点E,AB=3cm,ED=cm,则平行四边形ABCD的周长是 15cm .
【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD=3cm,AD=BC,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE=3cm,
∴AD=AE+DE=3+=4.5cm,
∴AD=BC=4.5cm,
∴平行四边形的周长是2(AB+BC)=2(3+4.5)=15(cm);
故答案为:15cm.
16.(4分)弹簧挂上物体后会伸长,测得﹣弹簧的长度y(cm)与所挂重物的质量x(㎏)有下面的关系:那么弹簧总长y(cm)与所挂重物x(㎏)之间的函数关系式为 y=0.5x+12 .
【解答】解:由表可知:常量为0.5;
所以,弹簧总长y(cm)与所挂重物x(㎏)之间的函数关系式为y=0.5x+12.
三、解答题(共7小题,满分56分)
17.(7分)如图,平行四边形ABCD的对角线AC=6cm,将平行四边形ABCD绕其对称中心旋转180°,求C点所转过的路径长.
【解答】解:C点所转的路径如图所示,
l===3πcm,
∴求C点所转过的路径长为3πcm.
18.(7分)如图,将△ABC先向上平移4个单位,再向左平移5个单位,它的像是△A′B′C′,写出△A′B′C′的顶点坐标,并作出该图形.
【解答】解:如图,A′(﹣2,3),B′(﹣4,2),C′(﹣2,0),△A′B′C′为所作.
19.(8分)如图,△ABC中,∠ACB=90°,D、E分别是BC、BA的中点,连接DE,F在DE延长线上,且AF=AE.
(1)求证:四边形ACEF是平行四边形;
(2)若四边形ACEF是菱形,求∠B的度数.
【解答】(1)证明:∵∠ACB=90°,E是BA的中点,
∴CE=AE=BE,
∵AF=AE,
∴AF=CE,
在△BEC中,∵BE=CE且D是BC的中点,
∴ED是等腰△BEC底边上的中线,
∴ED也是等腰△BEC的顶角平分线,
∴∠1=∠2,
∵AF=AE,
∴∠F=∠3,
∵∠1=∠3,
∴∠2=∠F,
∴CE∥AF,
又∵CE=AF,
∴四边形ACEF是平行四边形;
(2)解:∵四边形ACEF是菱形,
∴AC=CE,
由(1)知,AE=CE,
∴AC=CE=AE,
∴△AEC是等边三角形,
∴∠CAE=60°,
在Rt△ABC中,∠B=90°﹣∠CAE=90°﹣60°=30°.
20.(8分)在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间.
【解答】解:(1)由于蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.
故设y与x之间的函数关系式为y=kx+b(k≠0).
由图示知,该函数图象经过点(0,24),(2,12),则
,
解得.
故函数表达式是y=﹣6x+24.
(2)当y=0时,
﹣6x+24=0
解得x=4,
即蜡烛从点燃到燃尽所用的时间是4小时.
21.(8分)如图,某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,且距A点18海里,航行半小时后到达B点,此时测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.
(1)问B点是否在暗礁区域外?
(2)若继续向正东航行,有无触礁危险?请说明理由.
【解答】解:(1)作CD⊥AB于D点,设BC为x,
在Rt△BCD中,∠CBD=60°,
∴BD=x,CD=x,
在Rt△ACD中,∠CAD=30°,
tan∠CAD==,
∴=,
∴x=18,
∴B点不在暗礁区域内;
(2)∵CD=x=9,
∵9<16,
∴若继续向东航行船有触礁的危险.
22.(8分)2011年我市体卫站对某校九年级学生体育测试情况进行调研,从该校360名九年级学生中抽取了部分学生的成绩(成绩分为A、B、C三个层次)进行分析,绘制了频数分布表与频数分布直方图(如图),请根据图表信息解答下列问题:
分组 | 频数 | 频率 |
C | 10 | 0.10 |
B |
| 0.50 |
A | 40 |
|
合计 |
| 1.00 |
(1)补全频数分布表与频数分布直方图;
(2)如果成绩为A等级的同学属于优秀,请你估计该校九年级约有多少人达到优秀水平?
【解答】解:(1)如图
分组 | 频数 | 频率 |
C | 10 | 0.10 |
B | 50 | 0.50 |
A | 40 | 0.40 |
合计 | 100 | 1.00 |
(2)A等级的同学人数为40人,频率为0.40,
∴估计该校九年级约有 0.4×360=144人达到优秀水平.
23.(10分)在开展“美丽广西,清洁乡村”的活动中某乡镇计划购买A、B两种树苗共100棵,已知A种树苗每棵30元,B种树苗每棵90元.
(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,请你写出y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)如果购买A、B两种树苗的总费用不超过7560元,且B种树苗的棵数不少于A种树苗棵数的3倍,那么有哪几种购买树苗的方案?
(3)从节约开支的角度考虑,你认为采用哪种方案更合算?
【解答】解:(1)设购买A种树苗x棵,购买A、B两种树苗的总费用为y元,
y=30x+90(100﹣x)=9000﹣60x;
(2)设购买A种树苗x棵,则B种树苗(100﹣x)棵,根据题意得:
,
解得:24≤x≤25,
因为x是正整数,
所以x只能取25,24.
有两种购买树苗的方案:
方案一:购买A种树苗25棵时,B种树苗75棵;
方案二:购买A种树苗24棵时,B种树苗76棵;
(3)∵y=9000﹣60x,﹣60<0,
∴y随x的增大而减小,
又x=25或24,
∴采用购买A种树苗25棵,B种树苗75棵时更合算.
湘教版 八年级数学下学期期末模拟卷8(含解析): 这是一份湘教版 八年级数学下学期期末模拟卷8(含解析),共19页。
湘教版 八年级数学下学期期末模拟卷7(含解析): 这是一份湘教版 八年级数学下学期期末模拟卷7(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
湘教版 八年级数学下学期期末模拟卷6(含解析): 这是一份湘教版 八年级数学下学期期末模拟卷6(含解析),共15页。试卷主要包含了单项选择题,填空题,解答题等内容,欢迎下载使用。












