人教版七年级上册第四章 几何图形初步综合与测试教学设计

这是一份人教版七年级上册第四章 几何图形初步综合与测试教学设计，共6页。

1. 基本概念
（1）平面图形和立体图形
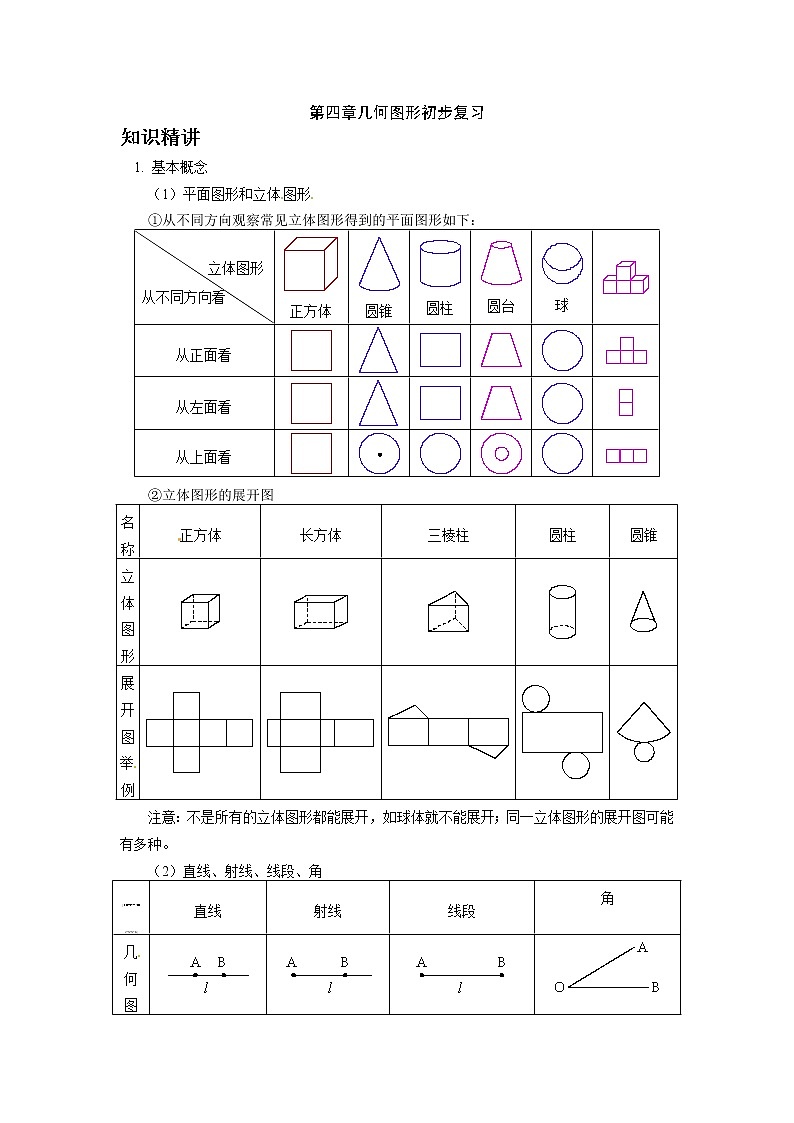
①从不同方向观察常见立体图形得到的平面图形如下：
②立体图形的展开图
注意：不是所有的立体图形都能展开，如球体就不能展开；同一立体图形的展开图可能有多种。
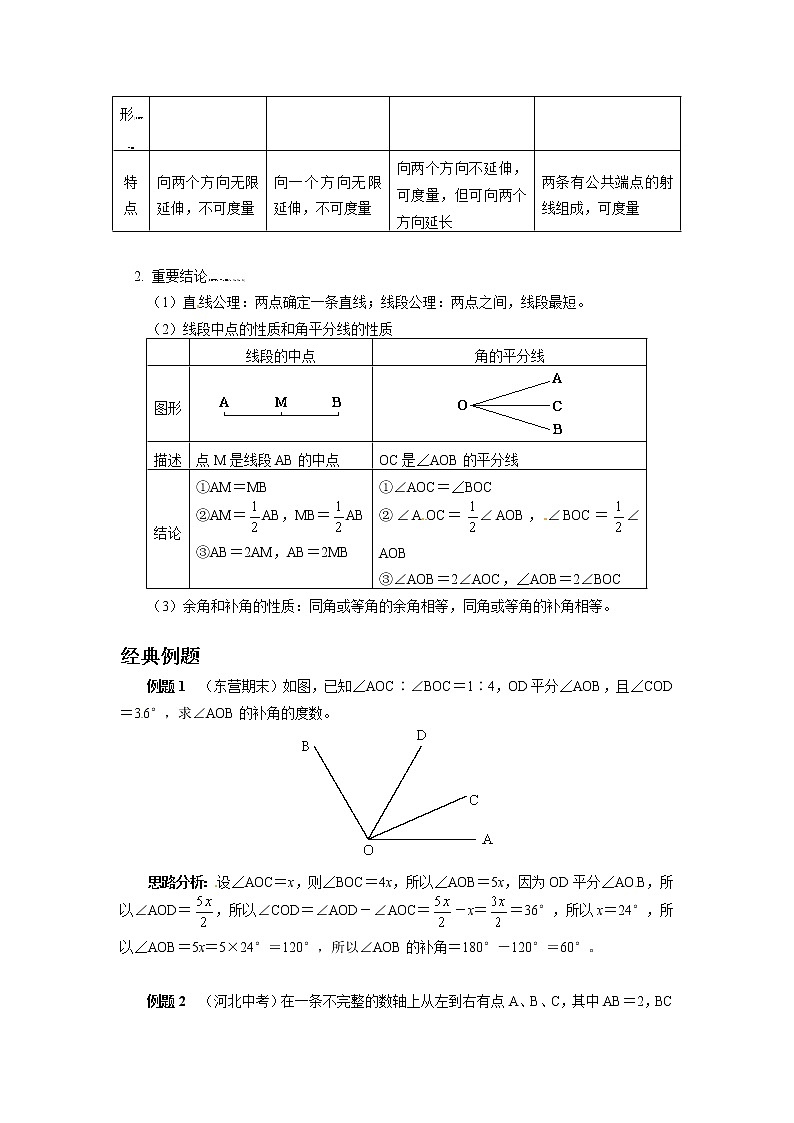
（2）直线、射线、线段、角
2. 重要结论[来源:学。科。网Z。X。X。K]
（1）直线公理：两点确定一条直线；线段公理：两点之间，线段最短。
（2）线段中点的性质和角平分线的性质
（3）余角和补角的性质：同角或等角的余角相等，同角或等角的补角相等。
经典例题
例题1 （东营期末）如图，已知∠AOC∶∠BOC＝1∶4，OD平分∠AOB，且∠COD＝36°，求∠AOB的补角的度数。
思路分析：设∠AOC＝x，则∠BOC＝4x，所以∠AOB＝5x，因为OD平分∠AOB，所以∠AOD＝，所以∠COD＝∠AOD－∠AOC＝－x＝＝36°，所以x＝24°，所以∠AOB＝5x＝5×24°＝120°，所以∠AOB的补角＝180°－120°＝60°。
例题2 （河北中考）在一条不完整的数轴上从左到右有点A、B、C，其中AB＝2，BC＝1，如图所示，设点A、B、C所对应的数的和是p。
（1）若以B为原点，写出点A、C所对应的数，并计算p的值；若以C为原点，p又是多少？
（2）若原点O在图中数轴上点C的右边，且CO＝28，求p。
思路分析：（1）若以B为原点，则A对应－2，C对应1，B对应0，所以p＝（－2）＋0＋1＝－1；若以C为原点，则A对应－3，B对应－1，C对应0，所以p＝（－3）＋（－1）＋0＝－4。
（2）根据题意A对应－31，B对应－29，C对应－28，所以p＝（－31）＋（－29）＋（－28）＝－88。
例题3 （宁城期末）如图所示，将平面图形折成一个正方体，得到的是如下四个图形中的（ ）
思路分析：“”与“”是在相对的两个面上，故选项B与D错误；由“”和“”的位置关系知选项A错误，故只有选项C正确。本题易出错的原因是没有弄清展开图折叠后的相对面及相邻面的图形位置。
答案：C
技巧点拨
利用方程思想求线段的长度或角的度数
在求线段的长度和角的度数问题时，通常把线段的长度或角的度数设为未知数，并根据所求的线段或角与其他线段或角之间的关系列方程求解。用方程来解几何问题能清楚简洁地表示出几何图形中的数量关系，是解决几何计算题的一种重要方法。
例：如下图，线段AB上有两点M、N，AM∶MB＝5∶11，点N是线段AB的中点，MN＝1.5，求AB的长度。
解析：设AM＝5x，则MB＝11x，AB＝16x，因为N是AB的中点，所以MN＝AN－AM＝AB－AM＝8x－5x＝3x，即3x＝1.5，所以x＝0.5，所以AB＝16x＝16×0.5＝8。
同步测试
（答题时间：20分钟）
1. 从左面看图中四个几何体，得到的图形是四边形的几何体共有（ ）
A. 1个B. 2个C. 3个D. 4个
*2. 如图所示，用量角器量几个角的度数，下列结论中正确的是（ ）
A. ∠BOC＝60°B. ∠COA是∠EOD的余角
C. ∠AOC＝∠BODD. ∠AOD与∠COE互补
**3. 下面等式成立的是（ ）
A. 83.5°＝83°50′B. 37°12′36″＝37.48°C. 24°24′24″＝24.44°D. 41.25°＝41°15′
4. 根据下面展开图，填写多面体的名称：
（1）__________，（2）__________，（3）__________。
*5. 如图所示，已知∠AOB∶∠BOC∶∠COD＝3∶2∶4，∠AOD＝108°，求∠AOB、∠BOC、∠COD的度数。
*6. 如图是一个正方体的平面展开图，标注了A字母的是正方体的正面，如果正方体的左面与右面标注的式子相等。
（1）求x的值。
（2）求正方体的上面和底面的数字和。
**7. 如图所示，已知线段AB＝80cm，M为AB的中点，P在MB上，N为PB的中点，且NB＝14cm，求PA的长。
参考答案
1. B 解析：从左面看，圆柱是四边形，圆锥是三角形，球是圆形，正方体是四边形，共2个，故选B。
*2. D 解析：A错误，∠BOC＝120°；B错误，∠COA＝60°，∠EOD＝60°，它们相等，不是互余关系；C错误，∠AOC＝60°，∠BOD＝30°，它们不相等；D正确，∠AOD＝150°，∠COE＝30°，它们互补，故选D。
**3. D 解析：A错误，83.5°＝83°30′；B错误，因为12′36″＝（）°＝0.21°，所以37°12′36″＝37.21°；C错误，24°24′24″≈24.41°，D正确，41.25°＝41°15′。
4.（1）长方体（2）三棱柱（3）三棱锥
*5. 解析：设∠AOB＝3x，则∠BOC＝2x，∠COD＝4x，则3x＋2x＋4x＋108°＝360°，解得x＝28°，所以3x＝84°，2x＝56°，4x＝112°即∠AOB＝84°，∠BOC＝56°，∠COD＝112°。
*6. 解析：正方体的表面展开图，相对的面之间一定相隔一个正方形，“A”与“－2”是相对面，“3”与“1”是相对面，“x”与“3x－2”是相对面。（1）因为正方体的左面与右面标注的式子相等，所以x＝3x－2，解得x＝1；（2）因为标注了A字母的是正方体的正面，所以上面和底面上的两个数字3和1，所以3＋1＝4。
**7. 解析：解法一：因为N是PB的中点，所以PB＝2NB，而NB＝14cm，所以PB＝2×14＝28cm，又因为M是AB的中点，所以AM＝MB＝AB，所以AM＝MB＝40cm，又因为MP＝MB－PB＝40－28＝12（cm），所以AP＝AM＋MP＝40＋12＝52（cm）。解法二：因为N是PB的中点，所以PB＝2NB，所以PB＝2×14＝28（cm），又因为AP＝AB－PB，AB＝80cm，所以AP＝80－28＝52（cm）。 立体图形
从不同方向看
正方体
圆锥
圆柱
圆台
球
从正面看
从左面看
从上面看
名称
正方体
长方体
三棱柱
圆柱
圆锥
立体图形
展开图
举例
[来源:学*科*网Z*X*X*K]
直线
射线
线段
角
几何图形[来源:学.科.网]
特点
向两个方向无限延伸，不可度量
向一个方向无限延伸，不可度量
向两个方向不延伸，可度量，但可向两个方向延长
两条有公共端点的射线组成，可度量
线段的中点
角的平分线
图形
描述
点M是线段AB的中点
OC是∠AOB的平分线
结论
①AM＝MB
②AM＝AB，MB＝AB
③AB＝2AM，AB＝2MB
①∠AOC＝∠BOC
②∠AOC＝∠AOB，∠BOC＝∠AOB
③∠AOB＝2∠AOC，∠AOB＝2∠BOC