





还剩37页未读,
继续阅读
2021-2022学年人教版数学中考专题复习之勾股定理课件PPT
展开
这是一份2021-2022学年人教版数学中考专题复习之勾股定理课件PPT,共45页。PPT课件主要包含了平方和,a2+b2c2等内容,欢迎下载使用。
考点一 直角三角形的性质【主干必备】1.直角三角形的两锐角_________. 2.直角三角形斜边上的中线等于斜边的_________.
3.直角三角形中,如果有一个角等于30°,那么30°角所对的直角边等于斜边的一半.
【微点警示】 1.前两个性质所有直角三角形都具有.2.性质3只适用于含30°角的直角三角形.
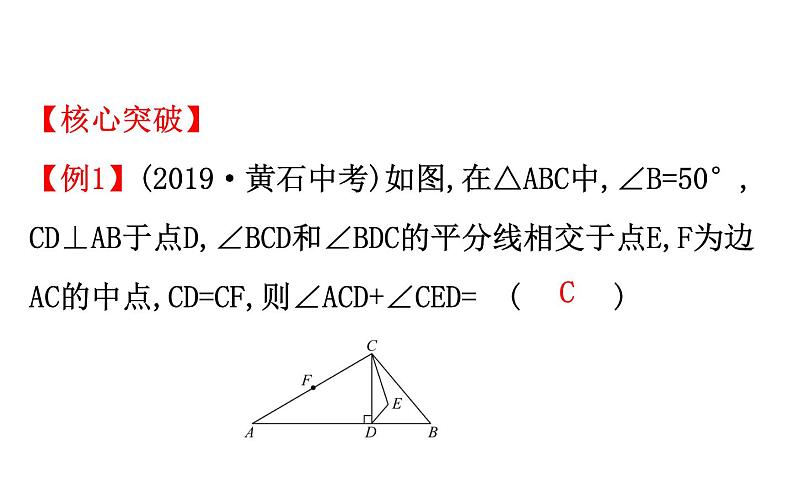
【核心突破】 【例1】(2019·黄石中考)如图,在△ABC中,∠B=50°,CD⊥AB于点D,∠BCD和∠BDC的平分线相交于点E,F为边AC的中点,CD=CF,则∠ACD+∠CED=( )
A.125°B.145°C.175°D.190°
【明·技法】直角三角形的性质 直角三角形除勾股定理外,还具有如下性质:(1)直角三角形两锐角互余.(2)直角三角形斜边的中线等于斜边的一半.
(3)直角三角形中30°的角所对的直角边等于斜边的一半.(4)如果直角三角形的一条直角边等于斜边的一半,那么这条直角边所对的锐角是30°.
(5)直角三角形的两直角边的乘积等于斜边与斜边上高的乘积.(6)直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.
【题组过关】1.已知在直角三角形ABC中,有一个锐角等于50°,则另一个锐角的度数是( ) A.30°B.40°C.45°D.50°
2.如图,在△ABC中,AB=AC,∠B=30°,AD⊥AB,交BC于点D,AD=4,则BC的长为( )A.8B.4C.12D.6
3.(2019·普陀区期末)如图,在△ABC中,AD⊥BC,垂足为点D,CE是边AB上的中线,如果CD=BE,∠B=40°,那么∠BCE=_______度.
4.(2019·苏州期末)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠ACB交AB于点E,EF⊥AB交CB于点F.
(1)求证:CD∥EF.(2)若∠A=70°,求∠FEC的度数.
【解析】(1)∵CD⊥AB,EF⊥AB,∴CD∥EF.(2)∵CD⊥AB,∠A=70°,∴∠ACD=90°-70°=20°,∵∠ACB=90°,CE平分∠ACB,∴∠ACE=45°,∴∠DCE=45°-20°=25°,∵CD∥EF,∴∠FEC=∠DCE=25°.
考点二 勾股定理 【主干必备】勾股定理:直角三角形两直角边的___________等于斜边的平方.
【微点警示】 勾股定理使用的前提是必须在直角三角形中.
【核心突破】 【例2】(2019·黔东南、黔西南、黔南中考)如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为______.
【例3】(原型题)(2018·东营中考)如图所示,圆柱的高AB=3,底面直径BC=3,现有一只蚂蚁想从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
【变形题1】如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径最短,则AC的长为______.
【变形题2】如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为_______cm(杯壁厚度不计).
【明·技法】利用勾股定理可以解决以下问题(1)已知直角三角形的两条边长求第三边长.(2)已知直角三角形的一边长,求另两条边之间的关系.(3)用于证明线段平方关系.
(4)解决最短距离问题.(5)解决与折叠有关的问题.
【题组过关】1.(2019·深圳龙华区期末)在Rt△ABC中,∠C=90°,AC=9,BC=12,则AB边上的高是( )
2.如图所示是一个三级台阶,它的每一级的长、宽、高分别等于55 cm,10 cm,6 cm,A和B是这两个台阶的两个相对的端点,则一只蚂蚁从点A出发经过台阶爬到点B的最短路线长为_______cm.
3.(2019·朔州期末)限速安全驾,文明靠大家,根据道路管理条例规定,在某段笔直的公路L上行驶的车辆,限速60千米/时.一观测点M到公路L的距离MN为30米,现测得一辆汽车从A点到B点所用时间为5秒,已知观测点M到A,B两点的距离分别为50米、34米,通过计算判断此车是否超速.
【解析】∵在Rt△AMN中,AM=50,MN=30,∴AN= =40(米),∵在Rt△MNB中,BM=34,MN=30,∴BN= =16(米),∴AB=AN+NB=40+16=56(米),
∴汽车从A到B的平均速度为56÷5=11.2(米/秒),∵11.2米/秒=40.32千米/时<60千米/时,∴此车没有超速.
考点三 勾股定理的逆定理 【主干必备】勾股定理的逆定理:如果三角形的三边长a,b,c满足____________,那么这个三角形是直角三角形.
【微点警示】 1.勾股定理的逆定理是从边的角度判定直角三角形.2.从角的角度:有一个直角的三角形是直角三角形或两锐角互余的三角形是直角三角形.
【核心突破】 【例4】(2019·滨州中考)满足下列条件时,△ABC不是直角三角形的为( )A.AB= BC=4,AC=5B.AB∶BC∶AC=3∶4∶5
C.∠A∶∠B∶∠C=3∶4∶5D.|cs A- |+ =0
【明·技法】运用勾股定理的逆定理的三个步骤1.确定最长边.2.计算最长边的平方以及其他两边的平方和.3.判断最长边的平方是否与其他两边的平方和相等,若相等,则此三角形为直角三角形,否则不是直角三角形.
【题组过关】1.(2019·三明质检)下列各组数中是勾股数的是 ( ) A.4,5,6B.0.3,0.4,0.5C.1,2,3D.5,12,13
2.下列各组数中,能构成直角三角形的是( )A.4,5,6B.1,1, C.6,8,11D.5,12,23
3.(2019·温州苍南县期中)如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD=_______度.
4.(2019·兰州期末)如图,在四边形ACBD中,∠C=90°,AC=3,BC=4,AD=12,BD=13.连接AB,求证:AD⊥AB.
5.(2019·镇江期中)已知:如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为点D,交AB于点E,且BE2-EA2=AC2.
(1)求证:∠A=90°.(2)若AB=8,BC=10,求AE的长.
【解析】(1)连接CE,如图,∵点D是BC的中点,DE⊥BC,∴CE=BE,∵BE2-EA2=AC2,∴CE2-EA2=AC2,∴EA2+AC2=CE2,∴△ACE是直角三角形,且∠A=90°.
考点一 直角三角形的性质【主干必备】1.直角三角形的两锐角_________. 2.直角三角形斜边上的中线等于斜边的_________.
3.直角三角形中,如果有一个角等于30°,那么30°角所对的直角边等于斜边的一半.
【微点警示】 1.前两个性质所有直角三角形都具有.2.性质3只适用于含30°角的直角三角形.
【核心突破】 【例1】(2019·黄石中考)如图,在△ABC中,∠B=50°,CD⊥AB于点D,∠BCD和∠BDC的平分线相交于点E,F为边AC的中点,CD=CF,则∠ACD+∠CED=( )
A.125°B.145°C.175°D.190°
【明·技法】直角三角形的性质 直角三角形除勾股定理外,还具有如下性质:(1)直角三角形两锐角互余.(2)直角三角形斜边的中线等于斜边的一半.
(3)直角三角形中30°的角所对的直角边等于斜边的一半.(4)如果直角三角形的一条直角边等于斜边的一半,那么这条直角边所对的锐角是30°.
(5)直角三角形的两直角边的乘积等于斜边与斜边上高的乘积.(6)直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.
【题组过关】1.已知在直角三角形ABC中,有一个锐角等于50°,则另一个锐角的度数是( ) A.30°B.40°C.45°D.50°
2.如图,在△ABC中,AB=AC,∠B=30°,AD⊥AB,交BC于点D,AD=4,则BC的长为( )A.8B.4C.12D.6
3.(2019·普陀区期末)如图,在△ABC中,AD⊥BC,垂足为点D,CE是边AB上的中线,如果CD=BE,∠B=40°,那么∠BCE=_______度.
4.(2019·苏州期末)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠ACB交AB于点E,EF⊥AB交CB于点F.
(1)求证:CD∥EF.(2)若∠A=70°,求∠FEC的度数.
【解析】(1)∵CD⊥AB,EF⊥AB,∴CD∥EF.(2)∵CD⊥AB,∠A=70°,∴∠ACD=90°-70°=20°,∵∠ACB=90°,CE平分∠ACB,∴∠ACE=45°,∴∠DCE=45°-20°=25°,∵CD∥EF,∴∠FEC=∠DCE=25°.
考点二 勾股定理 【主干必备】勾股定理:直角三角形两直角边的___________等于斜边的平方.
【微点警示】 勾股定理使用的前提是必须在直角三角形中.
【核心突破】 【例2】(2019·黔东南、黔西南、黔南中考)如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为______.
【例3】(原型题)(2018·东营中考)如图所示,圆柱的高AB=3,底面直径BC=3,现有一只蚂蚁想从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
【变形题1】如图,一只蚂蚁沿着棱长为2的正方体表面从点A出发,经过3个面爬到点B,如果它运动的路径最短,则AC的长为______.
【变形题2】如图,圆柱形玻璃杯高为14 cm,底面周长为32 cm,在杯内壁离杯底5 cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3 cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为_______cm(杯壁厚度不计).
【明·技法】利用勾股定理可以解决以下问题(1)已知直角三角形的两条边长求第三边长.(2)已知直角三角形的一边长,求另两条边之间的关系.(3)用于证明线段平方关系.
(4)解决最短距离问题.(5)解决与折叠有关的问题.
【题组过关】1.(2019·深圳龙华区期末)在Rt△ABC中,∠C=90°,AC=9,BC=12,则AB边上的高是( )
2.如图所示是一个三级台阶,它的每一级的长、宽、高分别等于55 cm,10 cm,6 cm,A和B是这两个台阶的两个相对的端点,则一只蚂蚁从点A出发经过台阶爬到点B的最短路线长为_______cm.
3.(2019·朔州期末)限速安全驾,文明靠大家,根据道路管理条例规定,在某段笔直的公路L上行驶的车辆,限速60千米/时.一观测点M到公路L的距离MN为30米,现测得一辆汽车从A点到B点所用时间为5秒,已知观测点M到A,B两点的距离分别为50米、34米,通过计算判断此车是否超速.
【解析】∵在Rt△AMN中,AM=50,MN=30,∴AN= =40(米),∵在Rt△MNB中,BM=34,MN=30,∴BN= =16(米),∴AB=AN+NB=40+16=56(米),
∴汽车从A到B的平均速度为56÷5=11.2(米/秒),∵11.2米/秒=40.32千米/时<60千米/时,∴此车没有超速.
考点三 勾股定理的逆定理 【主干必备】勾股定理的逆定理:如果三角形的三边长a,b,c满足____________,那么这个三角形是直角三角形.
【微点警示】 1.勾股定理的逆定理是从边的角度判定直角三角形.2.从角的角度:有一个直角的三角形是直角三角形或两锐角互余的三角形是直角三角形.
【核心突破】 【例4】(2019·滨州中考)满足下列条件时,△ABC不是直角三角形的为( )A.AB= BC=4,AC=5B.AB∶BC∶AC=3∶4∶5
C.∠A∶∠B∶∠C=3∶4∶5D.|cs A- |+ =0
【明·技法】运用勾股定理的逆定理的三个步骤1.确定最长边.2.计算最长边的平方以及其他两边的平方和.3.判断最长边的平方是否与其他两边的平方和相等,若相等,则此三角形为直角三角形,否则不是直角三角形.
【题组过关】1.(2019·三明质检)下列各组数中是勾股数的是 ( ) A.4,5,6B.0.3,0.4,0.5C.1,2,3D.5,12,13
2.下列各组数中,能构成直角三角形的是( )A.4,5,6B.1,1, C.6,8,11D.5,12,23
3.(2019·温州苍南县期中)如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.则∠ACD=_______度.
4.(2019·兰州期末)如图,在四边形ACBD中,∠C=90°,AC=3,BC=4,AD=12,BD=13.连接AB,求证:AD⊥AB.
5.(2019·镇江期中)已知:如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为点D,交AB于点E,且BE2-EA2=AC2.
(1)求证:∠A=90°.(2)若AB=8,BC=10,求AE的长.
【解析】(1)连接CE,如图,∵点D是BC的中点,DE⊥BC,∴CE=BE,∵BE2-EA2=AC2,∴CE2-EA2=AC2,∴EA2+AC2=CE2,∴△ACE是直角三角形,且∠A=90°.












