人教版八年级上册11.1.1 三角形的边学案设计

这是一份人教版八年级上册11.1.1 三角形的边学案设计，共4页。学案主要包含了三角形及其相关概念，三角形的分类，探究三角形的三边关系，自主训练，巩固提高，课堂小结，反思质疑，课堂检测，课后作业，分层巩固等内容，欢迎下载使用。
班级 姓名 学号
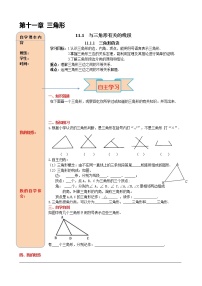
学习目标:
1.理解三角形的定义及相关概念.
2.能将三角形分别按角、边分类.
3.知道并能证明三角形的三边关系，会判断三条线段能否组成三角形.
4.经历定义的探索和三角形的分类以及三边关系的推导过程。在学习的过程中，学会独立思考、与人交流共享，并与同伴得到共同提高.
教学重点、难点：
重点：三角形的有关概念，能用符号语言表示三角形，三角形的三边关系．
难点：三边关系的推导及应用．
教学过程：
一、三角形及其相关概念
1.在原有基础上理解三角形的定义；
设问： (1)判断：以下图形是三角形吗？
⑶什么样的图形叫做三角形？
（设计意图：通过播放生活中的图片，从图形中抽象出三角形，通过观察几何图形体验三角形的特征，从而尝试得出三角形的定义）
定义：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2.结合图形认识三角形的基本要素及表示方法.（边、顶点、内角，对边、对角，表示法.）
（设计意图：让学生通过图形观察三角形的组成，自主得出三角形的相关概念。）
A
D
C
B
E
3.练习：
（1）图中有几个三角形？用符号表示这些三角形.
(2)以AB为边的三角形有哪些？
(3)以E为顶点的三角形有哪些？
(4)说出其中ΔBCD的三个角.
二、三角形的分类
设问：同学们已经知道哪些形状的三角形？
根据定义的不同角度，如何将三角形进行分类？说说你的分类标准和理由.
（先独立思考再在小组内交流，最后全班交流）
按角分类； ⑵按边分类.
锐角三角形 三边都不等的三角形
三角形 直角三角形 三角形 底边和腰不相等的等腰三角形
钝角三角形 等腰三角形
等边三角形
（设计意图：通过对已有知识的回忆和归纳，提示学生分类的数学思想，引导学生按不同标准对三角形进行分类）
三、探究三角形的三边关系
B
C
A
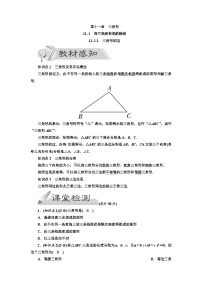
1. 议一议：如图三角形中，假设有一只小虫要从点B出发沿着三角形的边爬到点C，它有几条路线可以选择？各条路线的长一样吗？
问题：在一个三角形中，任意两边之和与第三边的长度有怎样的关系？为什么？以上不等式移项，可得到什么结论？
（设计意图：通过设置具体情境，激发学生解决实际问题的兴趣和）
三角形的三边关系：三角形两边的和大于第三边，三角形两边的差小于第三边
2.下列每组数分别是三根小木棒的长度，用它们能构成三角形吗？
⑴5cm,3cm,2cm； ⑵5cm,2cm,1cm； ⑶5cm,3cm,4cm.
追问：⑴你是怎样判断的？⑵你能总结出一条比较简便的判断方法吗？
结论：两条较短线段之和大于最长的线段时可构成三角形.
(设计意图：加深对三角形三边关系的理解，运用三边关系解决实际问题)
3.下列长度的三条线段能否构成三角形？
（1）3cm，4cm，8cm； （2）2a，3a，4a；
（3）0.3cm，0.2cm，0.4cm； （4）a：b：c=1:4:3
（设计意图：经历已知不同条件的线段长度，由特殊值推广到更一般的情形。）
四、自主训练，巩固提高
例 用一条长度为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边的2倍，那么各边长是多少？
(2)能围成有一边长为4cm的等腰三角形吗?为什么？
（设计意图：巩固三边关系的知识，运用三角形的三边关系解决实际应用）
五、课堂小结，反思质疑
1.什么样的图形叫三角形?
2.如何将三角形进行分类?
3.如何判断三条线段能否构成三角形？你是如何理解的?
4.你体会到哪些重要的数学思想方法?
六、课堂检测
达标检测：
【A组】（100分）
1．三角形的任意两边之和 第三边；任意两边之差 第三边．
2．现有两根木棒，它们的长度分别为20 cm和30 cm，若不改变木棒的长度，要钉成一个三角形木架，应在下列四根木棒中选取( )
A．10 cm的木棒 B．20 cm的木棒
C．50 cm的木棒 D．60 cm的木棒
3．用下列长度的三条线段能构成三角形的是（ ）
A．6cm、3cm、2cm B．5.5cm、2.4cm、3.1cm
C．2.5cm、3cm、2cm D．7cm、3cm、4cm
4．以长为3cm、5cm、7cm、10cm的四条线段中的三条为边能构成三角形的个数为（ ）
A．1 B．2 C．3 D．4
5．已知等腰三角形的两边长分别为3和6，则它的周长为( )
A．9 B．12 C．15 D．12或15
【B组】（20分）
等腰三角形的周长为20cm，腰长为xcm，则x在什么范围内？
七、课后作业，分层巩固
必做题：教科书P8/第1、2、6、7题.
选做题：1.教科书P29/第9题.
2.等腰三角形的周长为20cm，底边为xcm，则x在什么范围内？