初中数学人教版八年级上册第十一章 三角形11.3 多边形及其内角和11.3.2 多边形的内角和教学设计及反思
展开【课标内容】
1.获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验.
2.体会数学知识之间、数学与其他学科之间、数学与生活之间的联系,运用数学的思维方式进行思考,增强发现和提出问题的能力、分析和解决问题的能力.
3.了解数学的价值,提高学习数学的兴趣,增强学好数学的信心,养成良好的学习习惯,具有初步的创新意识和科学态度.
4.探索多边形的内角和定理.
【教材分析】
本节课是以三角形的内角和知识为基础,通过组织学生观察、类比、推理等数学活动,引导学生探索多边形的内角和与外角和的公式.通过多种转化方法的探究让学生深刻体验化归思想,以及分类、数形结合的思想,从特殊到一般的认识问题的方法,发展学生合情推理能力和语言表达能力.
【学情分析】
教材先是通过作对角线探求任意四边形内角和.这个环节,通过自主学习环节的铺垫及学生的现有知识,把未知的四边形内角和转化为已知的三角形内角和来求解,有效地突破本节课的难点.再作对角线探求五边形、六边形的内角和,找规律探求n边形的内角和公式.这里我增加了一个环节是通过从一个顶点出发作对角线,来达到分割为三角形的目的.从边上、五边形内、外的任意一点出发,与顶点连接,来分割三角形.这个环节我没有直接把方法教授给学生,而是让学生先在学案上自主探索,然后小组合作,探讨,交流,小组汇报展示探索方法.这么做,可以锻炼学生合作交流的能力,同时可以提高语言表达能力.
【教学目标】
1.使学生了解多边形的内角、外角等概念.
2.能通过不同方法探索多边形的内角和与外角和公式,并会应用它们进行有关计算.
【教学重点】
多边形的外角和定理及其应用
【教学难点】
多边形的外角和定理的推导
【教学方法】
五步教学法、引导探究法
【课前准备】
三角板、多媒体
【课时设置】
一课时
【教学过程】
一、预学自检 互助点拨
(阅读教材P21-23,完成以下问题)
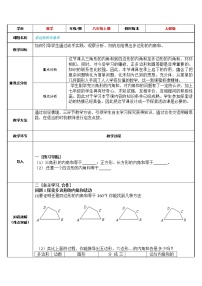
如图,从四边形的一个顶点出发可以引几条对角线?它们将四边形分成几个三角形? 那么四边形的内角和等于多少度?A
B
C
D第2题
A
B
C
D
A
B
C
D
可以引一条对角线;它将四边形分成两个三角形;因此,四边形的内角和=△ABD的内角和+△BDC的内角和=2×180°=360°.
类似地,你能知道五边形、六边形…… n边形的内角和是多少度吗?
你能得到多边形内角和公式吗?
设多边形的边数为n,则n边形的内角和等于_________
(2)除利用对角线把多边形分成几个三角形外,还有其他的分法吗?你会用新的分法得到n边形的内角和公式吗?
【设计意图】 从简单的四边形入手,让学生亲自操作寻求结论,易于引起学习兴趣,鼓励学生找到多种方法,让学生体会多种分割形式,有利于深入领会转化的本质——四边形转化为三角形,也让学生体验数学活动充满探索和解决问题方法的多样性.通过交流,让学生用自己的语言清楚地表达解决问题的过程,可以提高语言表达能力.
二、合作互学 探究新知
1. 已知:四边形ABCD的∠A+∠C=180°.求:∠B与∠D的关系.
2. 如图,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等于多少?
【设计意图】 让学生运用所学知识解决问题,提高解决问题的能力,鼓励学生畅所欲言总结对本节课的收获和体会,有利于培养归纳、总结的习惯和能力,让学生自主建构知识体系.
三、自我检测 成果展示
(一)判断题
1.当多边形边数增加时,它的内角和也随着增加.( )
2.当多边形边数增加时.它的外角和也随着增加.( )
3.从n边形一个顶点出发,可以引出(n一2)条对角线,得到(n一2)个三角形.( )
(二)填空题
1.一个多边形的每一个外角都等于30°,则这个多边形为________边形.
2.一个多边形的每个内角都等于135°,则这个多边形为 ________ 边形.
3.内角和等于外角和的多边形是 ________边形.
4.若多边形内角和等于外角和的3倍,则这个多边形是 ________边形.
5.五边形的对角线有 ________条,它们内角和为________.
6.多边形每个内角都相等,内角和为720°,则它的每一个外角为 ________.
(三)选择题
1.多边形的每个外角与它相邻内角的关系是( )
A.互为余角 B.互为邻补角
C.两个角相等 D.外角大于内角
2.一个多边形的内角和为720°,那么这个多边形的对角线条数为( )
A.6条 B.7条 C.8条 D.9条
3.随着多边形的边数n的增加,它的外角和( )
A.增加 B.减小 C.不变 D.不定
4.多边形的内角和为它的外角和的4倍,这个多边形是( )
A.八边形 B.九边形 C.十边形 D,十一边形
四、应用提升 挑战自我
1.一个多边形的内角和是它的外角和的4倍,求这个多边形的边数.
2.多边形的一个内角的外角与其余内角的和为600°,求这个多边形的边数.
(【设计意图】 充分利用多媒体资源帮助学生理解、消化、新的知识,能够灵活的运用这节课所学习的内容.)
五、经验总结 反思收获
本节课你学到了什么____________________________________
【设计意图】 师生共同回忆所学内容,共同小结,渐渐补充.充分利用学案资源帮助学生理解、消化、新的知识,能够灵活的运用这节课所学习的内容.教师引导学生总结今天学习的主要内容,在学习后进行适当总结有助于学生更加深刻理解内容.
【板书设计】
多边形
多边形内角和是360度
正多边形
【备课反思】
本节课从实际问题入手,在引课时出示了多幅日常生活用品和建筑的图片,加强了数学与实际生活的联系,让学生感到数学离自己很近,激发了学生的求知欲.创设了良好的教学氛围.其次注重让学生在学习活动中领悟数学思想方法.数学的思想方法比有限的数学知识更为重要.学生在探索多边形内角和的过程中先把五边形转化成三角形.进而求出内角和,这体现了由未知转化为已知的思想.特别是在课堂教学中适时的利用问题加以引导,使学生领会数学思想方法,真正理解和掌握数学的知识、技能,增强空间观念及数学思考能力培养,并获得数学活动经验.同时,恰当的使用课件扩大了课堂容量,使课堂教学的深度和广度都有所提高.课件的使用提高了课堂效率,为学生的探索讨论赢得了时间.同时也加大了练习量,有助于学生知识可巩固和提高.
整节课学生的情绪饱满,思维活跃,在教师适当的引导下,学生能够合作交流和自主探究,成功的利用四种方法探索出了多边形的内角和公式,较好的完成了本节课的教学目标.
初中人教版11.3.2 多边形的内角和教学设计及反思: 这是一份初中人教版11.3.2 多边形的内角和教学设计及反思,共6页。教案主要包含了教材分析,教学目标分析,教法和学法分析,教学过程分析,评价分析,设计说明等内容,欢迎下载使用。
人教版八年级上册11.3.2 多边形的内角和教学设计及反思: 这是一份人教版八年级上册11.3.2 多边形的内角和教学设计及反思,共3页。
初中数学人教版八年级上册13.1.1 轴对称教学设计及反思: 这是一份初中数学人教版八年级上册13.1.1 轴对称教学设计及反思,共8页。教案主要包含了课标内容,教材分析,学情分析,教学目标,教学重点,教学难点,教学方法,课前准备等内容,欢迎下载使用。