初中数学人教版八年级上册11.3.2 多边形的内角和教学设计及反思
展开11.3.2 多边形的内角和
教学目标
1.能通过不同的方法探索多边形的内角和与外角和公式.
2.能利用多边形的内角和与外角和公式进行有关计算.
预习反馈
阅读教材P21~23,完成预习内容.
问题1:你知道三角形的内角和是多少度吗?
解:三角形的内角和等于180°.
问题2:你知道任意一个四边形的内角和是多少度吗?
学生展示探究成果
方法1:分成2个三角形 180°×2=360°
方法2:分割成4个三角形 180°×4-360°=360°
方法3:分割成3个三角形 180°×3-180°=360°
【点拨】 从一个顶点出发和各顶点相连,把四边形的问题转化为三角形的问题.
问题3:你知道五边形的内角和是多少度吗?
问题4:你知道六边形、七边形的内角和分别是多少度吗?
知识探究:n边形的内角和等于(n-2)×180°.
问题5:n边形的每一个外角与它相邻的内角之和是多少度?
解:180°.
问题6:n边形的内角和与外角和加起来等于多少度?
解:180°n.
知识探究:多边形的外角和等于360°.
名校讲坛
例1 (教材P22例1变式)如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:如图,在四边形ABCD中,
∠A+∠C=180°.
∵∠A+∠B+∠C+∠D=(4-2)×180°=360°,
∴∠B+∠D=360°-(∠A+∠C)=360°-180°=180°.
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
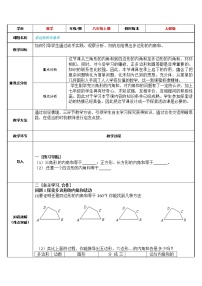
【跟踪训练1】 (《名校课堂》11.3.2习题)求如图所示的图形中x的值.
解:(1)根据图形可知:x=360-150-90-70=50.
(2)根据图形可知:x=180-[360-(90+73+82)]=65.
(3)根据图形可知:x+x+30+60+x+x-10=(5-2)×180.解得x=115.
例2 (教材P24练习T3)一个多边形的内角和与外角和相等,它是几边形?
解:因为多边形的外角和为360°,设它是n边形,
则(n-2)×180°=360°,解得n=4.
答:它是四边形.
【跟踪训练2】 (《名校课堂》11.3.2习题)一个多边形的各个内角都相等,其中一个外角等于与它相邻的内角的,求这个多边形的边数.
解:设这个多边形的一个内角为x,外角为x.
根据题意,得x+x=180°.
解得x=108°,x=72°.
360°÷72°=5.
答:这个多边形的边数为5.
巩固训练
1.八边形的内角和为(C)
A.180° B.360° C.1 080° D.1 440°
2.已知一个多边形的内角和是900°,则这个多边形是(C)
A.五边形 B.六边形 C.七边形 D.八边形
3.下列四个选项中,不是多边形内角和的是(C)
A.360° B.540° C.600° D.2 160°
4.已知一个正多边形的每个外角都等于60°,则这个多边形是(B)
A.正五边形 B.正六边形
C.正七边形 D.正八边形
5.已知一个多边形的内角和等于它的外角和,则这个多边形的边数是4.
6.一个多边形内角和的度数比外角和的度数的4倍多180°,求这个多边形的边数.
解:设这个多边形的边数为n,则(n-2)×180°-4×360°=180°,解得n=11.
∴这个多边形是十一边形.
7.如图所示,四边形ABCD中,∠A+∠B=222°,且∠ADC,∠DCB的平分线相交于点O,求∠COD的度数.
解:∵四边形的内角和为360°,∠A+∠B=222°,
∴∠ADC+∠BCD=138°.
∵OD平分∠ADC,OC平分∠BCD,
∴∠ODC+∠OCD=69°.
∴∠COD=111°.
8.如图所示,已知△ABC为直角三角形,∠B=90°.若沿图中虚线剪去∠B,则∠1+∠2的度数是多少?
解:∵∠B=90°,∴∠A+∠C=90°.
∴∠1+∠2+∠A+∠C=360°.
∴∠1+∠2=270°.
课堂小结
1.通过三角形向四边形、五边形…的转化,体会转化思想在几何中的运用,体会从特殊到一般的认识问题的方法.
2.能利用多边形的内角和与外角和公式进行有关计算.
初中人教版11.3.2 多边形的内角和教学设计及反思: 这是一份初中人教版11.3.2 多边形的内角和教学设计及反思,共6页。教案主要包含了教材分析,教学目标分析,教法和学法分析,教学过程分析,评价分析,设计说明等内容,欢迎下载使用。
人教版八年级上册11.3.2 多边形的内角和教学设计及反思: 这是一份人教版八年级上册11.3.2 多边形的内角和教学设计及反思,共3页。
初中数学人教版八年级上册第十一章 三角形11.3 多边形及其内角和11.3.1 多边形教案: 这是一份初中数学人教版八年级上册第十一章 三角形11.3 多边形及其内角和11.3.1 多边形教案,共3页。