初中数学人教版八年级上册11.3.2 多边形的内角和教案设计

这是一份初中数学人教版八年级上册11.3.2 多边形的内角和教案设计，共4页。

掌握多边形的内角和的计算方法，并能用内角和知识解决一些较简单的问题；
通过多边形内角和计算公式的推导，培养学生探索与归纳能力
多边形的内角和以及外角和
自主探究
探究点一：多边形的内角和
例1、一个多边形的内角和为1800°，截去一个角后，得到的多边形的内角和为( )
A．1620° B．1800°
C．1980° D．以上答案都有可能
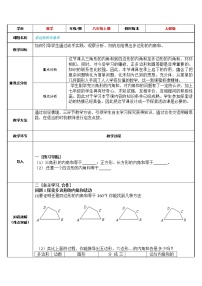
例2、如图，∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝( )
A．450° B．540°
C．630° D．720°
探究点二：多边形的外角和
例3、一个多边形的内角和与外角和的和为540°，则它是( )
A．五边形 B．四边形
C．三角形 D．不能确定
尝试应用
1.某学生在计算四个多边形的内角和时，得到下列四个答案，其中错误的是（ ）
A.180° B.540° C.1900° D.1080°
2.如果一个多边形的内角和是720°，那么这个多边形的对角线的条数是（ ）
Ａ.6 Ｂ.9 Ｃ.14 Ｄ.20
3.正多边形的一个外角的度数为36°，则这个正多边形的边数为( )
A.6 B.8 C.10 D.12
4.多边形的内角和不可能为( )
A.180° B.680° C.1080° D.1980°
5．一个多边形截去一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为（ ）
6．已知正n边形的一个内角为135°，则边数n的值是（ ）

7．若一个多边形的内角和小于其外角和，则这个多边形的边数是（ ）
8．正十二边形每个内角的度数为 _________ ．
9．如果一个正多边形的一个外角是60°，那么这个正多边形的边数是 _________ ．
10．若一个多边形内角和等于1260°，则该多边形边数是 _________ ．
11、一个多边形的内角和是外角和的2倍，则这个多边形的边数为 _________ ．
12.如果一个多边形的内角和等于它的外角和5倍，那么这个多边形是____边形。
13.若n边形的每个内角都是150°，则n=____。
14.一个多边形的每个外角都是36°，这个多边形是______边形。
15.如果一个多边形的每个内角都相等，且内角的度数是与它相邻的外角度数的2倍，那么这个边形的每个内角是_____度，其内角和等于______度。
16．一个多边形截去一个角（不过顶点）后，所形成的一个多边形的内角和是2520°，求原多边形的边数。

17．若一个多边形除了一个内角外，其余各内角之和为2570°，求这个内角的度数。
18．若多边形的所有内角与它的一个外角的和为600°，求边数和内角和．
19. 已知一个多边形，它的外角和等于内角和的四分之—，求这个多边形的边数.
课堂小结
通过今天的学习，你有什么收获？
课后作业
A．
5
B．
5或6
C．
5或7
D．
5或6或7

A．
6
B．
7
C．
8
D．
10

A．
3
B．
4
C．
5
D．
6