冀教版九年级上册第28章 圆28.3 圆心角和圆周角第3课时课时训练

这是一份冀教版九年级上册第28章 圆28.3 圆心角和圆周角第3课时课时训练，共7页。

知识点 1 同弧(或等弧)所对的圆周角相等
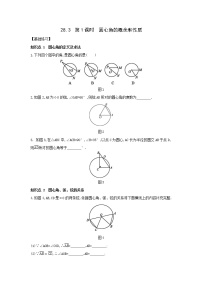
1.如图1,A,B,C,D是圆上的点,AB,CD交于点E,则图中与∠A相等的角是( )
A.∠B B.∠C C.∠DEB D.∠D

图1 图2
2.[教材练习第2题变式] 如图2,△ABC内接于☉O,∠ABC=71°,∠CAB=53°,点D在☉O上,则∠ADB的度数为( )
A.45° B.53° C.56° D.71°
3.如图3,在△ABC中,AB=AC,以AB为直径的☉O交BC于点D,延长CA交☉O于点E,连接ED,则△CDE是 三角形(填“等腰”或“等边”或“直角”).
图3
4.如图4,AB是☉O的直径,CD是☉O的弦,如果∠ACD=30°.
(1)求∠BAD的度数;
(2)若AD=3,求DB的长.
图4
知识点 2 圆内接四边形及其性质
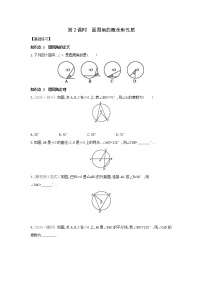
5.[2020·吉林] 如图5,四边形ABCD内接于☉O,若∠B=108°,则∠D的大小为( )
A.54° B.62° C.72° D.82°

图5 图6
6.如图6,四边形ABCD内接于☉O,点E在BC的延长线上.若∠BOD=120°,则∠DCE=
°.
7.[教材练习第1题变式] 如图7,四边形ABCD是☉O的内接四边形,BC是☉O的直径,∠ACB=20°,D为AC的中点,求∠DAC的度数.
图7
8.如图8,已知A,B,C,D是☉O上的四点,延长DC,AB相交于点E,BC=BE.
求证:△ADE是等腰三角形.
图8
【能力提升】
9.在圆内接四边形ABCD中,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )
A.60° B.80° C.100° D.120°
10.[2020·赤峰] 如图9,☉A经过平面直角坐标系的原点O,交x轴于点B(-4,0),交y轴于点C(0,3),点D为第二象限内圆上一点,则∠CDO的正弦值是( )
图9
A.35 B.-34 C.34 D.45
11.如图10,在世界杯足球比赛中,甲带球向对方球门PQ进攻,当他带球冲到点A时,同伴乙已经冲到点B.有两种射门方式:第一种是甲直接射门;第二种是甲将球传给乙,由乙射门.仅从射门角度考虑,应选择第 种射门方式.

图10 图11
12.如图11,四边形ABCD内接于☉O,且四边形OABC是平行四边形,则∠D= °.
13.如图12,四边形ABCD内接于☉O,点E在对角线AC上,且EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
图12
14.如图13,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是△ABC的外接圆的直径,∠EAC=120°,BC=6cm,求AD的长.
图13
15.如图14,A,B,C是☉O上的点,且∠ACB=140°.请在这个圆中,仅用无刻度的直尺画出下列度数的圆周角:40°,50°,90°,140°,并说明作法及理由.
图14
答案
1.D
2.C [解析]在△ABC中,∠ABC=71°,∠CAB=53°,∴∠C=180°-71°-53°=56°,
∴∠ADB=∠C=56°.
3.等腰 [解析]∵AB=AC,∴∠ABC=∠C.
∵∠AED=∠ABC,∴∠C=∠AED,
∴DE=CD,∴△CDE是等腰三角形.
4.解:(1)∵AB是☉O的直径,∴∠ADB=90°.
∵∠B=∠ACD=30°,
∴∠BAD=90°-∠B=90°-30°=60°.
(2)∵∠ADB=90°,∠B=30°,∴DB=ADtanB=3AD=3×3=3.
5.C [解析]∵四边形ABCD内接于☉O,∠B=108°,∴∠D=180°-∠B=180°-108°=72°.
6.60 [解析]∵∠BOD=120°,
∴∠A=12∠BOD=60°.
∵四边形ABCD是圆内接四边形,
∴∠A+∠BCD=180°.
又∵∠BCD+∠DCE=180°,
∴∠DCE=∠A=60°.
7.解:∵BC为☉O的直径,∴∠BAC=90°.
又∵∠ACB=20°,
∴∠B=90°-20°=70°.
∵四边形ABCD为☉O的内接四边形,
∴∠B+∠D=180°,∴∠D=110°.
∵D为AC的中点,∴AD=DC,
∴AD=DC,
∴∠DAC=∠DCA=12(180°-∠D)=35°.
8.证明:∵BC=BE,
∴∠E=∠BCE.
∵四边形ABCD是圆内接四边形,
∴∠A+∠DCB=180°.
又∵∠BCE+∠DCB=180°,
∴∠A=∠BCE,
∴∠A=∠E,
∴AD=DE,
∴△ADE是等腰三角形.
9.C [解析]∵圆内接四边形的对角互补,∴∠A∶∠B∶∠C∶∠D=3∶4∶6∶5.设∠A的度数为3x,则∠B,∠C,∠D的度数分别为4x,6x,5x,∴3x+4x+6x+5x=360°,∴x=20°,则∠D=
100°.
10.A [解析]连接BC,如图.∵B(-4,0),C(0,3),∴OB=4,OC=3,∴BC=32+42=5,
∴sin∠OBC=OCBC=35.∵∠CDO=∠OBC,∴sin∠CDO=sin∠OBC=35.
11.二
12.60 [解析]∵四边形OABC是平行四边形,∴∠AOC=∠ABC.设∠D=x,则∠ABC=∠AOC=
2∠D=2x.由∠D+∠ABC=180°可得x+2x=180°,解得x=60°,故∠D=60°.
13.解:(1)∵BC=DC,
∴∠CBD=∠CDB=39°,
∴∠BAC=∠CDB=39°,∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°.
(2)证明:∵EC=BC,∴∠CEB=∠CBE.
∵∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD.
∵BC=DC,∴BC=DC,∴∠BAE=∠CBD,
∴∠1=∠2.
14.解:(1)证明:∵AD平分∠EAC,
∴∠EAD=∠DAC.
∵四边形AFBC内接于圆,
∴∠FBC+∠FAC=180°.
又∵∠DAC+∠FAC=180°,
∴∠DAC=∠FBC.
∵∠EAD=∠FAB=∠FCB,
∴∠FBC=∠FCB,∴FB=FC.
(2)证明:∵∠FAB=∠FCB,∠FCB=∠FBD,∴∠FAB=∠FBD.
又∵∠AFB=∠BFD,
∴△FBA∽△FDB,∴FBFD=FAFB,
∴FB2=FA·FD.
(3)∵AB是圆的直径,
∴∠ACB=∠ACD=90°.
∵∠EAC=120°,
∴∠BAC=180°-∠EAC=60°.
在Rt△ABC中,AB=BCsin∠BAC=6sin60°=43(cm),∠ABC=90°-∠BAC=30°.
在Rt△ADC中,∠DAC=12∠EAC=60°,∴∠D=30°,∴∠ABC=∠D,
∴AD=AB=43cm.
15.解:答案不唯一.如图,∠D=40°,∠BAD=50°,∠ABD=90°,∠AEB=140°.
作法:作直径AD,连接BD,AB,在AB上任取一点E(与点A,B,C不重合),连接AE,BE.
理由:∵∠ACB+∠D=180°,∠ACB=140°,
∴∠D=180°-140°=40°.
∵AD为☉O的直径,∴∠ABD=90°,
∴∠BAD=90°-∠D=50°.
由同弧所对的圆周角相等,可知∠AEB=∠ACB=140°.