数学九年级上册28.3 圆心角和圆周角测试题

这是一份数学九年级上册28.3 圆心角和圆周角测试题，共8页。

知识点 1 圆周角的定义
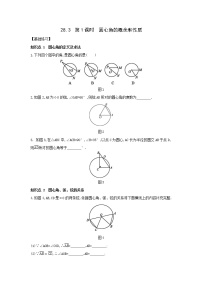
1.下列四个图中,∠α是圆周角的是( )
知识点 2 圆周角定理
2.[2020·柳州] 如图,点A,B,C在☉O上,若∠BOC=70°,则∠A的度数为( )


A.35° B.40° C.55° D.70°
3.如图,AB是☉O的直径,C,D是☉O上的两点,∠AOC=120°,则∠CDB= °.
4.[教材例2变式] 如图,已知☉O是△ABC的外接圆,连接AO.若∠B=50°,则
∠OAC= °.

5.[2020·随州] 如图,点A,B,C在☉O上,AD是∠BAC的平分线,若∠BOC=120°,则∠CAD的度数为 .
6.[2020·绍兴改编] 如图,点A,B,C,D,E均在☉O上,∠BAC=15°,∠CED=30°,则
∠BOD的度数为 .
7.如图1,A,B,P是半径为2的☉O上的三点.若∠APB=45°,则弦AB的长为 .
图1
知识点 3 圆周角定理的推论
8.如图2,BC是☉O的弦,A是圆上一点.
(1)若BC是☉O的直径,则∠A= °;
(2)若∠A=90°,则BC是☉O的 .

图2
9.如图3,BC是☉O的直径,A是☉O上的一点,∠OAC=32°,则∠B的度数是( )
图3
A.58° B.60° C.64° D.68°
10.在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径.如图4,在直角角尺中,∠AOB=90°,将点O放在圆周上,分别确定OA,OB与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )

图4
A.17 B.14 C.12 D.10
11.如图5,AB为☉O的直径,AB=AC,BC交☉O于点D,AC交☉O于点E,∠BAC=50°,求∠EBC的度数.
图5
【能力提升】
12.[2020·鞍山] 如图6,☉O是△ABC的外接圆,半径为2cm.若BC=2cm,则∠A的度数为( )

图6
A.30° B.25° C.15° D.10°
13.如图7,B,C是☉O上的两点,且∠α=96°,A是☉O上的一个动点(不与点B,C重合),则∠A的度数为( )
图7
A.48° B.132° C.48°或132° D.96°
14.[2020·陕西] 如图8,点A,B,C在☉O上,BC∥OA,连接BO并延长,交☉O于点D,连接AC,DC.若∠A=25°,则∠D的大小为( )
图8
A.25° B.30° C.40° D.50°
15.如图9,AB是半圆O的直径,C,D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠D=70°,求∠CAD的度数;
(2)若AC=8,DE=2,求AB的长.
图9
16.如图10,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE.
(1)求证:AC=AE;
(2)求△ACD的外接圆的直径.
图10
答案
1.C [解析]根据圆周角的定义,顶点在圆上,可排除选项D.根据圆周角的定义,两边都与圆相交可排除选项A,B.故选C.
2.A [解析]∵∠BOC=70°,
∴∠A=12∠BOC=35°.
3.30
4.40 [解析]连接CO.∵∠B=50°,∴∠AOC=2∠B=100°.又∵OA=OC,
∴∠OAC=12(180°-100°)=40°.
5.30° [解析]∵∠BAC=12∠BOC=12×120°=60°,而AD是∠BAC的平分线,
∴∠CAD=12∠BAC=30°.
6.90° [解析]∵∠BAC=15°,∠CED=30°,
∴∠BOC=2∠BAC=30°,∠DOC=2∠CED=60°,
∴∠BOD=∠BOC+∠DOC=90°.
7.22 [解析]连接OA,OB.∵∠APB和∠AOB分别是AB所对的圆周角和圆心角,∴∠AOB=
2∠APB=2×45°=90°.在Rt△AOB中,OA=OB=2,∴AB=OA2+OB2=22+22=22.
8.(1)90 (2)直径
9.A [解析]∵OA=OC,∴∠C=∠OAC=32°.
∵BC是☉O的直径,∴∠CAB=90°,∴∠B=90°-32°=58°.
10.C [解析]连接CD.∵∠AOB=90°,∴CD为圆的直径,CD=OC2+OD2≈12.故选C.
11.解:∵AB为☉O的直径,
∴∠AEB=90°,
∴∠ABE=90°-∠BAC=90°-50°=40°.
∵AB=AC,
∴∠ABC=12(180°-∠BAC)=65°,
∴∠EBC=∠ABC-∠ABE=25°.
12.A [解析]如图,连接OB,OC.∵☉O的半径为2cm,BC=2cm,∴OB=OC=BC,∴△OBC为等边三角形,∴∠BOC=60°,∴∠A=12∠BOC=30°.
13.C [解析]当点A在BC上时,∠A=12∠1=12×(360°-96°)=132°;当点A'在BMC上时,连接BA',CA',则∠A'=12∠BOC=12×96°=48°,∴∠A的度数为48°或132°.
14.C [解析]∵BC∥OA,∴∠ACB=∠A=25°,∠B=∠AOB=2∠ACB=50°.∵BD是☉O的直径,
∴∠BCD=90°,∴∠D=90°-∠B=90°-50°=40°.
15.解:(1)∵OA=OD,∠D=70°,
∴∠OAD=∠D=70°,
∴∠AOD=180°-∠OAD-∠D=40°.
∵AB是半圆O的直径,∴∠C=90°.
∵OD∥BC,∴∠B=∠AOD=40°,
∴∠BAC=180°-∠C-∠B=180°-90°-40°=50°,
∴∠CAD=∠OAD-∠BAC=70°-50°=20°.
(2)连接OC.
∵OE∥BC,
∴∠AEO=∠ACB=90°,△AOE∽△ABC,
∴AEAC=AOAB.
∵AO=BO=12AB,∴AEAC=12.
又∵AC=8,∴AE=12AC=4.
设AO=x,则OE=OD-DE=x-2.
∵在Rt△OAE中,OE2+AE2=AO2,
∴(x-2)2+42=x2,解得x=5,∴AO=5,
∴AB=2AO=10.
16.解:(1)证明:∵∠ACB=90°,且∠ACB为圆的圆周角,
∴AD为圆的直径,
∴∠AED=90°,即∠ACB=∠AED.
∵AD是△ABC的角平分线,
∴∠CAD=∠EAD.
又∵AD=AD,
∴△ACD≌△AED,∴AC=AE.
(2)∵△ABC是直角三角形,且AC=6,BC=8,
∴AB=AC2+BC2=62+82=10.
由(1)知∠AED=90°,△ACD≌△AED,
∴CD=DE,∠BED=90°.
∵AC=AE,AC=6,∴AE=6.
设CD=DE=x,则BD=BC-CD=8-x,BE=AB-AE=10-6=4.
在Rt△BED中,根据勾股定理,得
BD2=BE2+DE2,
即(8-x)2=42+x2,解得x=3,∴CD=3.
∵AC=6,△ACD是直角三角形,
∴AD2=AC2+CD2=62+32=45,
∴AD=35.
∵∠ACD=90°,
∴AD为△ACD的外接圆的直径,
即△ACD的外接圆的直径为35.