人教版八年级上册11.1.3 三角形的稳定性教案

这是一份人教版八年级上册11.1.3 三角形的稳定性教案，共6页。教案主要包含了 知识点讲解 ， 例题讲解 ， 变式训练 ， 巩固提高 等内容，欢迎下载使用。

1．三角形的稳定性：
三角形的三边长确定，则三角形的形状就唯一确定，这叫做三角形的稳定性．
注意：（1）三角形具有稳定性；（2）四边形没有稳定性.
2．三角形的内角和定理：三角形的内角和等于180°．
推理过程：
一、作CM∥AB，则∠4=∠1，而∠2+∠3+∠4=1800，
即∠A+∠B+∠ACB=1800．
二、作MN∥BC，则∠2=∠B，∠3=∠C，而∠1+∠2+∠3=1800，
即∠BAC+∠B+∠C=1800．
注意：（1）证明的思路很多，基本思想是组成平角．
（2）应用内角和定理可解决已知二个角求第三个角或已知三角关系求三个角．
（3）特殊三角形的内角关系：直角三角形两锐角互余；等边三角形每个内角都等于600
3．三角形的外角的定义
三角形一边与另一边的延长线组成的角，叫做三角形的外角.
注意：每个顶点处都有两个外角，但这两个外角是对顶角.
如:∠ACD、∠BCE都是△ABC的外角，且∠ACD=∠BCE.
所以说一个三角形有六个外角，但我们每个一个顶点处
只选一个外角，这样三角形的外角就只有三个了.
4．三角形外角的性质
（1） 三角形的一个外角等于与它不相邻的两个内角之和．
（2） 三角形的一个外角大于与它不相邻的任何一个内角．
注意：（1）它不相邻的内角不容忽视；
（2）作CM∥AB由于B、C、D共线
∴∠A=∠1，∠B=∠2. 即∠ACD=∠1+∠2=∠A+∠B.
那么∠ACD>∠A.∠ACD>∠B.
【 例题讲解 】
1.如图，工人师傅砌门时，常用木条EF固定矩形门框ABCD，使其不变形，这种做法的根据是（ ）
A．两点之间线段最短 B．矩形的对称性
C．矩形的四个角都是直角 D．三角形的稳定性

2.王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（ ）
A．0根 B．1根 C．2根 D．3根

3. 在一个三角形中，下列说法错误的是( )．
A．可以有一个锐角和一个钝角
B．可以有两个锐角
C．可以有一个锐角和一个直角
D．可以有两个钝角
4. 已知一个三角形三个内角度数的比是1∶5∶6，则其最大内角的度数为( )．
A．60° B．75° C．90° D．120°
5. 如图所示，∠1为三角形的外角的是( )．
【 变式训练 】
1.下列图中具有稳定性的是（ ）

A． B． C． D．
2.在生活中，我们常常会看到如图所示的情况，在电线杆上拉两根钢筋来加固电线杆，这样做的依据是 .

3. 若一个三角形三个内角度数的比为2∶3∶4，那么这个三角形是( )．
A．直角三角形 B．锐角三角形
C．钝角三角形 D．等边三角形
4. △ABC中，若∠B＝∠A＋∠C，则△ABC是__________三角形．
5.如图，△ABC中，∠A＝70°，∠B＝60°，点D在BC的延长线上，则∠ACD等于( )．
A．100° B．120°
C．130° D．150°
6. 如图，∠1，∠2，∠3的大小关系为( )．

A．∠2＞∠1＞∠3B．∠1＞∠3＞∠2
C．∠3＞∠2＞∠1D．∠1＞∠2＞∠3
7.如图，将一副三角板按图示的方法叠在一起，则图中∠α等于________．

8.如图，已知△ABC中，∠B＝65°，∠C＝45°，AD是BC边上的高，AE是∠BAC的平分线，求∠DAE的度数．

【 巩固提高 】
1.人站在晃动的公共汽车上．若你分开两腿站立，则需伸出一只手去抓栏杆才能站稳，这是利用了 .
2．如图，是边长为25cm的活动四边形衣帽架，它应用了四边形的 ．

教案
教 师:
初 学生:
上课时间
年 月 日
阶 段:
基础（ √） 提高（ ） 强化（ ）
课时计划
共 次课 第 次课
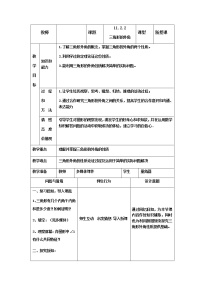
教学课题:
三角形的稳定性、三角形的内外角
教学目标:
理解三角形的稳定性
学会推导三角形内角和与外交和
教学重难点：
重点：三角形的稳定性与三角形的内角和定理
难点：三角形的内角和定理