
初中人教版第十一章 三角形数学活动 镶嵌教学设计
展开一、教学目标
(一)学习目标
1.理解平面镶嵌的含义
2.掌握多边形单独镶嵌的条件
3.掌握多边形组合镶嵌的条件
(二)学习重点
掌握平面镶嵌的定义,以及平面镶嵌的条件
(三)学习难点
多边形单独镶嵌与组合镶嵌的条件
二、教学设计
(一)课前设计
1.预习任务
用一些 不重叠摆放 的多边形把平面的一部分 完全覆盖 ,叫做多边形覆盖平面(或平面镶嵌).
2.预习自测
(1)平面镶嵌的条件是:拼接在同一个顶点处的各个多边形的内角之和等于_________.
【知识点】平面镶嵌(密铺)
【思路点拨】根据平面镶嵌的概念进行分析
【答案】360°
(2)下列图形不能用来铺满地面的是( ).
A.钝角三角形 B.正方形 C.梯形 D.正五边形
【知识点】平面镶嵌(密铺)
【思路点拨】根据平面镶嵌的概念进行分析
【解题过程】A.钝角三角形的3个内角和为180°,可以构成一个平角,6个内角可以在一个顶点处构成一个周角,因此正确.
B.正方形的每个内角都等于90°,4个内角和为360°,4个内角在一个顶点处构成一个周角,因此正确.
C.梯形的4个内角和为360°,可以够成一个周角,4个内角在一个顶点处构成一个周角,因此正确.
D.正五边形的每个内角都等于108°,360°不是108°的整数倍,也就是用一些108°的角不能拼出360°的角,因此错误.
【答案】D
(二)课堂设计
1.知识回顾
(1)正三角形的一个内角度数为 60° ,正方形的一个内角度数为 90° ,正五边形的一个内角度数为 108° ,正六边形的一个内角度数为 120° ,正八边形的一个内角度数为 135° ,正十二边形的一个内角度数为 150° .
(2)三角形的内角和为 180° ,四边形的内角和为 360° ,n边形的内角和 (n-2)×180°.
2.问题探究
探究一 探究平面镶嵌的含义
●活动1 回顾旧知,回忆正多边形的每个内角度数
学生活动:60°,90°,108°,120°,135°,150°
【设计意图】通过对旧知识的回顾,为新知识的学习作铺垫
● 活动2 整合旧知,探究平面镶嵌的概念
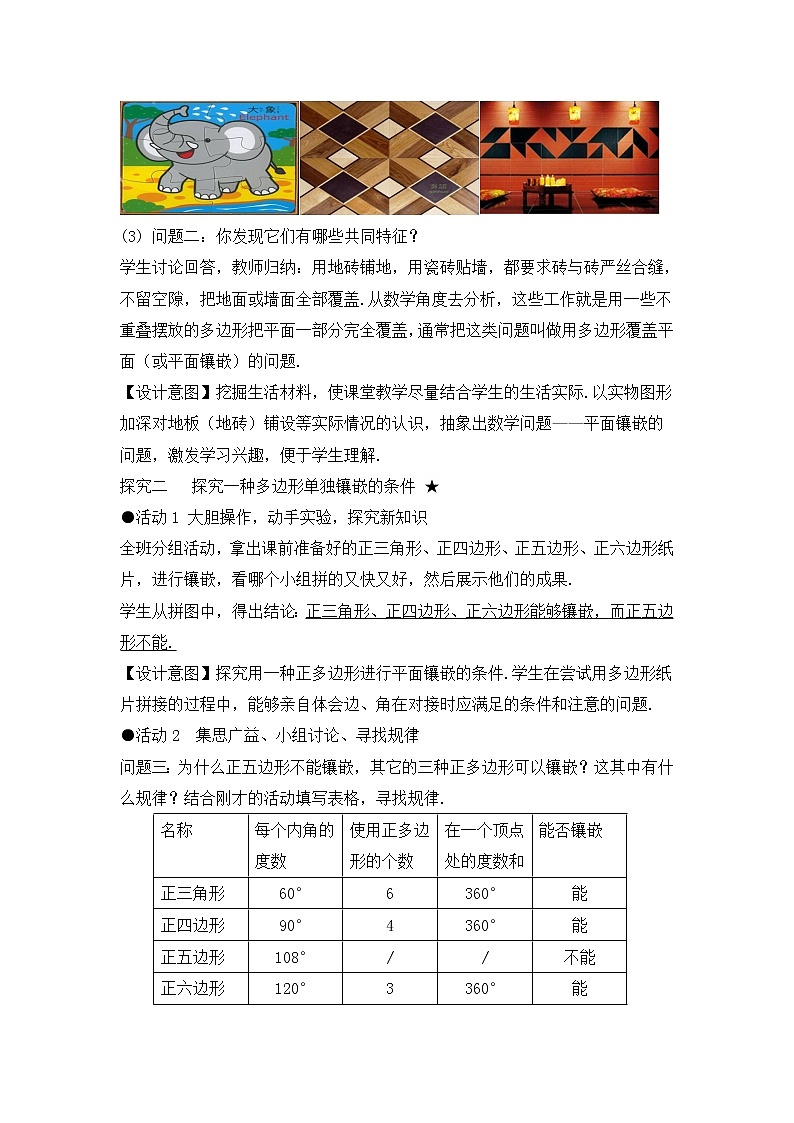
(1)问题一:回想你家客厅(卧室)里的地砖、地板铺设情况,并说说是用什么形状的地砖、地板铺成的?
(2)展示实物:拼图图片和生活中瓷砖的图片
(3) 问题二:你发现它们有哪些共同特征?
学生讨论回答,教师归纳:用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖.从数学角度去分析,这些工作就是用一些不重叠摆放的多边形把平面一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
【设计意图】挖掘生活材料,使课堂教学尽量结合学生的生活实际.以实物图形加深对地板(地砖)铺设等实际情况的认识,抽象出数学问题——平面镶嵌的问题,激发学习兴趣,便于学生理解.
探究二 探究一种多边形单独镶嵌的条件 ★
●活动1 大胆操作,动手实验,探究新知识
全班分组活动,拿出课前准备好的正三角形、正四边形、正五边形、正六边形纸片,进行镶嵌,看哪个小组拼的又快又好,然后展示他们的成果.
学生从拼图中,得出结论:正三角形、正四边形、正六边形能够镶嵌,而正五边形不能.
【设计意图】探究用一种正多边形进行平面镶嵌的条件.学生在尝试用多边形纸片拼接的过程中,能够亲自体会边、角在对接时应满足的条件和注意的问题.
●活动2 集思广益、小组讨论、寻找规律
问题三:为什么正五边形不能镶嵌,其它的三种正多边形可以镶嵌?这其中有什么规律?结合刚才的活动填写表格,寻找规律.
小组讨论,你组发现的规律:如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍).
【设计意图】通过以上环节,学生在实验过程中充分体验数据的收集和分析给学习带来的帮助和启发,逐渐发现用一种正多边形能够镶嵌的规律.
●活动3 反思过程,小组交流,得出结论
分析表格可得到:正三角形、正四边形、正六边形的内角度数分别是60°,90°,120°,它们都是360°的约数,说明在一个顶点处有整数个这样的正多边形镶嵌;而正五边形的内角为108°,108°不是360°的约数,在一个顶点处没有整数个正五边形镶嵌成一个平面图案. 从拼图中,可得出正三角形、正四边形、正六边形能够镶嵌,而正五边形不能.
结论:在用同一种正多边形进行覆盖时,关键是看正多边形的一个内角,当周角360°是一个内角的整数倍时,即一个内角的正整数倍是360°时,这种正多边形可以覆盖平面,否则不可以.即:如果一个正多边形可以进行镶嵌,那么内角一定是360°的约数(或360°一定是这个多边形内角的整数倍).
【设计意图】这一问题学生独立回答,比较困难,因此这里采取小组合作,教师指导的教学方法.学生在合作中学习与人交流,通过交流,学生可以用自己的语言清楚地解释这一问题,同时也提高了自己的语言表达能力.
●活动4 拓展延伸,探究用一种任意多边形进行平面镶嵌的条件
问题四:任意剪出一些形状、大小相同的三角形纸板,小组合作拼拼看,它们能否镶嵌成平面图案.
任意剪出一些形状、大小相同的四边形纸板,小组合作拼拼看,它们能否镶嵌成平面图案.
学生活动:形状、大小完全相同的任意三角形可以进行镶嵌.形状、大小完全相同的任意四边形可以进行镶嵌.
问题五:用一些形状、大小相同的多边形,它们能够镶嵌成平面图案的条件是什么?小组交流
总结:用一些形状、大小相同的多边形,它们能够镶嵌成平面图案的条件:对于给定的某种正多边形,它能否拼成一个平面图形,而不留一点空隙.显然问题的关键在于分析能用于完整铺平地面的正多边形的内角特点.当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角360°时,就铺成一个平面图形.
【设计意图】培养学生的操作能力,了解一般的三角形或四边形可以进行平面镶嵌.
探究三 探究用两种正多边形平面镶嵌的条件 ★▲
●活动1 大胆操作,动手实验,发散思维
问题六:用刚才的边长相同的正三角形、正方形、正五边形、正六边形中的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
要求:大家先根据镶嵌的条件动手算一算,拼一拼,填一填,然后小组活动:哪两种正多边形能够镶嵌?看谁找得多?
【设计意图】通过比赛激发学生继续动手实验的欲望,以小组活动进行验证在学生分析时,引导他们依照刚才的表格去收集数据,分析数据通过以上环节,学生在实验过程中充分体验数据的收集和分析给学习带来的帮助和启发,逐渐发现用两种正多边形能够镶嵌的规律.
●活动2 集思广益 ,规律总结
用两种边长相等的正多边形覆盖平面时的条件是:设两种正多边形的内角分别是α、β,当mα+nβ=360°中的m,n有正整数满足时,这两种正多边形可以覆盖平面.
【数学思想】方程思想,模型思想
3. 课堂总结
知识梳理:
(1)用一些不重叠摆放的多边形把平面一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)的问题.
(2)用同一种正多边形平面镶嵌的条件是:当正多边形的一个内角的正整数倍是360°时,这种正多边形可以覆盖平面.
(3)在一般的多边形中,只有三角形、四边形可以平面覆盖,因为三角形和四边形的内角和的正整数倍是360°.
(4)用两种边长相等的正多边形覆盖平面时的条件是:设两种正多边形的内角分别是a,β当ma+nβ=360°中的m,n有正整数满足时,这两种正多边形可以覆盖平面.
重难点归纳:
(1)平面镶嵌是用一种或几种平面图形进行拼接,要求图形与图形之间不留空隙、不重叠地铺成一片.
(2)平面镶嵌的条件是:
①拼接在同一点的各个角的和恰好等于360°.
②相邻的多边形有公共边.
(三)课后作业
基础型 自主突破
1.用多边形把平面的一部分完全覆盖的意思是指既不留______,又不_____,这与多边形的_______有关.
【知识点】平面镶嵌(密铺)
【思路点拨】根据平面镶嵌的概念进行分析
【答案】一丝空隙 互相重叠 内角
2.我们已经知道,用一种正多边形铺地面时,只有______,_______,_______三种图形能铺满地面.
【知识点】平面镶嵌(密铺)
【思路点拨】根据用一种正多边形平面镶嵌的条件进行分析
【答案】正三角形 正方形 正六边形
3.下列图形中,能镶嵌成平面图案的是( )
A.正五边形 B.正六边形 C.正七边形 D.正八边形
【知识点】平面镶嵌(密铺)
【思路点拨】根据用一种正多边形平面镶嵌的条件进行分析
【解题过程】
A.正五边形的每一个内角的度数为108°,不能被360°整除,所以不能镶嵌
B.正六边形的每一个内角的度数为120°,能被360°整除,所以能镶嵌
C.正七边形的每一个内角的度数约为129°,不能被360°整除,所以不能镶嵌
D.正八边形的每一个内角的度数为135°,不能被360°整除,所以不能镶嵌
【答案】B
4.下列正多边形的组合中 , 不能镶嵌的是 ( )
A . 正方形和正三角形 B. 正方形和正八边形
C. 正三角形和正十二边形 D. 正三角形和正五边形
【知识点】平面镶嵌(密铺)
【数学思想】方程思想,模型思想
【思路点拨】根据用两种正多边形平面镶嵌的条件进行分析
【解题过程】
A. 90°×2+60°×3=360°能镶嵌
B. 90°×1+135°×2=360°能镶嵌
C.60°×1+150°×2=360°能镶嵌
D.60°×m+108°×n=360° m,n取不到整数,不能镶嵌
【答案】D
5.有以下边长相等的三种图形:①正三角形②正方形③正八边形.选其中两种图形镶嵌成平面图形,请你写出两种不同的选法:_______或________.(用序号表示图形)
【知识点】平面镶嵌(密铺)
【数学思想】方程思想,模型思想
【思路点拨】根据用两种正多边形平面镶嵌的条件进行分析
【解题过程】①和②:60°×3+90°×2=360° 能镶嵌
①和③:60°×m+135°×n=360° m,n取不到整数,不能镶嵌
②和③:90°×1+135°×2=360°能镶嵌
【答案】①和②,②和③
6.用正三角形和正十二边形镶嵌,可能情况有( )
A.1种 B.2种 C.3种 D.4种
【知识点】平面镶嵌(密铺)
【数学思想】方程思想,模型思想
【思路点拨】根据用两种正多边形平面镶嵌的条件进行分析
【解题过程】60°×1+150°×2=360°仅这一种情况
【答案】 A
能力型 师生共研
7.如果只用一种正多边形作平面镶嵌,而且在每一个正多边形的每一个顶点周围都有4个正多边形,则该正多边形的内角度数为( )
A.120° B.90° C.60° D.45°
【知识点】平面镶嵌(密铺)
【思路点拨】根据用一种多边形平面镶嵌的条件进行分析
【解题过程】因为拼接在同一个顶点处的各个多边形的内角之和等于360°,所以360°÷4=90°
【答案】B
8.用正三角形和正方形镶嵌,若每一个顶点周围有m个正三角形、n 个正六边形,则m,n满足的关系式是( )
A. 2m+3n=12 B. m+n=8 C. 2m+n=6 D. m+2n=6
【知识点】平面镶嵌(密铺)
【数学思想】方程思想,模型思想
【思路点拨】根据用两种多边形平面镶嵌的条件进行分析
【解题过程】60°×m+90°×n=360°得2m+3n=12
【答案】A
9.用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并填空:当黑色瓷砖为20块时,白色瓷砖为( )块;当白色瓷砖为n2(n为正整数)块时,黑色瓷砖为( )块
【数学思想】方程思想
【思路点拨】寻找数字间的规律并运用这一规律解决问题.
【解题过程】:第n个图形有n2块白瓷砖,瓷砖的总数是(n+2)2,则黑瓷砖有(n+2)2-n2=4n+4块;
那么当黑色瓷砖为20块时,(n+2)2-n2=20,计算得出n=4,那么白瓷砖为42=16.
【答案】16,4n+4
10.当围绕一个顶点拼在一起的多边形中有_____个正三角形与______个正方形,这个组合能铺满平台;当围绕一个顶点拼在一起的多边形中有______个正三角形与_______个正方形和______个正六边形,则这个组合也能平面镶嵌.
【知识点】平面镶嵌(密铺)
【思路点拨】根据用两种多边形平面镶嵌的条件进行分析
【解题过程】(1)60°×3+ 90°×2=360°
(2)60°×1+90°×2+120°×1=360°
【答案】3,2 ,1,2,1
自助餐
1.下列正多边形不能够镶嵌成平面图案的是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
【知识点】平面镶嵌(密铺)
【数学思想】方程思想
【思路点拨】根据用一种正多边形平面镶嵌的条件进行分析
【解题过程】
A.60°×6=360°能镶嵌
B.90°×4=360°能镶嵌
C.108°×3=324°,108°×4=432°不能镶嵌
D.120°×3=360°能镶嵌
【答案】C
2.用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的正方形的个数是( )
A.3 B.4 C.5 D.6
【知识点】平面镶嵌(密铺)
【思路点拨】根据用一种正多边形平面镶嵌的条件进行分析
【解题过程】90°×4=360°
【答案】B
3.用两种正多边形进行镶嵌,不能与正三角形匹配的多边形是( )
A.正方形 B.正六边形 C.正十二边形 D.正十八边形
【知识点】平面镶嵌(密铺)
【思路点拨】根据用两种多边形平面镶嵌的条件进行分析
【解题过程】60°+160°×2=380°
【答案】D
4.下列说法正确的是( )
A.只有正多边形可以平面镶嵌 B最多能用两种正多边形进行平面镶嵌 C.一般的凸多边形也可以平面镶嵌 D.只有正五边形不可以平面镶嵌
【知识点】平面镶嵌(密铺)
【思路点拨】根据用平面镶嵌的条件进行分析
【解题过程】任何一个凸四边形的内角和都是360°
【答案】C
5.某商店出售下列五种形状的地砖:⑴等腰三角形、⑵四边形、⑶正五边形、⑷正六边形、⑸正八边形,如果只选用其中一种地砖镶嵌地面,可供选择的地砖共有 种。
【知识点】平面镶嵌(密铺)
【数学思想】方程思想,模型思想
【思路点拨】根据用平面镶嵌的条件进行分析
【解题过程】⑴任意三角形的内角和都180°,放在同一顶点处6个三角形就可以镶嵌;⑵任意四边形的内角和都360°,放在同一顶点处4四边形就可以镶嵌;⑶正五边形的一个内角是108°,不能被360°整除;⑷正六边形的一个内角是120°,能被360°整除;⑸正八边形的一个内角是135°,不能被360整除;
【答案】⑴⑵⑷
6.请你用正三角形、正方形、正六边形三种图形设计一个能铺满整个地面的美丽图案(教学说明:开放性作业可以扩展学生的想象力和动手操作的能力)
数学视野:漫谈镶嵌
1619年,数学家奇(J.Kepler)第一个利用正多边形密铺平面.
1891年,苏联物理学家弗德洛夫()发现了十七种不同的平面密铺的对称图案.
1924年,数学家波利亚(Plya)和尼格利(Nigeli)重新发现这个事实。1936年荷兰艺术家埃舍尔()偶然到西班牙的格兰拿大旅行,在参观建于十四世纪的阿罕伯拉宫时,发现宫内的地板、天花板和墙壁满是密铺图案的装饰.他因而得到启发,创造了无数的艺术作品,给人留下深刻印象,更让人对数学有了新的认识.
1936年,版画家埃舍尔旅行到了西班牙并且在Alhambra看到了当地使用的瓦的图案.激发了他对图形镶嵌的兴趣,他被每种镶嵌图形迷住了,不论是常规的还是不规则的; 并且对一种他称为变形的形状特别感兴趣,这其中的图形相互变化影响,并且有时突破平面的自由。那年他花了好几天勾画这些瓦面,过后宣称这些 "是我所遇到的最丰富的灵感资源",1957年他写了一篇关于镶嵌图形的文章,其中评论道:"在数学领域,规则的平面分割已从理论上研究过了...,难道这意味着它只是一个严格的数学的问题吗?按照我的意见,.数学家们打开了通向一个广阔领域的大门,但是他们自己却从未进入门后面的花园.埃舍尔在他的镶嵌图形中利用了这些基本的图案,用几何学中的反射、平滑反射、变换和旋转来获得更多的变化图案.精心地使这些基本图案扭曲变形为动物、鸟和其他的形状.这样的改变效果造就了平面镶嵌成为数学与艺术的完美组合!
正多边形的每个内角度数
正三角形
正六边形
正四边形
正八边形
正五边形
正十二边形
名称
每个内角的度数
使用正多边形的个数
在一个顶点处的度数和
能否镶嵌
正三角形
60°
6
360°
能
正四边形
90°
4
360°
能
正五边形
108°
/
/
不能
正六边形
120°
3
360°
能
序号
方案选择
是否可以镶嵌
每个内角的度数
同一个顶点使用个数
1
正三角形
是
60°
3
正方形
90°
2
2
正三角形
否
/
/
正五边形
/
/
3
正三角形
是
60°
2或4
正六边形
120°
2或1
4
正方形
否
/
/
正五边形
/
/
5
正方形
否
/
/
正六边形
/
/
6
正五边形
否
/
/
正六边形
/
/
初中数学北师大版八年级下册1 图形的平移教案: 这是一份初中数学北师大版八年级下册1 图形的平移教案,共5页。教案主要包含了教材分析,教学目标,教学重点,学情分析,教法与学法,教学过程,板书设计等内容,欢迎下载使用。
人教版八年级上册第十四章 整式的乘法与因式分解综合与测试教案: 这是一份人教版八年级上册第十四章 整式的乘法与因式分解综合与测试教案,共3页。教案主要包含了目标和目标解析,教学问题诊断分析等内容,欢迎下载使用。
人教版八年级上册第十二章 全等三角形数学活动教案: 这是一份人教版八年级上册第十二章 全等三角形数学活动教案,共3页。教案主要包含了内容和内容解析,目标和目标解析,教学问题诊断分析,教学过程设计等内容,欢迎下载使用。













