2022高考物理一轮复习学案 007重力场中的等时圆模型 精讲精练

这是一份2022高考物理一轮复习学案 007重力场中的等时圆模型 精讲精练，共7页。

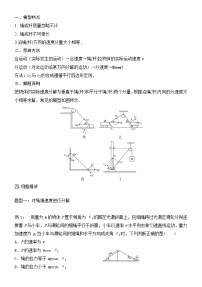
如图甲、乙所示，质点沿竖直面内圆环上的任意一条光滑弦从上端由静止滑到底端，可知加速度a＝gsinθ，位移x＝2Rsinθ，由匀加速直线运动规律有x＝eq \f(1,2)at2，得下滑时间t＝2eq \r(\f(R,g))，即沿竖直直径自由下落的时间。图丙是甲、乙两图的组合，不难证明有相同的结论。
2．结论
模型1 质点从竖直面内的圆环上沿不同的光滑弦上端由静止开始滑到环的最低点所用时间相等，如图甲所示；
模型2 质点从竖直面内的圆环上最高点沿不同的光滑弦由静止开始滑到下端所用时间相等，如图乙所示；
模型3 两个竖直面内的圆环相切且两环的竖直直径均过切点，质点沿不同的光滑弦上端由静止开始经切点滑到下端所用时间相等，如图丙所示。
3．思维模板
其中模型3可以看成两个等时圆，分段按上述模板进行时间比较。
二.例题精讲
例1：如图所示，位于竖直平面内的固定光滑圆环轨道与水平面相切于M点，与竖直墙相切于A点。竖直墙上另一点B与M的连线和水平面的夹角为60°，C是圆环轨道的圆心。已知在同一时刻a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点；c球由C点自由下落到M点。则( )
A．a球最先到达M点
B．b球最先到达M点
C．c球最先到达M点
D．b球和c球都可能最先到达M点
解析 由等时圆模型知，a球运动时间小于b球运动时间，a球运动时间和沿过CM的直径的下落时间相等，所以从C点自由下落到M点的c球运动时间最短，故C正确。
答案 C
例2.如图所示，在同一竖直平面内，从定点P到固定斜面(倾角为θ)搭建一条光滑轨道PM，使物体从P点释放后，沿轨道下滑到斜面的时间最短，则此轨道与竖直线的夹角α为多少？
M
•P
θ
α
解析：先用解析法求解。从定点P向斜面作垂线，垂足为D，如图1所示，设P到斜面距离为h，则轨道长度为
M
•P
θ
α
图1
D
h
物体沿轨道下滑的加速度
由于
联立解得：
令根式中分母，利用积化和差得：
，θ一定，当时，分母y取得最大值，物体沿轨道下滑的时间t最小。
图2
θ
•P
α1
M1
M2
α2
α
•P
M2
θ
θ
甲
乙
再用“等时圆”作图求解。以 α
定点P为“等时圆”最高点，作出系列半径r不同（动态的）“等时圆”，所有轨道的末端均落在对应的“等时圆”圆周上，如图9中甲所示，则轨道长度均可表示为
物体沿轨道下滑的加速度
由于，故得：，
欲t最小，则须“等时圆”的半径r最小。显然，半径最小的“等时圆”在图中与斜面相切于M2点，如图9中乙所示。再根据几何关系可知：。
在这里，用了转化的思想，把求最短时间转化为求作半径最小的“等时圆”，避免了用解析法求解的复杂计算。
三.举一反三，巩固练习
1：如图所示，AB和CD为两条光滑斜槽，它们各自的两个端点均分别位于半径为R和r的两个相切的圆上，且斜槽都通过切点P。设有一重物先后沿两个斜槽，从静止出发，由A滑到B和由C滑到D，所用的时间分别为t1和t2，则t1与t2之比为 ( )
A．2︰1 B．1︰1
C．eq \r(3)︰1D．1︰eq \r(3)
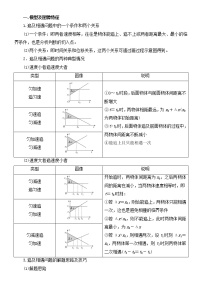
2：如图所示，几条足够长的光滑直轨道与水平面成不同角度，从P点以大小不同的初速度沿各轨道发射小球，若各小球恰好在相同的时间内到达各自的最高点，则各小球最高点的位置 ( )
A．在同一水平线上B．在同一竖直线上
C．在同一抛物线上D．在同一圆周上
3．身体素质拓展训练中，人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看成质点)，若木板的倾斜角不同，人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3，若已知AB、AC、AD与板的夹角分别为70°、90°和105°，则 ( )
A．t1>t2>t3
B．t1C．t1＝t2＝t3
D．不能确定t1、t2、t3之间的关系
4. （2004年高考试题）如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点。每根杆上都套有一个小滑环（图中未画出），三个滑环分别从a、b、c处释放（初速为0），用t1、t2、t3依次表示各滑环到达d所用的时间，则（）
A.t1t2>t3 C.t3>t1>t2 D.t1=t2=t3
图3
5：如图，在设计三角形的屋顶时，为了使雨水能尽快地从屋顶流下，并认为雨水是从静止开始由屋顶无摩擦地流动。试分析和解：在屋顶宽度（2L）一定的条件下，屋顶的倾角应该多大？雨水流下的最短时间是多少？
A
O
B
C
30°
6.倾角为30°的长斜坡上有C、O、B三点，CO = OB = 10m，在C点竖直地固定一长10 m的直杆AO。A端与C点间和坡底B点间各连有一光滑的钢绳，且各穿有一钢球（视为质点），将两球从A点由静止开始、同时分别沿两钢绳滑到钢绳末端，如图1所示，则小球在钢绳上滑行的时间tAC和tAB分别为（取g = 10m/s2）
A．2s和2s B． 和 2s
C．和4s D．4s 和
四.举一反三，巩固练习参考答案
1：如图所示，AB和CD为两条光滑斜槽，它们各自的两个端点均分别位于半径为R和r的两个相切的圆上，且斜槽都通过切点P。设有一重物先后沿两个斜槽，从静止出发，由A滑到B和由C滑到D，所用的时间分别为t1和t2，则t1与t2之比为 ( )
A．2︰1 B．1︰1
C．eq \r(3)︰1D．1︰eq \r(3)
[解析] 设光滑斜槽轨道与水平面的夹角为θ，则物体下滑时的加速度为a＝gsinθ，由几何关系，斜槽轨道的长度s＝2(R＋r)sinθ，由运动学公式s＝eq \f(1,2)at2，得t＝eq \r(\f(2s,a))＝eq \r(\f(2×2R＋rsinθ,gsinθ))＝2eq \r(\f(R＋r,g))，即所用的时间t与倾角θ无关，所以t1＝t2，B项正确。
答案 B
2：如图所示，几条足够长的光滑直轨道与水平面成不同角度，从P点以大小不同的初速度沿各轨道发射小球，若各小球恰好在相同的时间内到达各自的最高点，则各小球最高点的位置 ( )
A．在同一水平线上B．在同一竖直线上
C．在同一抛物线上D．在同一圆周上
[解析] 设某一直轨道与水平面成θ角，末速度为零的匀减速直线运动可逆向看成初速度为零的匀加速直线运动，则小球在直轨道上运动的加速度a＝eq \f(mgsinθ,m)＝gsinθ，由位移公式得l＝eq \f(1,2)at2＝eq \f(1,2)gsinθ·t2，即eq \f(l,sinθ)＝eq \f(1,2)gt2，不同的倾角θ对应不同的位移l，但eq \f(l,sinθ)相同，即各小球最高点的位置在直径为eq \f(1,2)gt2的圆周上，选项D正确。
答案 D
3．身体素质拓展训练中，人从竖直墙壁的顶点A沿光滑杆自由下滑到倾斜的木板上(人可看成质点)，若木板的倾斜角不同，人沿着三条不同路径AB、AC、AD滑到木板上的时间分别为t1、t2、t3，若已知AB、AC、AD与板的夹角分别为70°、90°和105°，则 ( )
A．t1>t2>t3
B．t1C．t1＝t2＝t3
D．不能确定t1、t2、t3之间的关系
[解析] 以AO为直径作圆，可知圆周过C点，B点在圆周外，D点在圆周内。从圆周的最高点沿光滑斜面由静止释放，滑至圆周的时间相等，可以判断t1>t2>t3，A正确。
易错分析：解题能力方面忽略了知识的迁移，遇到此类题，没有想到使用“等时圆”模型，解题时无处下手，导致错选。
答案 A
4. （2004年高考试题）如图所示，ad、bd、cd是竖直面内三根固定的光滑细杆，a、b、c、d位于同一圆周上，a点为圆周的最高点，d点为最低点。每根杆上都套有一个小滑环（图中未画出），三个滑环分别从a、b、c处释放（初速为0），用t1、t2、t3依次表示各滑环到达d所用的时间，则（）
A.t1t2>t3 C.t3>t1>t2 D.t1=t2=t3
解析：选任一杆上的环为研究对象，受力分析并建立坐标如图所示，设圆半径为R，由牛顿第二定律得，
①
再由几何关系，细杆长度 ②
图1
x
y
mg
θ
设下滑时间为，则 ③
由以上三式得， 可见下4滑时间与细杆倾角无关，所以D正确。
5：如图，在设计三角形的屋顶时，为了使雨水能尽快地从屋顶流下，并认为雨水是从静止开始由屋顶无摩擦地流动。试分析和解：在屋顶宽度（2L）一定的条件下，屋顶的倾角应该多大？雨水流下的最短时间是多少？
【解析】：如图4所示，通过屋顶作垂线AC与水平线BD相垂直；并以L为半径、O为圆心画一个圆与AC、BC相切。然后，画倾角不同的屋顶、、…
从图可以看出：在不同倾角的屋顶中，只有是圆的弦，而其余均为圆的割线。根据“等时圆”规律，雨水沿运动的时间最短，且最短时间为
而屋顶的倾角则为
A
O
B
C
30°
6.倾角为30°的长斜坡上有C、O、B三点，CO = OB = 10m，在C点竖直地固定一长10 m的直杆AO。A端与C点间和坡底B点间各连有一光滑的钢绳，且各穿有一钢球（视为质点），将两球从A点由静止开始、同时分别沿两钢绳滑到钢绳末端，如图1所示，则小球在钢绳上滑行的时间tAC和tAB分别为（取g = 10m/s2）
A．2s和2s B． 和 2s
C．和4s D．4s 和
图2
A
O
B
C
30°
α1
α2
D
解析：由于CO = OB =OA ，故A、B、C三点共圆，O为圆心。又因直杆AO竖直，A点是该圆的最高点，如图2所示。两球由静止释放，且光滑无摩擦，满足“等时圆”条件。设钢绳AB和AC与竖直方向夹角分别为α1、α2，该圆半径为r，则对钢球均有
解得：, 钢球滑到斜坡时间t跟钢绳与竖直方向夹角α无关，且都等于由A到D的自由落体运动时间。代入数值得t=2s，选项A正确。