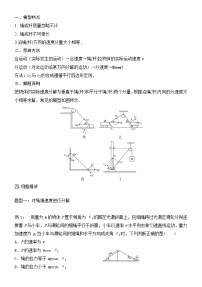
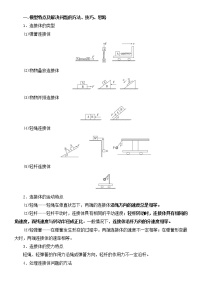
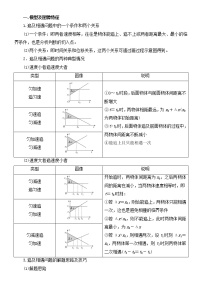
2022高考物理一轮复习学案 018多体平抛运动模型 精讲精练

这是一份2022高考物理一轮复习学案 018多体平抛运动模型 精讲精练，共13页。

2．性质：平抛运动是加速度为g的匀变速曲线运动，运动轨迹是抛物线．
3．研究方法：运动的合成与分解
(1)水平方向：匀速直线运动；
(2)竖直方向：自由落体运动．
4. 平抛运动基本规律
如图1，以抛出点O为坐标原点，以初速度v0方向(水平方向)为x轴正方向，竖直向下为y轴正方向．
图1
(1)位移关系
(2)速度关系
（3）飞行时间
由t＝eq \r(\f(2h,g))知，时间取决于下落高度h，与初速度v0无关．
（4）水平射程
x＝v0t＝v0eq \r(\f(2h,g))，即水平射程由初速度v0和下落高度h共同决定，与其他因素无关．
（5）落地速度
v＝eq \r(v\\al(x2,)＋v\\al(y2,))＝eq \r(v\\al(02,)＋2gh)，以θ表示落地速度与水平正方向的夹角，有tan θ＝eq \f(vy,vx)＝eq \f(\r(2gh),v0)，落地速度与初速度v0和下落高度h有关．
（6）速度改变量
因为平抛运动的加速度为恒定的重力加速度g，所以做平抛运动的物体在任意相等时间间隔Δt内的速度改变量Δv＝gΔt是相同的，方向恒为竖直向下，如图4所示．
图4
（7）两个重要推论
①做平抛运动的物体在任意时刻的瞬时速度的反向延长线一定通过此时水平位移的中点，如图5所示，即xB＝eq \f(xA,2).
图5
推导：
eq \b\lc\ \rc\}(\a\vs4\al\c1(tan θ＝\f(yA,xA－xB),tan θ＝\f(vy,v0)＝\f(2yA,xA)))→xB＝eq \f(xA,2)
②做平抛运动的物体在任意时刻任意位置处，有tan θ＝2tan α.
推导：
eq \b\lc\ \rc\}(\a\vs4\al\c1(tan θ＝\f(vy,v0)＝\f(gt,v0),tan α＝\f(y,x)＝\f(gt,2v0)))→tan θ＝2tan α
5.多体平抛模型
（1）模型特点：涉及到两个或两个以上物体做平抛运动的模型
（2）模型运动规律
①若两物体同时从同一高度(或同一点)抛出，则两物体始终在同一高度，二者间距只取决于两物体的水平分运动。
②若两物体同时从不同高度抛出，则两物体高度差始终与抛出点高度差相同，二者间距由两物体的水平分运动和竖直高度差决定。
③若两物体从同一点先后抛出，两物体竖直高度差随时间均匀增大，二者间距取决于两物体的水平分运动和竖直分运动。
④两条平抛运动轨迹的相交处是两物体的可能相遇处，两物体要在此处相遇，必须同时到达此处。
二.典型例题精讲
题型一：同位置不同速平抛
例1：(2017·全国卷Ⅰ·15)发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)．速度较大的球越过球网，速度较小的球没有越过球网．其原因是( )
A．速度较小的球下降相同距离所用的时间较多
B．速度较小的球在下降相同距离时在竖直方向上的速度较大
C．速度较大的球通过同一水平距离所用的时间较少
D．速度较大的球在相同时间间隔内下降的距离较大
答案 C
解析 由题意知，两个乒乓球均做平抛运动，则根据h＝eq \f(1,2)gt2及veq \\al(y2,)＝2gh可知，乒乓球的运动时间、下降的高度及竖直方向速度的大小均与水平速度大小无关，故选项A、B、D均错误；由发出点到球网的水平位移相同时，速度较大的球运动时间短，在竖直方向下落的距离较小，可以越过球网，故C正确．
题型二：同高不同位置平抛
例2：如图所示，将一小球从水平面MN上方A点以初速度v1向右水平抛出，经过时间t1打在前方竖直墙壁上的P点，若将小球从与A点等高的B点以初速度v2向右水平抛出，经过时间t2落在竖直墙角的N点，不计空气阻力，下列选项中正确的是( )
A．v1>v2 B．v1C．t1>t2 D．t1＝t2
答案 A
解析 小球在竖直方向上为自由落体运动，则根据t＝eq \r(\f(2h,g))可知，t1x2，则v1>v2，故选A.
题型三：不同高不同速平抛
例3.(2020·江苏高考)(多选)如图所示，小球A、B分别从2l和l的高度水平抛出后落地，上述过程中A、B的水平位移分别为l和2l。忽略空气阻力，则( )
A．A和B的位移大小相等
B．A的运动时间是B的2倍
C．A的初速度是B的eq \f(1,2)
D．A的末速度比B的大
答案 AD
解析 位移为由初位置到末位置的有向线段，由图可得A、B的位移大小分别为sA＝ eq \r(l2＋2l2)＝eq \r(5)l，sB＝eq \r(2l2＋l2)＝eq \r(5)l，故A和B的位移大小相等，A正确；小球A、B在竖直方向上做自由落体运动，则A、B的运动时间分别为tA＝eq \r(\f(2×2l,g))＝2eq \r(\f(l,g))，tB＝eq \r(\f(2l,g))，故A的运动时间是B的eq \r(2)倍，B错误；小球A、B在水平方向上做匀速直线运动，则A、B的初速度分别为vxA＝eq \f(l,tA)＝eq \f(\r(gl),2)，vxB＝eq \f(2l,tB)＝eq \r(2gl)，故A的初速度是B的eq \f(1,2\r(2))，C错误；小球A、B在竖直方向上的末速度分别为vyA＝eq \r(2g·2l)＝2eq \r(gl)，vyB＝eq \r(2gl)，所以A、B的末速度分别为vA＝eq \r(v\\al(2,xA)＋v\\al(2,yA))＝eq \f(\r(17gl),2)，vB＝eq \r(v\\al(2,xB)＋v\\al(2,yB))＝2eq \r(gl)＝eq \f(\r(16gl),2)，故A的末速度比B的大，D正确。
题型四：以不同的速度从同一点平抛（临界 问题）
例4：如图所示，水平屋顶高H＝5 m，围墙高h＝3.2 m，围墙到房子的水平距离L＝3 m，围墙外空地宽x＝10 m，为使小球从屋顶①水平飞出②落在围墙外的空地上，g取10 m/s2。求：
(1)小球离开屋顶时的速度③v0的大小范围；
(2)小球落在空地上的④最小速度。
答案：5 m/s≤v0≤13 m/s；vmin＝5eq \r(5) m/s
解析：
(1)设小球恰好落到空地的右侧边缘时的水平初速度为v1，则小球的水平位移：
L＋x＝v1t1
小球的竖直位移：
H＝eq \f(1,2)gteq \\al(2,1)解以上两式得：
v1＝(L＋x) eq \r(\f(g,2H))＝13 m/s
设小球恰好越过围墙的边缘时的水平初速度为v2，则此过程中小球的水平位移：
L＝v2t2
小球的竖直位移：
H－h＝eq \f(1,2)gteq \\al(2,2)
解以上两式得：
v2＝L eq \r(\f(g,2H－h))＝5 m/s
小球抛出时的速度大小范围为5 m/s≤v0≤13 m/s
(2)小球落在空地上，下落高度一定，落地时的竖直分速度一定，当小球恰好越过围墙的边缘落在空地上时，落地速度最小。竖直方向：
veq \\al(2,y)＝2gH
又有：vmin＝eq \r(v\\al(2,2)＋v\\al(2,y))
解得：vmin＝5eq \r(5) m/s。
三.举一反三，巩固练习
1．人站在平台上平抛一小球，球离手时的速度为v1，落地时速度为v2，不计空气阻力，下列图中能表示出速度矢量的演变过程的是( )
2．(2018·江苏高考)某弹射管每次弹出的小球速度相等。在沿光滑竖直轨道自由下落过程中，该弹射管保持水平，先后弹出两只小球。忽略空气阻力，两只小球落到水平地面的( )
A．时刻相同，地点相同 B.时刻相同，地点不同
C．时刻不同，地点相同 D.时刻不同，地点不同
3．(2017·全国卷Ⅰ)发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。速度较大的球越过球网，速度较小的球没有越过球网。其原因是( )
A．速度较小的球下降相同距离所用的时间较多
B．速度较小的球在下降相同距离时在竖直方向上的速度较大
C．速度较大的球通过同一水平距离所用的时间较少
D．速度较大的球在相同时间间隔内下降的距离较大
4．如图所示，边长为a的正方体无盖盒子ABCD－A′B′C′D′放置在水平地面上，O为直线A′B′上的一点，且与A′的距离为a。将小球(可视为质点)从O点正上方距离2a处以某一速度水平抛出，不计空气阻力，重力加速度为g。为使小球能落在盒子内部，则小球抛出时的速度不超过( )
A. eq \r(\f(5,2)ga) B. eq \r(\f(5,4)ga)
C.eq \r(2ga) D.eq \r(ga)
5.有一半圆形轨道在竖直平面内，如图，O为圆心，AB为水平直径，有一小球(可视为质点)从A点以不同速度向右平抛，不计空气阻力，在小球从抛出到碰到轨道这个过程中，下列说法错误的是( )
A．初速度越大的小球运动时间不一定越长
B．初速度不同的小球运动时间可能相同
C．只需知道半圆形轨道半径R和重力加速度g，就可算出落在半圆形轨道最低点的小球的末速度
D．小球落到半圆形轨道的瞬间，速度方向可能沿半径方向
6．如图所示，水平地面的上空有一架飞机在进行投弹训练，飞机沿水平方向做匀加速直线运动。当飞机飞过观察点B正上方的A点时投放一颗炸弹，经时间T炸弹落在观察点B正前方L1处的C点，与此同时飞机投放出第二颗炸弹，第二颗炸弹最终落在观察点B正前方L2处的D点，且L2＝3L1。空气阻力不计，以下说法正确的是( )
A．飞机第一次投弹时的速度为eq \f(L1,2T)
B．飞机第二次投弹时的速度为eq \f(2L1,T)
C．飞机水平飞行的加速度为eq \f(L1,2T2)
D．两次投弹时间间隔T内飞机飞行的距离为eq \f(4L1,3)
7． 2019年9月的女排世界杯在东京举行，最终中国女排以11战全胜且只丢3局的成绩成功卫冕世界杯冠军，这也是中国女排第五次夺冠。如图所示，在一次比赛中，中国女排运动员朱婷将球在边界处正上方正对球网水平向前击出，球刚好过网落在图中位置(不计空气阻力)，相关数据如图所示，下列说法中正确的是( )
A．击球点高度h1与球网高度h2之间的关系为h1＝1.8h2
B．若保持击球高度不变，球的初速度满足eq \f(s,h1) eq \r(\f(gh1,2))C．任意降低击球高度(仍大于h2)，只要击球初速度合适，球一定能落在对方界内
D．任意增加击球高度，只要击球初速度合适，球一定能落在对方界内
8.(多选)从竖直墙的前方A处，沿AO方向水平发射三颗弹丸a、b、c，在墙上留下的弹痕如图所示，已知Oa＝ab＝bc，则a、b、c三颗弹丸(不计空气阻力)( )
A．初速度大小之比是eq \r(6)∶eq \r(3)∶eq \r(2)
B．初速度大小之比是1∶eq \r(2)∶eq \r(3)
C．从射出至打到墙上过程速度增量之比是1∶eq \r(2)∶eq \r(3)
D．从射出至打到墙上过程速度增量之比是eq \r(6)∶eq \r(3)∶eq \r(2)
9.如图所示，一竖直圆弧形槽固定于水平地面上，O为圆心，AB为沿水平方向的直径．若在A点以初速度v1沿AB方向平抛一小球，小球将击中槽壁上的最低点D点；若A点小球抛出的同时，在C点以初速度v2沿BA方向平抛另一相同质量的小球并也能击中D点，已知∠COD＝60°，且不计空气阻力，则( )
A．两小球同时落到D点
B．两小球初速度大小之比为eq \r(6)∶3
C．两小球落到D点时的速度方向与OD线夹角相等
D．两小球落到D点时的瞬时速率之比为eq \r(2)∶1
10.(多选)如图，在同一竖直面内，小球a、b从高度不同的两点，分别以初速度va和vb沿水平方向先后抛出，恰好同时落到地面上与两抛出点水平距离相等的P点，并且落到P点时两球的速度互相垂直．若不计空气阻力，则( )
A．小球a比小球b先抛出
B．初速度va小于vb
C．小球a、b抛出点距地面高度之比为vb∶va
D．初速度va大于vb
11．在水平路面上做匀速直线运动的小车上有一固定的竖直杆，竖直杆上的三个水平支架上有三个完全相同的小球A、B、C，它们离地面的高度分别为3h、2h和h，当小车遇到障碍物P时，立即停下来，三个小球同时从支架上水平抛出，先后落到水平路面上，如图所示，不计空气阻力，则下列说法正确的是( )
A．三个小球落地时间差与车速有关 B．三个小球落地点的间隔距离L1＝L2
C．三个小球落地点的间隔距离L1L2
12.斜面上有a、b、c、d四个点，如图所示，ab＝bc＝cd，从a点正上方的O点以速度v水平抛出一个小球，它落在斜面上b点，若小球从O点以速度2v水平抛出，不计空气阻力，则它落在斜面上的( )
A．b与c之间某一点 B．c点
C．c与d之间某一点 D．d点
四.举一反三，巩固练习参考答案
1．人站在平台上平抛一小球，球离手时的速度为v1，落地时速度为v2，不计空气阻力，下列图中能表示出速度矢量的演变过程的是( )
答案 C
解析 小球做平抛运动，只受重力作用，加速度方向竖直向下，所以速度变化的方向竖直向下，C正确．
2．(2018·江苏高考)某弹射管每次弹出的小球速度相等。在沿光滑竖直轨道自由下落过程中，该弹射管保持水平，先后弹出两只小球。忽略空气阻力，两只小球落到水平地面的( )
A．时刻相同，地点相同 B.时刻相同，地点不同
C．时刻不同，地点相同 D.时刻不同，地点不同
答案 B
解析 弹射管在竖直方向做自由落体运动，所以弹出小球在竖直方向运动的时间相等，因此两球应同时落地；由于两小球先后弹出，所以小球在水平方向运动的时间不等，因小球在水平方向做匀速运动，且弹出小球的水平初速度相同，所以水平位移不相等，因此落点不相同，故B正确。
3．(2017·全国卷Ⅰ)发球机从同一高度向正前方依次水平射出两个速度不同的乒乓球(忽略空气的影响)。速度较大的球越过球网，速度较小的球没有越过球网。其原因是( )
A．速度较小的球下降相同距离所用的时间较多
B．速度较小的球在下降相同距离时在竖直方向上的速度较大
C．速度较大的球通过同一水平距离所用的时间较少
D．速度较大的球在相同时间间隔内下降的距离较大
答案 C
解析 在竖直方向，球做自由落体运动，由h＝eq \f(1,2)gt2知，选项A、D错误。由v2＝2gh知，选项B错误。在水平方向，球做匀速直线运动，通过相同水平距离，速度大的球用时少，选项C正确。
4．如图所示，边长为a的正方体无盖盒子ABCD－A′B′C′D′放置在水平地面上，O为直线A′B′上的一点，且与A′的距离为a。将小球(可视为质点)从O点正上方距离2a处以某一速度水平抛出，不计空气阻力，重力加速度为g。为使小球能落在盒子内部，则小球抛出时的速度不超过( )
A. eq \r(\f(5,2)ga) B. eq \r(\f(5,4)ga)
C.eq \r(2ga) D.eq \r(ga)
答案 A
解析 依题意，可知小球以最大速度水平抛出能落到盒子内时，恰好落到C点，有a＝eq \f(1,2)gt2，xOC′＝vmaxt，根据几何知识，有xOC′＝eq \r(2a2＋a2)＝eq \r(5)a，联立解得vmax＝eq \r(\f(5,2)ga)，故A正确。

5.有一半圆形轨道在竖直平面内，如图，O为圆心，AB为水平直径，有一小球(可视为质点)从A点以不同速度向右平抛，不计空气阻力，在小球从抛出到碰到轨道这个过程中，下列说法错误的是( )
A．初速度越大的小球运动时间不一定越长
B．初速度不同的小球运动时间可能相同
C．只需知道半圆形轨道半径R和重力加速度g，就可算出落在半圆形轨道最低点的小球的末速度
D．小球落到半圆形轨道的瞬间，速度方向可能沿半径方向
答案 D
解析 平抛运动的时间由下落高度决定，与水平初速度无关，初速度大时与半圆轨道接触时下落的距离不一定比初速度小时下落的距离大，即初速度越大的小球运动时间不一定越长，故A正确；初速度不同的小球下落的高度可能相等，运动时间可能相等，如碰撞点关于半圆过O点的竖直轴对称时，故B正确；小球落到半圆形轨道最低点时，根据平抛运动规律，有R＝v0t，R＝eq \f(1,2)gt2，解得v0＝ eq \r(\f(gR,2))，则落到半圆形轨道最低点时的速度v＝eq \r(v\\al(2,0)＋2gR)＝eq \r(\f(5,2)gR)，即只需知道半圆形轨道半径R和重力加速度g，就可算出落在半圆形轨道最低点的小球的末速度，C正确；若小球落到半圆形轨道的瞬间，速度方向沿半径方向，则速度的反向延长线过O点，而此时水平位移的中点在O点左侧，则与平抛运动的推论(平抛运动速度的反向延长线过水平位移的中点)矛盾，即小球落到半圆形轨道的瞬间速度方向不会沿半径方向，故D错误。本题选说法错误的，故选D。
6．如图所示，水平地面的上空有一架飞机在进行投弹训练，飞机沿水平方向做匀加速直线运动。当飞机飞过观察点B正上方的A点时投放一颗炸弹，经时间T炸弹落在观察点B正前方L1处的C点，与此同时飞机投放出第二颗炸弹，第二颗炸弹最终落在观察点B正前方L2处的D点，且L2＝3L1。空气阻力不计，以下说法正确的是( )
A．飞机第一次投弹时的速度为eq \f(L1,2T)
B．飞机第二次投弹时的速度为eq \f(2L1,T)
C．飞机水平飞行的加速度为eq \f(L1,2T2)
D．两次投弹时间间隔T内飞机飞行的距离为eq \f(4L1,3)
答案 D
解析 由平抛运动规律可知飞机第一次投弹时的速度v1＝eq \f(L1,T)，故A错误；设飞机加速度为a，第二次投弹时的速度为v2，由匀变速直线运动规律可知v1T＋eq \f(1,2)aT2＝L2－(v1＋aT)T，而L2＝3L1，得a＝eq \f(2L1,3T2)，v2＝v1＋aT＝eq \f(5L1,3T)，故B、C错误；两次投弹时间间隔T内飞机飞行的距离s＝v1T＋eq \f(1,2)aT2＝eq \f(4L1,3)，故D正确。
7． 2019年9月的女排世界杯在东京举行，最终中国女排以11战全胜且只丢3局的成绩成功卫冕世界杯冠军，这也是中国女排第五次夺冠。如图所示，在一次比赛中，中国女排运动员朱婷将球在边界处正上方正对球网水平向前击出，球刚好过网落在图中位置(不计空气阻力)，相关数据如图所示，下列说法中正确的是( )
A．击球点高度h1与球网高度h2之间的关系为h1＝1.8h2
B．若保持击球高度不变，球的初速度满足eq \f(s,h1) eq \r(\f(gh1,2))C．任意降低击球高度(仍大于h2)，只要击球初速度合适，球一定能落在对方界内
D．任意增加击球高度，只要击球初速度合适，球一定能落在对方界内
答案 AD
解析 做平抛运动的球在水平方向上做匀速直线运动，水平位移为s和eq \f(3s,2)所用的时间比为2∶3，则竖直方向上，根据h＝eq \f(1,2)gt2，有eq \f(h1－h2,h1)＝eq \f(4,9)，解得h1＝1.8h2，故A正确；若保持击球高度不变，要想球落在对方界内，且既不能出界，又不能触网，根据h1＝eq \f(1,2)gteq \\al(2,1)，得t1＝ eq \r(\f(2h1,g))，则平抛运动的最大初速度v01＝eq \f(2s,t1)＝eq \f(s,h1) eq \r(2gh1)，根据h1－h2＝eq \f(1,2)gteq \\al(2,2)，得t2＝ eq \r(\f(2h1－h2,g))，则平抛运动的最小初速度v02＝eq \f(s,t2)＝seq \r(\f(g,2h1－h2))，故B错误；任意降低击球高度(仍大于h2)，会有一临界情况，此时球刚好触网又刚好压界，若小于该临界高度，速度大会出界，速度小会触网，所以击球高度比网高，不一定能将球发到对方界内，故C错误；任意增加击球高度，只要击球初速度合适，球一定能落到对方界内，故D正确。
8.(多选)从竖直墙的前方A处，沿AO方向水平发射三颗弹丸a、b、c，在墙上留下的弹痕如图所示，已知Oa＝ab＝bc，则a、b、c三颗弹丸(不计空气阻力)( )
A．初速度大小之比是eq \r(6)∶eq \r(3)∶eq \r(2)
B．初速度大小之比是1∶eq \r(2)∶eq \r(3)
C．从射出至打到墙上过程速度增量之比是1∶eq \r(2)∶eq \r(3)
D．从射出至打到墙上过程速度增量之比是eq \r(6)∶eq \r(3)∶eq \r(2)
答案 AC
解析 水平发射的弹丸做平抛运动，竖直方向上是自由落体运动，水平方向上是匀速直线运动，又因为竖直方向上Oa＝ab＝bc，即Oa∶Ob∶Oc＝1∶2∶3，由h＝eq \f(1,2)gt2可知ta∶tb∶tc＝1∶eq \r(2)∶eq \r(3)，由水平方向x＝v0t可得va∶vb∶vc＝1∶eq \f(1,\r(2))∶eq \f(1,\r(3))＝eq \r(6)∶eq \r(3)∶eq \r(2)，故选项A正确，B错误；由Δv＝gt，可知从射出至打到墙上过程速度增量之比是1∶eq \r(2)∶eq \r(3)，故选项C正确，D错误．
9.如图所示，一竖直圆弧形槽固定于水平地面上，O为圆心，AB为沿水平方向的直径．若在A点以初速度v1沿AB方向平抛一小球，小球将击中槽壁上的最低点D点；若A点小球抛出的同时，在C点以初速度v2沿BA方向平抛另一相同质量的小球并也能击中D点，已知∠COD＝60°，且不计空气阻力，则( )
A．两小球同时落到D点
B．两小球初速度大小之比为eq \r(6)∶3
C．两小球落到D点时的速度方向与OD线夹角相等
D．两小球落到D点时的瞬时速率之比为eq \r(2)∶1
答案 B
解析 由于A、C两点到D点的竖直高度不同，两球在空中运动时间不同，A选项错误；设圆弧形槽半径为R，对A点抛出的小球，R＝v1tA，tA＝ eq \r(\f(2R,g))，则v1＝Req \r(\f(g,2R))＝ eq \r(\f(1,2)gR)，
对C点抛出的小球，Rsin 60°＝v2tC，tC＝eq \r(\f(R－Rcs 60°×2,g))＝eq \r(\f(R,g))，则v2＝eq \f(\r(3)R,2)eq \r(\f(g,R))＝ eq \r(\f(3,4)gR)，v1∶v2＝eq \r(6)∶3，B选项正确；
设在D点速度方向与OD线夹角为θ，竖直分速度为vy，水平分速度为v0，则tan θ＝eq \f(v0,vy)
由v1∶v2＝eq \r(6)∶3
vy1∶vy2＝tA∶tC＝eq \r(2)∶1
tan θ1≠tan θ2，C选项错误；
设A、C两点抛出球落到D点时的瞬时速率分别为vA、vC，vA＝eq \r(v\\al(12,)＋v\\al(y12,))＝eq \r(\f(5,2)gR)，vC＝eq \r(v\\al(22,)＋v\\al(y22,))＝eq \r(\f(7,4)gR)，则vA∶vC＝eq \r(10)∶eq \r(7)，D选项错误．
10.(多选)如图，在同一竖直面内，小球a、b从高度不同的两点，分别以初速度va和vb沿水平方向先后抛出，恰好同时落到地面上与两抛出点水平距离相等的P点，并且落到P点时两球的速度互相垂直．若不计空气阻力，则( )
A．小球a比小球b先抛出
B．初速度va小于vb
C．小球a、b抛出点距地面高度之比为vb∶va
D．初速度va大于vb
答案 AB
解析 h＝eq \f(1,2)gt2，所以t＝eq \r(\f(2h,g))，平抛运动的运动时间是由竖直的高度决定的，由于小球a的高度比小球b的大，所以 ta＞tb，由于小球a、b的水平位移相等，由x＝v0t得
va＜vb，故A、B正确，D错误．h＝eq \f(1,2)gt2＝eq \f(1,2)geq \f(x2,v\\al(02,))，故小球a、b抛出点距地面高度之比为eq \f(ha,hb)＝eq \f(v\\al(b2,),v\\al(a2,))，C错误．
11．在水平路面上做匀速直线运动的小车上有一固定的竖直杆，竖直杆上的三个水平支架上有三个完全相同的小球A、B、C，它们离地面的高度分别为3h、2h和h，当小车遇到障碍物P时，立即停下来，三个小球同时从支架上水平抛出，先后落到水平路面上，如图所示，不计空气阻力，则下列说法正确的是( )
A．三个小球落地时间差与车速有关
B．三个小球落地点的间隔距离L1＝L2
C．三个小球落地点的间隔距离L1D．三个小球落地点的间隔距离L1>L2
答案 C
解析 平抛运动中，落地时间只与下落的高度有关，故A项错误；三个小球在竖直方向上做自由落体运动，由公式t＝eq \r(\f(2h,g))可得下落时间之比为tA∶tB∶tC＝eq \r(3)∶eq \r(2)∶1，由于三个小球初速度相同，故水平位移之比xA∶xB∶xC＝eq \r(3)∶eq \r(2)∶1，则L1∶L2＝(eq \r(3)－eq \r(2))∶(eq \r(2)－1)，故L112.斜面上有a、b、c、d四个点，如图所示，ab＝bc＝cd，从a点正上方的O点以速度v水平抛出一个小球，它落在斜面上b点，若小球从O点以速度2v水平抛出，不计空气阻力，则它落在斜面上的( )
A．b与c之间某一点 B．c点
C．c与d之间某一点 D．d点
答案：A
[解析] 假设斜面是一层很薄的纸，小球落上就可穿透且不损失能量，过b点作水平线交Oa于a′，由于小球从O点以速度v水平抛出时，落在斜面上b点，则小球从O点以速度2v水平抛出，穿透斜面后应落在水平线a′b延长线上的c′点，如图所示，因ab＝bc，则a′b＝bc′，即c′点在c点的正下方，显然，小球轨迹交于斜面上b与c之间。所以，本题答案应选A。