初中数学人教版八年级上册12.2 三角形全等的判定教学设计

这是一份初中数学人教版八年级上册12.2 三角形全等的判定教学设计，共3页。
初中数学
年级/册
八年级上册
教材版本
人教版
课题名称
第十二章12.2：三角形全等的判定
教学目标
为什么没有边边角公理？
重难点分析
重点分析
“两边一角问题”是在学生学习了边边边公理后学习探究的内容，“两边夹一角”好理解，但是，为什么没有边边角公理？课本上虽然给出了说明，但是条件有些相似，容易混淆关系。
难点分析
学生很容易理解两边夹一角公理，因为他们通过画图，剪纸的方法进行了验证，但是他们忽视了“边边角条件”能否识别两三角形全等，所以往往凭感觉用边边角方法来证明两个三角形全等。
教学方法
通过观察，画图，比较，用几何画板演示动画，启发学生思考再推理论证。
教学环节
教学过程
导入
A
B
C
D
E
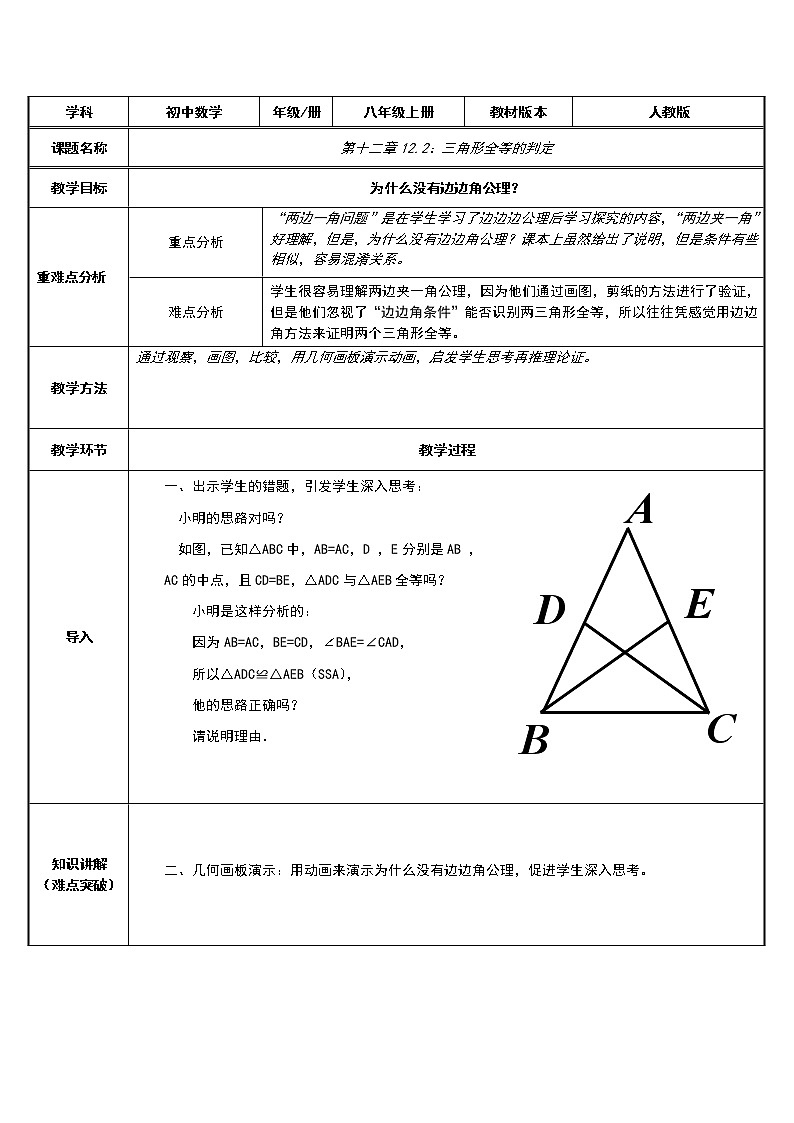
出示学生的错题，引发学生深入思考：
小明的思路对吗？
如图，已知△ABC中，AB=AC，D ，E分别是AB ，
AC的中点，且CD=BE，△ADC与△AEB全等吗？
小明是这样分析的：
因为AB=AC，BE=CD，∠BAE=∠CAD，
所以△ADC≌△AEB（SSA），
他的思路正确吗？
请说明理由．
知识讲解
（难点突破）
几何画板演示：用动画来演示为什么没有边边角公理，促进学生深入思考。
课堂练习
（难点巩固）

探索“SSA”能否识别两三角形全等：
提出问题：两边一角分别相等包括“两边夹角”和
“两边及其中一边的对角”分别相等两种情况，前面已
探索出“SAS”判定三角形全等的方法，那么由“SSA”
的条件能判定两个三角形全等吗？
2.得出结论：如图，在△ABC 和△ABD 中， AB =AB，AC = AD，∠B =∠B，
但△ABC 和△ABD 不全等．
C
B
A
三．学生错误分析：
思路错误．小明错把“SSA”作为三角形全等的判别方法，两边及一边对角相等的两个三角形不一定全等．
A
B
C
D
E
四：正确的两种解法：
正确的解法1：△ADC≌△AEB．
∵AB=AC，D，E为AB，AC的中点，
∴AD=AE．
在△ADC和△AEB中，
∵AC=AB，AD=AE，CD=BE，
∴△ADC≌△AEB（SSS）．
另一种解法：
∵AB=AC，D，E为AB，AC的中点，
∴AD=AE．
在△ADC和△AEB中，
∵AC=AB，∠CAD=∠BAE，AD=AE，
∴△ADC≌△AEB（SAS）．
小结
课堂小结：1．根据“边角边”判定两个三角形全等，要找出
两边及夹角分别相等的三个条件．
2．找使结论成立所需条件，要充分利用已知条件
（包括给出图形中的隐含条件，如公共边、公共
角等），并要善于运用学过的定义、公理、定理．