2020-2021学年安徽省淮南市田家庵区八年级（下）期末数学试卷

这是一份2020-2021学年安徽省淮南市田家庵区八年级（下）期末数学试卷，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2020-2021学年安徽省淮南市田家庵区八年级（下）期末数学试卷
一、选择题（共10小题，每小题3分，共30分）
1．（3分）下列各式中，，﹣，，一定是二次根式的有（　　）个．
A．2 B．3 C．4 D．5
2．（3分）若平行四边形中两个相邻内角的度数之比为1：3，则其中较小的内角是（　　）
A．45° B．30° C．60° D．36°
3．（3分）为调查某班学生每天使用零花钱的情况，张华随机调查了30名同学，结果如下：
每天使用零花钱（单位：元）
1
2
3
4
5
人数
2
5
8
9
6
则这30名同学每天使用零花钱的众数和中位数分别是（　　）
A．4，3 B．4，3.5 C．9，3.5 D．9，8.5
4．（3分）下列计算正确的是（　　）
A．＝ B．＝
C．＝1 D．（）（）＝1
5．（3分）如图，在4×4的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，AD⊥BC于D，则AD的长为（　　）

A．1 B．2 C． D．
6．（3分）一组数据3，4，4，5，若添加一个数4，则发生变化的统计量是（　　）
A．平均数 B．众数 C．中位数 D．方差
7．（3分）如图所示，在▱ABCD中，AC与BD相交于点O，过点O作直线m交线段AB于点E，交线段CD于点F，则图中共有几对全等三角形（　　）

A．4 B．5 C．6 D．7
8．（3分）在△ABC中，若AB＝3，BC＝5，AC＝，则下列说法正确的是（　　）
A．△ABC是锐角三角形
B．△ABC是直角三角形且∠C＝90°
C．△ABC是钝角三角形
D．△ABC是直角三角形且∠B＝90°
9．（3分）如图，在矩形ABCD中，AB＝3，AD＝4，AE平分∠BAD交BC于点E．点F，G分别是AD，AE的中点，则FG的长为（　　）

A． B． C．2 D．
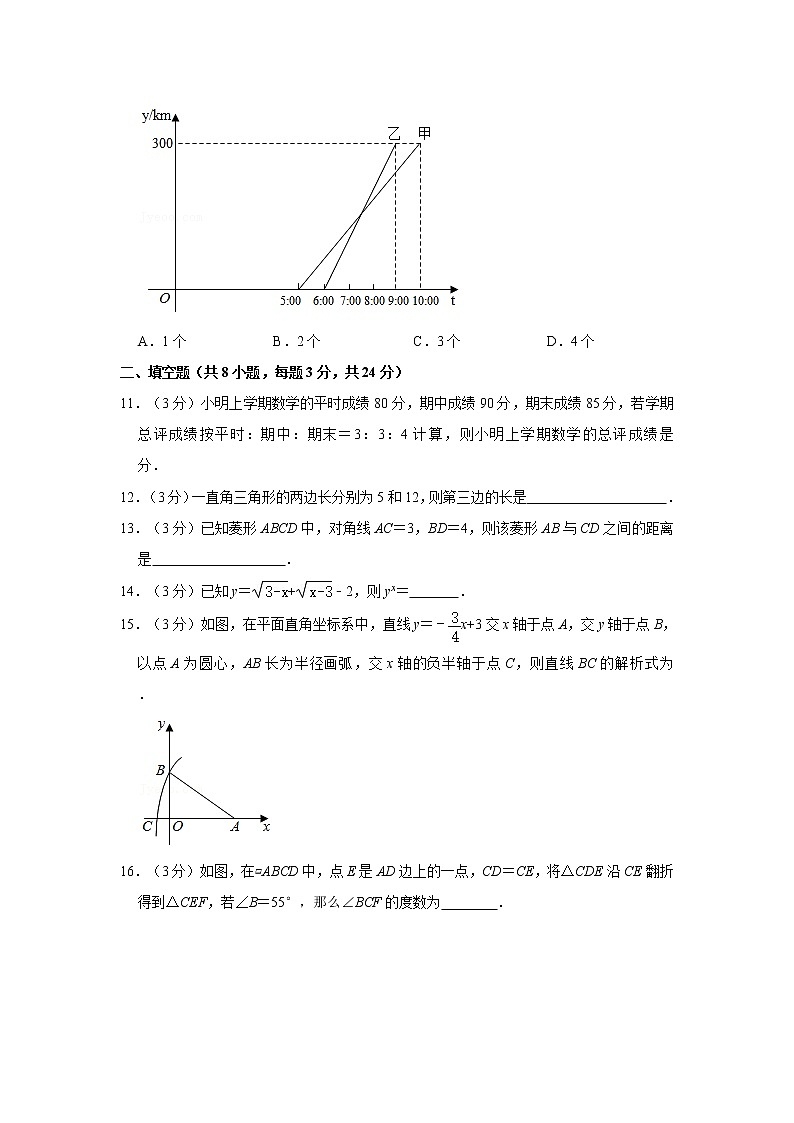
10．（3分）如图，甲、乙两汽车从A城出发前往B城，在整个行程中，汽车离开A城的距离y（km）与时间t的对应关系如图所示．下列结论：①A，B两城相距300km；②行程中甲、乙两车的速度比为2：3；③乙车于7：20追上甲车；④9：00时，甲、乙两车相距60km．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
二、填空题（共8小题，每题3分，共24分）
11．（3分）小明上学期数学的平时成绩80分，期中成绩90分，期末成绩85分，若学期总评成绩按平时：期中：期末＝3：3：4计算，则小明上学期数学的总评成绩是　 　分．
12．（3分）一直角三角形的两边长分别为5和12，则第三边的长是　 　．
13．（3分）已知菱形ABCD中，对角线AC＝3，BD＝4，则该菱形AB与CD之间的距离是　 　．
14．（3分）已知y＝+﹣2，则yx＝　 　．
15．（3分）如图，在平面直角坐标系中，直线y＝﹣x+3交x轴于点A，交y轴于点B，以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则直线BC的解析式为　 　．

16．（3分）如图，在▱ABCD中，点E是AD边上的一点，CD＝CE，将△CDE沿CE翻折得到△CEF，若∠B＝55°，那么∠BCF的度数为　 　．

17．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，直线l1：y＝k1x+b交x轴于点（﹣3，0），则关于x的不等式k2x＜k1x+b＜0的解集为　 　．

18．（3分）如图，点P是Rt△ABC中斜边AC（不与A，C重合）上一动点，分别作PM⊥AB点M，作PN⊥BC于点N，点O是MN的中点，若AB＝6，BC＝8，当点P在AC上运动时，则BO的最小值是 　 　．

三、解答题（共5题，共46分）
19．（8分）计算：
（1）；
（2）．
20．（8分）某校检测学生跳绳水平，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图

（1）D组的人数是 　 　人，补全频数分布直方图，扇形图中m＝　 　；
（2）本次调查数据中的中位数落在 　 　组；
（3）如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人？
21．（8分）如图，在平面直角坐标系中，直线y1＝2x和直线y2＝﹣x+m相交于点A，且点A的纵坐标为2，点B在线段OA上（不与O、A重合），过点B作BC∥x轴（自己完成）交直线y2＝﹣x+m于点C．
（1）求m的值；
（2）若线段BC＝2，请直接写出点B的坐标　 　．

22．（10分）某花农要将规格相同的800棵平安树运往A，B，C三地销售，要求运往C地的棵数是运往A地棵数的3倍，各地的运费如表所示：

A地
B地
C地
运费（元/棵）
10
20
15
（1）设运往A地的平安树x（棵），总运费为y（元）试写出y与x的函数关系式；
（2）若要求运往A地的平安树不超过运往B地的平安树，且总运费不超过14000元，问当运往A地的平安树多少棵时，总运费才最省？
23．（12分）已知，在▱ABCD中，AE⊥BC于点E，AF⊥CD于点F，且AE＝AF．
（1）如图1，当EC＝4，AE＝8时，求▱ABCD的对角线BD的长；
（2）如图2，若点M为CD的中点，连接EM，AM．求证：AM＝EM．


2020-2021学年安徽省淮南市田家庵区八年级（下）期末数学试卷
参考答案与试题解析
一、选择题（共10小题，每小题3分，共30分）
1．（3分）下列各式中，，﹣，，一定是二次根式的有（　　）个．
A．2 B．3 C．4 D．5
【分析】根据二次根式定义：一般地，我们把形如（a≥0）的式子叫做二次根式进行分析即可．
【解答】解：，﹣，一定是二次根式，共3个，
故选：B．
2．（3分）若平行四边形中两个相邻内角的度数之比为1：3，则其中较小的内角是（　　）
A．45° B．30° C．60° D．36°
【分析】首先设平行四边形中两个内角分别为x°，3x°，由平行四边形的邻角互补，即可得x+3x＝180，继而求得答案．
【解答】解：设平行四边形中两个相邻内角分别为x°，3x°，
则x+3x＝180，
解得：x＝45，
∴其中较小的内角是45°，
故选：A．
3．（3分）为调查某班学生每天使用零花钱的情况，张华随机调查了30名同学，结果如下：
每天使用零花钱（单位：元）
1
2
3
4
5
人数
2
5
8
9
6
则这30名同学每天使用零花钱的众数和中位数分别是（　　）
A．4，3 B．4，3.5 C．9，3.5 D．9，8.5
【分析】利用众数的定义可以确定众数在第三组，由于随机调查了30名同学，根据表格数据可以知道中位数是按从小到大排序，第15个与第16个数的平均数．
【解答】解：∵4出现了9次，它的次数最多，
∴众数为4．
∵随机调查了30名同学，
∴根据表格数据可以知道中位数＝（3+4）÷2＝3.5，即中位数为3.5．
故选：B．
4．（3分）下列计算正确的是（　　）
A．＝ B．＝
C．＝1 D．（）（）＝1
【分析】根据二次根式的加减法对A进行判断；根据二次根式的乘法法则对B进行判断；利用分母有理化对C进行判断；根据平方差公式对D进行判断．
【解答】解：A、与不能合并，所以A选项错误；
B、原式＝＝，所以B选项错误；
C、原式＝，所以C选项错误；
D、原式＝3﹣2＝1，所以D选项正确．
故选：D．
5．（3分）如图，在4×4的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，AD⊥BC于D，则AD的长为（　　）

A．1 B．2 C． D．
【分析】根据勾股定理计算BC的长，利用面积差可得三角形ABC的面积，由三角形的面积公式即可得到结论．
【解答】解：由勾股定理得：BC＝＝5，
∵S△ABC＝4×4﹣×1×2﹣×2×4﹣×4×3＝5，
∴BC•AD＝5，
∴AD＝5，
∴AD＝2．
故选：B．
6．（3分）一组数据3，4，4，5，若添加一个数4，则发生变化的统计量是（　　）
A．平均数 B．众数 C．中位数 D．方差
【分析】依据的定义和公式分别计算新旧两组数据的平均数、中位数、众数、方差求解即可．
【解答】解：原数据的3，4，5，4的平均数为＝4，中位数为4，众数为4，方差为×[（3﹣4）2+（4﹣4）2×2+（5﹣4）2]＝0.5；
新数据3，4，4，4，5的平均数为＝4，中位数为4，众数为4，方差为×[（3﹣4）2+（4﹣4）2×3+（5﹣4）2]＝0.4；
所以发生变化的是方差，
故选：D．
7．（3分）如图所示，在▱ABCD中，AC与BD相交于点O，过点O作直线m交线段AB于点E，交线段CD于点F，则图中共有几对全等三角形（　　）

A．4 B．5 C．6 D．7
【分析】利用平行四边形的性质和全等三角形的判定可求解．
【解答】解：∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝BC，AD∥BC，AB∥CD，AO＝CO，BO＝DO，
∴∠CAB＝∠ACD，
在△ABC和△CAD中，
，
∴△ABC≌△CAD（SSS），
同理可得△ABD≌△CDB，
在△AOE和△COF中，
，
∴△AOE≌△COF（ASA），
同理可得△BOE≌△COF，△AOB≌△COD，△AOD≌△COB，
∴共有6对全等三角形，
故选：C．
8．（3分）在△ABC中，若AB＝3，BC＝5，AC＝，则下列说法正确的是（　　）
A．△ABC是锐角三角形
B．△ABC是直角三角形且∠C＝90°
C．△ABC是钝角三角形
D．△ABC是直角三角形且∠B＝90°
【分析】先分别求出两小边的平方和和最长的边的平方，再看看是否相等即可．
【解答】解：在△ABC中，AB＝3，BC＝5，AC＝，
∴AC2＝34，AB2+BC2＝9+25＝34，
∴AC2＝AB2+BC2，
∴△ABC是直角三角形，∠B＝90°，
故选：D．
9．（3分）如图，在矩形ABCD中，AB＝3，AD＝4，AE平分∠BAD交BC于点E．点F，G分别是AD，AE的中点，则FG的长为（　　）

A． B． C．2 D．
【分析】连接DE，由矩形的性质和角平分线的性质可得AB＝BE＝3，可得EC＝1，由勾股定理可求DE的长，由三角形中位线定理可求FG的长．
【解答】解：连接DE，如图所示：
∵四边形ABCD是矩形，
∴∠BAD＝∠B＝∠C＝90°，AB＝CD＝3，AD＝BC＝4，AD∥BC，
∴∠DAE＝∠AEB，
∵AE平分∠BAD，
∴∠DAE＝∠BAE＝45°，
∴∠BAE＝∠AEB，
∴AB＝BE＝3，
∴EC＝BC﹣BE＝1，
∴DE＝＝＝，
∵点F、G分别为AD、AE的中点，
∴FG是△ADE的中位线，
∴FG＝DE＝；
故选：A．

10．（3分）如图，甲、乙两汽车从A城出发前往B城，在整个行程中，汽车离开A城的距离y（km）与时间t的对应关系如图所示．下列结论：①A，B两城相距300km；②行程中甲、乙两车的速度比为2：3；③乙车于7：20追上甲车；④9：00时，甲、乙两车相距60km．其中正确的有（　　）

A．1个 B．2个 C．3个 D．4个
【分析】根据整个行程中，汽车离开A城的距离y与时刻t的对应关系，即可得到正确结论．
【解答】解：①由题可得，A，B两城相距300千米，故①结论正确；
②甲车的平均速度为：300÷（10﹣5）＝60（千米/时），乙车的平均速度为：300÷（9﹣6）＝100（千米/时），所以行程中甲、乙两车的速度比为3：5，故②结论错误；
③设乙出发x小时后追上了甲，则100x＝60（x+1），解得x＝1.5，即乙车于7：30追上甲车，故③结论错误；
④9：00时甲车所走路程为：60×（9﹣5）＝240（km），300﹣240＝60（km），即9：00时，甲、乙两车相距60km，故④结论正确；
所以正确的有①④共2个．
故选：B．
二、填空题（共8小题，每题3分，共24分）
11．（3分）小明上学期数学的平时成绩80分，期中成绩90分，期末成绩85分，若学期总评成绩按平时：期中：期末＝3：3：4计算，则小明上学期数学的总评成绩是　85　分．
【分析】根据加权平均数的计算公式计算可得．
【解答】解：根据题意，小明上学期数学的总评成绩是＝85（分），
故答案为：85．
12．（3分）一直角三角形的两边长分别为5和12，则第三边的长是　13或　．
【分析】本题已知直角三角形的两边长，但未明确这两条边是直角边还是斜边，因此两条边中的较长边4既可以是直角边，也可以是斜边，所以求第三边的长必须分类讨论，即12是斜边或直角边的两种情况，然后利用勾股定理求解．
【解答】解：设第三边为x，
（1）若12是直角边，则第三边x是斜边，由勾股定理得：
52+122＝x2，
∴x＝13；
（2）若12是斜边，则第三边x为直角边，由勾股定理得：
52+x2＝122，
∴x＝；
∴第三边的长为13或．
故答案为：13或．
13．（3分）已知菱形ABCD中，对角线AC＝3，BD＝4，则该菱形AB与CD之间的距离是　　．
【分析】由菱形的面积公式可求菱形的面积，即可求解．
【解答】解：∵AC＝3，BD＝4，
∴菱形ABCD的面积＝＝6，菱形的边长＝＝，
∴AB与CD之间的距离＝＝，
故答案为．
14．（3分）已知y＝+﹣2，则yx＝　﹣8　．
【分析】根据二次根式有意义的条件可得，解不等式组可得x＝3，然后可得y的值，再代入所求式子计算即可．
【解答】解：由题意得：，
解得：x＝3，
则y＝﹣2，
∴yx＝（﹣2）3＝﹣8．
故答案为：﹣8．
15．（3分）如图，在平面直角坐标系中，直线y＝﹣x+3交x轴于点A，交y轴于点B，以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，则直线BC的解析式为　y＝3x+3　．

【分析】先求得A、B的坐标，然后利用勾股定理得出AB的长，再利用圆的性质得出CO的长，即可得出C的坐标，然后根据待定系数法即可求得直线BC的解析式．
【解答】解：在直线y＝﹣x+3中，令y＝0，求得x＝4；令x＝0，求得y＝3，
∴点A的坐标为（4，0），点B的坐标为（0，3），
∴BO＝3，AO＝4，
∴AB＝＝5，
∵以点A为圆心，AB长为半径画弧，交x轴的负半轴于点C，
∴CO＝5﹣4＝1，
则点C的坐标为：（﹣1，0），
设直线BC的解析式为y＝kx+b，
把B（0，3），C（﹣1，0）代入得，解得，
∴直线BC的解析式为y＝3x+3．
故答案为y＝3x+3．
16．（3分）如图，在▱ABCD中，点E是AD边上的一点，CD＝CE，将△CDE沿CE翻折得到△CEF，若∠B＝55°，那么∠BCF的度数为　15°　．

【分析】由平行四边形的性质和等腰三角形的性质可得∠D＝∠CED＝55°，∠ECD＝70°，由折叠的性质可得∠ECD＝∠ECF＝70°，即可求解．
【解答】解：∵四边形ABCD是平行四边形，
∴∠B＝∠D＝55°，
∵CD＝CE，
∴∠D＝∠CED＝55°，
∴∠ECD＝70°，
∵AD∥BC，
∴∠DEC＝∠BCE＝55°，
∵将△CDE沿CE翻折得到△CEF，
∴∠ECD＝∠ECF＝70°，
∴∠BCF＝∠ECF﹣∠BCE＝15°，
故答案为：15°．
17．（3分）直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，直线l1：y＝k1x+b交x轴于点（﹣3，0），则关于x的不等式k2x＜k1x+b＜0的解集为　﹣3＜x＜﹣1　．

【分析】根据题意和函数图象，可以写出关于x的不等式k2x＜k1x+b＜0的解集，本题得以解决．
【解答】解：由图象可知，直线l1和直线l2的交点为（﹣1，﹣2），直线l1中y随x的增大而减小，
∵y＝k1x+b交x轴于点（﹣3，0），关于x的不等式k2x＜k1x+b的解集为x＜﹣1，
∴关于x的不等式k2x＜k1x+b＜0的解集是﹣3＜x＜﹣1，
故答案为：﹣3＜x＜﹣1．
18．（3分）如图，点P是Rt△ABC中斜边AC（不与A，C重合）上一动点，分别作PM⊥AB点M，作PN⊥BC于点N，点O是MN的中点，若AB＝6，BC＝8，当点P在AC上运动时，则BO的最小值是 　2.4　．

【分析】证四边形BMPN是矩形，得BP与MN互相平分，则BO＝BP，当BP⊥AC时，BP最小，再由面积法求出BP即可．
【解答】解：连接BP，如图所示：
∵PM⊥AB于点M，PN⊥BC于点N，
∴∠PMB＝∠PMB＝90°，
又∵∠ABC＝90°，
∴四边形BMPN是矩形，AC＝＝＝10，
∴BP与MN互相平分，
∵点O是MN的中点，
∴O是BP的中点，
∴BO＝BP，
当BP⊥AC时，BP最小，
此时，△ABC的面积＝AC×BP＝AB×BC，
∴BP最小值＝＝＝4.8，
∴BO的最小值＝BP＝2.4，
故答案为：2.4．

三、解答题（共5题，共46分）
19．（8分）计算：
（1）；
（2）．
【分析】（1）根据二次根式的加减法法则计算；
（2）根据平方差公式，二次根式的乘法法则计算．
【解答】解：（1）原式＝3﹣2++2
＝；
（2）原式＝（+2）（﹣2）
＝
＝15﹣12
＝3．
20．（8分）某校检测学生跳绳水平，抽样调查了部分学生的“1分钟跳绳”成绩，并制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图

（1）D组的人数是 　16　人，补全频数分布直方图，扇形图中m＝　84°　；
（2）本次调查数据中的中位数落在 　C　组；
（3）如果“1分钟跳绳”成绩大于或等于120次为优秀，那么该校4500名学生中“1分钟跳绳”成绩为优秀的大约有多少人？
【分析】（1）根据百分比＝，圆心角＝360°×百分比，计算即可；
（2）根据中位数的定义计算即可；
（3）用样本估计总体的思考问题即可；
【解答】解：（1）由题意总人数＝6÷10%＝60（人），
D组人数＝60﹣6﹣14﹣19﹣5＝16（人）．
B组的圆心角为360°×＝84°．
故答案为16、84°；
（2）本次调查数据中的中位数落在C组．
故答案为C；
（3）该校4500名学生中“1分钟跳绳”成绩为优秀的大约有4500×＝3000（人）．
21．（8分）如图，在平面直角坐标系中，直线y1＝2x和直线y2＝﹣x+m相交于点A，且点A的纵坐标为2，点B在线段OA上（不与O、A重合），过点B作BC∥x轴（自己完成）交直线y2＝﹣x+m于点C．
（1）求m的值；
（2）若线段BC＝2，请直接写出点B的坐标　（，）　．

【分析】（1）把y＝2代入y1＝2x，解得A的坐标，然后把A的坐标代入y2＝﹣x+m，即可求得m的值；
（2）设B点的纵坐标为n，则B（，n），C（3﹣n，n），根据题意得到3﹣n﹣＝2，解得n的值，即可求得B的坐标．
【解答】解：（1）∵直线y1＝2x和直线y2＝﹣x+m相交于点A，且点A的纵坐标为2，
∴把y＝2代入y1＝2x得，2＝2x，
∴x＝1，
∴A（1，2），
代入y2＝﹣x+m得，2＝﹣1+m，
∴m＝3；
（2）过点B作BC∥x轴（自己完成）交直线y2＝﹣x+3于点C．
设B点的纵坐标为n，则B（，n），C（3﹣n，n），
∵BC＝2，
∴3﹣n﹣＝2，
解得n＝，
∴B（，），
故答案为（，）．

22．（10分）某花农要将规格相同的800棵平安树运往A，B，C三地销售，要求运往C地的棵数是运往A地棵数的3倍，各地的运费如表所示：

A地
B地
C地
运费（元/棵）
10
20
15
（1）设运往A地的平安树x（棵），总运费为y（元）试写出y与x的函数关系式；
（2）若要求运往A地的平安树不超过运往B地的平安树，且总运费不超过14000元，问当运往A地的平安树多少棵时，总运费才最省？
【分析】（1）先分别求出运往B，C两地的棵数，根据总运费＝运往A地的费用+运往B地的费用+运往C地的费用，由条件就可以列出解析式；
（2）先根据题干信息求出x的取值范围，再利用一次函数的性质即可求解．
【解答】解：（1）运往A地的平安树x棵，则运往C地3x棵，运往B地（800﹣4x）棵，由题意得
y＝10x+20（800﹣4x）+15×3x，
y＝﹣25x+16000．
∵800﹣4x＞0且x＞0，
∴0＜x＜200，
故y与x的函数关系式为：y＝﹣25x+16000（0＜x＜200，x为整数）；
（2）由题意得：
，
解得：80≤x≤160，
由一次函数的性质可知：在80≤x≤160范围内，y随x的增大而减小，
∴x＝160时，y有最小值．
答：当运往A地的平安树160棵时，总运费才最省．
23．（12分）已知，在▱ABCD中，AE⊥BC于点E，AF⊥CD于点F，且AE＝AF．
（1）如图1，当EC＝4，AE＝8时，求▱ABCD的对角线BD的长；
（2）如图2，若点M为CD的中点，连接EM，AM．求证：AM＝EM．

【分析】（1）先根据平行四边形的性质、三角形全等的判定定理可得AB＝AD，再根据菱形的判定可得四边形ABCD是菱形，然后利用勾股定理分别求出BC、AC的长，最后利用等面积法即可得解；
（2）如图，先根据三角形全等的判定定理与性质可得AM＝FM，再根据直角三角形斜边上的中线等于斜边的一半即可得证．
【解答】解：（1）连接AC，如图，

∵四边形ABCD是平行四边形，
∴∠ABE＝∠ADF，
在△ABE和△ADF中，，
∴△ABE≌△ADF（AAS），
∴AB＝AD，
∴平行四边形ABCD是菱形，
∴AB＝BC，AC⊥BD，
∵EC＝4，AE＝8，AE⊥BC，
∴，
设AB＝BC＝x，则BE＝BC﹣EC＝x﹣4，
在Rt△ABE中，AE2+BE2＝AB2，则82+（x﹣4）2＝x2，
解得，x＝10，即AB＝BC＝10，
∴，
∴，
解得，BD＝8；
（2）如图，延长AM、EC交于点F，

∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠D＝∠FCM，∠DAM＝∠F，
∵点M为CD的中点，
∴DM＝CM，
在△ADM和△FCM中，，
∴△ADM≌△FCM（AAS），
∴AM＝FM＝，
∴EM是Rt△AEF斜边AF上的中线，
∴，
即AM＝EM．