数学5.2 函数的基本性质教学ppt课件

这是一份数学5.2 函数的基本性质教学ppt课件，共25页。PPT课件主要包含了艾宾浩斯记忆遗忘曲线，函数在R上是增函数，x12，x22，例2利用定义等内容，欢迎下载使用。

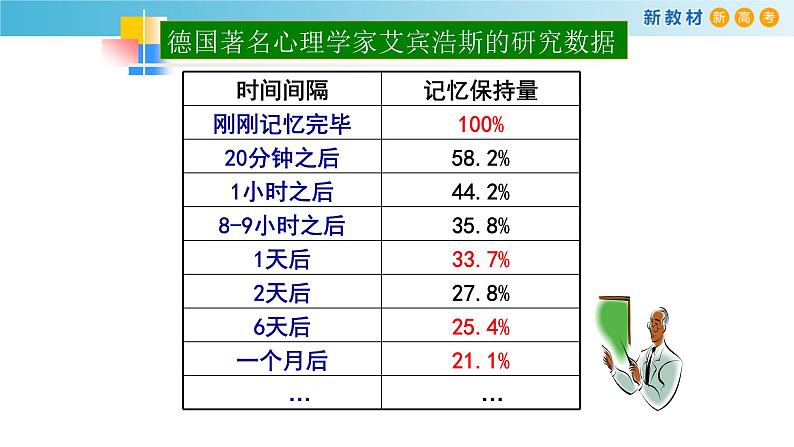
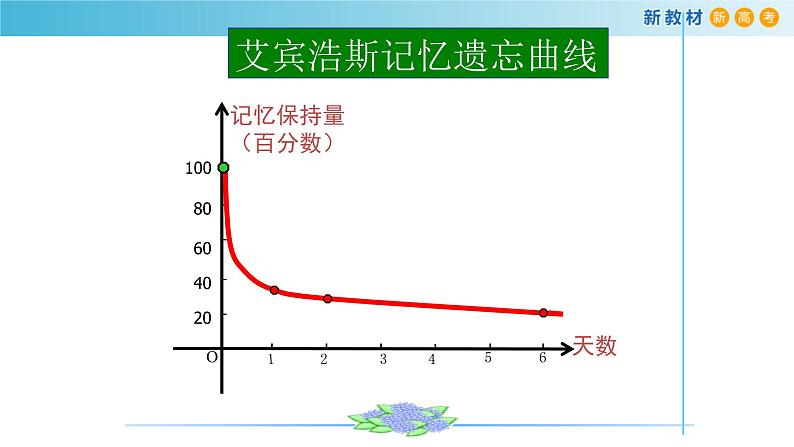
德国著名心理学家艾宾浩斯的研究数据
总结函数的变化规律：有的函数在定义域上是随着自变量的增大而增大；有的函数在定义域上是随着自变量的增大而减小；有的函数在定义域内的部分区间上是随着自变量的增大而增大或减小。问题：怎样准确描述这种变化规律？
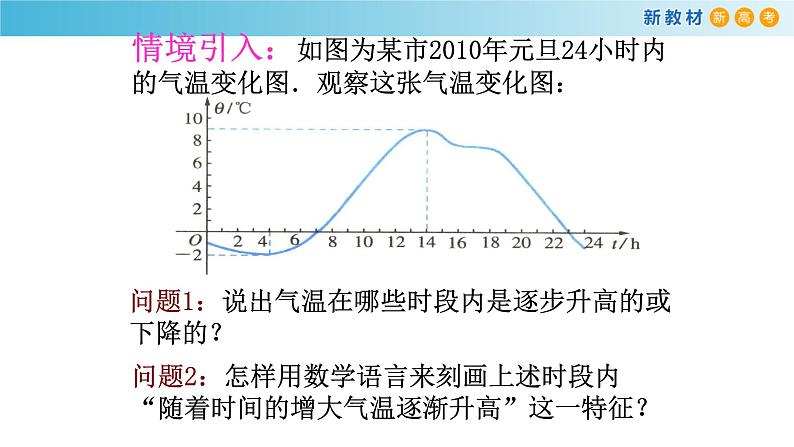
情境引入：如图为某市2010年元旦24小时内的气温变化图．观察这张气温变化图：
问题1：说出气温在哪些时段内是逐步升高的或下降的？
问题2：怎样用数学语言来刻画上述时段内“随着时间的增大气温逐渐升高”这一特征？
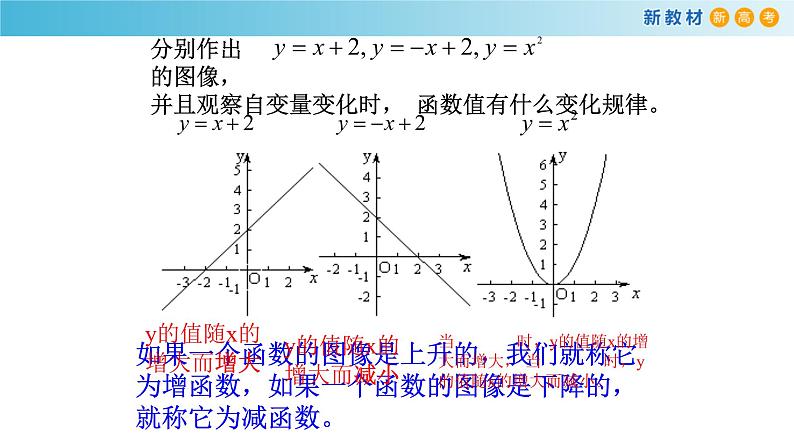
如果一个函数的图像是上升的，我们就称它为增函数，如果一个函数的图像是下降的，就称它为减函数。
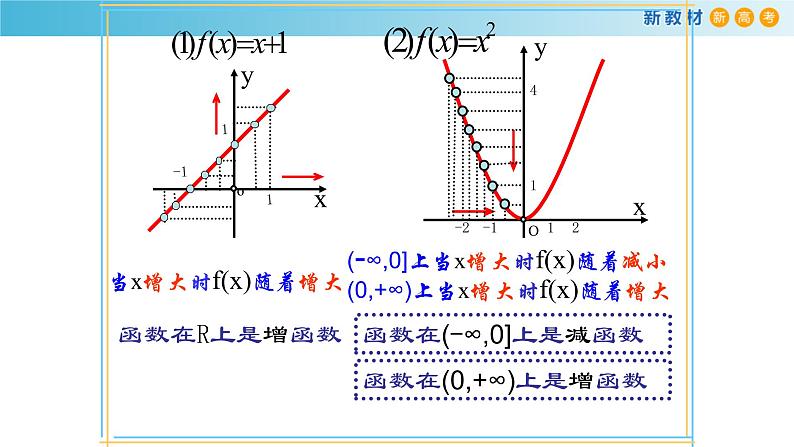
观察下列函数的图象，回答当自变量 的值增大时,函数值 是如何变化的？
(-∞,0]上当x增大时f(x)随着减小
当x增大时f(x)随着增大
函数在(-∞,0]上是减函数
(0,+∞)上当x增大时f(x)随着增大
函数在(0,+∞)上是增函数
 函数 f(x)=x2 :
在(0,+∞)上任取 x1、x2 ,
一般地，设函数 f(x)的定义域为A:
在(-∞,0)上是____函数
在(0,+∞)上是____函数
反比例函数 ：
在 (0,+∞) 上任取 x1、 x2 当x1< x2时，都有f(x1) f(x2)
取自变量－1< 1， 而 f(－1) f(1)
如果函数y=f(x)在区间M上是增函数或减函数，那么就说函数y=f(x)在这一区间上具有单调性，区间M叫做函数f(x)的单调区间.
(1)函数的单调性是相对于某一区间而言的性质，不能笼统的说某一函数是单调函数。(2)判断函数的单调性，应对所给区间内的任意两个值 、 来考察对应的函数值 与 的大小，而不能取特殊值。(3)单调区间必须写成区间的形式，当端点在其定义域上时，可以包括端点，也可以不包括端点.
解:函数y=f(x)的单调区间有[－5,－2）,[－2,1) ，[1，3), [3，5].
例1. 如图是定义在闭区间[－5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数？
其中y=f(x)在区间[－2，1)，[3，5]上是增函数；
说明:孤立的点没有单调性,故区间端点处若有定义写开写闭均可.
证明函数　　　 在R上是减函数.
4.下结论:由定义得出函数的单调性.
1.设值:设任意x1、x2属于给定区间,且x1< x2则△x= x2 -x1>0时
2.作差变形:作差△y=f(x2)-f(x1)并适当变形；
3.判断差符号:确定△y的正负；
证明函数单调性的步骤：
能否根据 的符号判断函数单调性
当 时，函数在M上是增函数 当 时，函数在M上是减函数
证明：设x1,x2 是(0,+∞)任意两个不相等的实数，且 x1练习.1.证明函数f(x)=2 x2 +1在(0,+∞)上是增函数。
2.下图是定义在区间[-5，5]上的函数y=f(x)，根据图象说出函数的单调区间，以及在每个区间上,它是增函数还是减函数？
解:函数y=f(x)的单调区间有
其中y=f(x)在区间[-5, -2), [1, 3)上是减函数， 在区间[-2, 1), [3, 5] 上是增函数.
[-5, -2), [-2,1), [1, 3), [3, 5].
3.画出下列函数图像，并写出单调区间：
讨论1：根据函数单调性的定义，
单调区间的书写原则：1.首先考虑定义域2.相同的单调区间一般不能写成并集，只能用逗号连接。3.若函数在区间端点处有定义，则写成闭区间，当然写成开区间也可以，若函数在区间端点处无定义，则必须写成开区间。
3.(定义法)证明函数单调性的步骤:
2.图象法判断函数的单调性：
1. 增函数、减函数的定义；