




高中数学上教版(2020)必修 第一册5.1 函数授课课件ppt
展开知识点 函数的三种表示方法1.函数的三种表示方法
2.三种表示方法的优缺点比较
【诊断分析】 任何一个函数都可以用解析法、列表法、图像法三种形式表示吗?
解:不一定.例如,函数的对应关系是:当x为有理数时,函数值等于1,当x为无理数时,函数值等于0.此函数就无法用图像法表示.
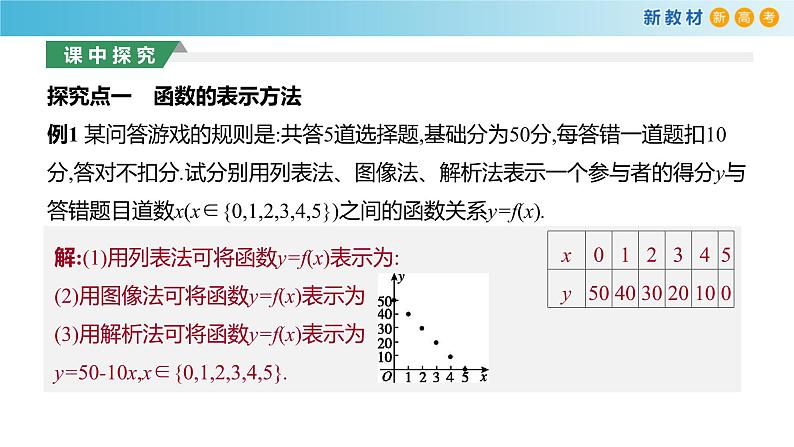
探究点一 函数的表示方法例1 某问答游戏的规则是:共答5道选择题,基础分为50分,每答错一道题扣10分,答对不扣分.试分别用列表法、图像法、解析法表示一个参与者的得分y与答错题目道数x(x∈{0,1,2,3,4,5})之间的函数关系y=f(x).
解:(1)用列表法可将函数y=f(x)表示为:(2)用图像法可将函数y=f(x)表示为(3)用解析法可将函数y=f(x)表示为y=50-10x,x∈{0,1,2,3,4,5}.
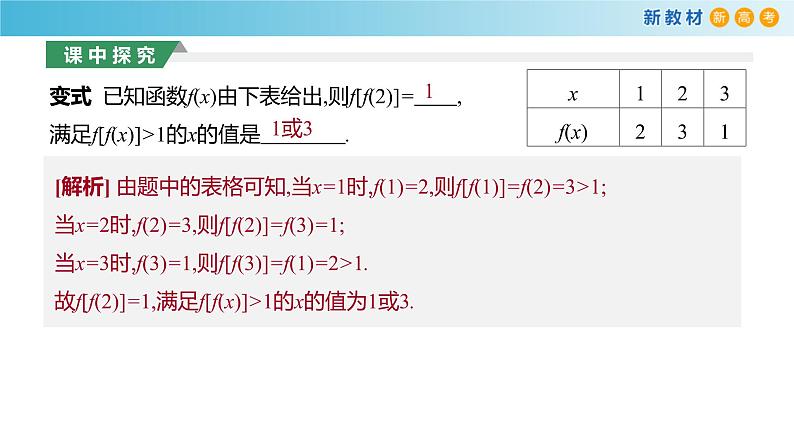
变式 已知函数f(x)由下表给出,则f[f(2)]= ,满足f[f(x)]>1的x的值是 .
[解析] 由题中的表格可知,当x=1时,f(1)=2,则f[f(1)]=f(2)=3>1;当x=2时,f(2)=3,则f[f(2)]=f(3)=1;当x=3时,f(3)=1,则f[f(3)]=f(1)=2>1.故f[f(2)]=1,满足f[f(x)]>1的x的值为1或3.
解:列表:描点,连线,如图所示,其图像是直线y=2x+1的一部分,观察图像可知,其值域为[1,5].
(3)y=x2+2x,x∈[-2,2].
描点、连线,如图所示,其图像是抛物线y=x2+2x的一部分.由图可得该函数的值域是[-1,8].
变式 小明用篱笆围出一块周长为12 m的矩形空地做生物试验,已知矩形的一边长为x(单位:m),面积为y(单位:m2).求y关于x的函数表达式,写出自变量x的取值范围并画出函数图像.
[素养小结]一般地,作函数图像时分以下三个步骤:(1)列表.先找出一些有代表性的自变量x的值,并计算出与这些自变量相对应的函数值f(x),用表格的形式表示出来.(2)描点.把第(1)步表格中的点(x,f(x))一一在坐标平面上描出来.(3)连线.用平滑的曲线把这些点按自变量由小到大的顺序连接起来.
拓展 电讯资费调整后,市话费标准为:通话时间不超过3分钟收费0.2元;超过3分钟后,每增加1分钟收费0.1元,不足1分钟按1分钟计费.通话收费S(元)与通话时间t(分钟)的函数图像可表示为( )
A B C D图5-2-1
[解析] 由题意知,当0
拓展 (1)已知af(x)+f(-x)=bx,其中a≠±1,求f(x);
1.待定系数法已知函数解析式的类型求其解析式时,通常利用待定系数法求解.
[例] 设二次函数f(x)的图像关于直线x=2对称,且f(x)=0的两实根的平方和为10,f(x)的图像过点(0,3),求f(x)的解析式.
2.函数与方程法在已知函数关系中含有可以对称代换的式子时,常用解方程组法求其解析式.
[例] 若3f(x)+2f(-x)=2x,求f(x).
解:由已知 3f(x)+2f(-x)=2x①,得3f(-x)+2f(x)=-2x②,联立①②消去f(-x)得,f(x)=2x.
1.已知函数f(x)由下表给出,则f(3)等于( )A.-1 B.-2 C.-3 D.-4
2.“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则图5-2-2中的图像与故事情节相吻合的是( )
A B C D图5-2-2
[解析] 由于兔子中间睡了一觉,所以有一段路程不变,而乌龟的路程在到达终点之前始终在增加,且乌龟比兔子早到终点,故选B.
3.函数f(x)=kx+1的图像不经过第三象限,则k的取值范围是( )A.k>0 B.k≥0C.k<0 D.k≤0
[解析] 当k<0时,函数图像经过第一、二、四象限;当k=0时,函数图像经过第一、二象限;当k>0时,函数图像经过第一、二、三象限,不合题意.故选D.
5.已知f(x)是一次函数,且满足3f(x+1)=6x+4,则f(x)= .
补充 区间表示法
区间表示法
必修 第一册4.1 幂函数说课课件ppt: 这是一份必修 第一册4.1 幂函数说课课件ppt,共27页。PPT课件主要包含了幂函数的图像,的图像,证明幂函数的增减性,答案A,当堂检测,答案D等内容,欢迎下载使用。
数学必修 第一册4.2 指数函数课文课件ppt: 这是一份数学必修 第一册4.2 指数函数课文课件ppt,共20页。PPT课件主要包含了整体感知,新知探究,增函数,减函数,发现该城市人口经过,归纳小结,目标检测等内容,欢迎下载使用。
高中数学上教版(2020)必修 第一册4.3 对数函数优秀课件ppt: 这是一份高中数学上教版(2020)必修 第一册4.3 对数函数优秀课件ppt,共34页。PPT课件主要包含了学习目标,作图步骤,问题探究,关于x轴对称,0+∞,对数函数的图象和性质,记忆口诀,对数函数单调性的应用,∵a21,∵3485等内容,欢迎下载使用。













