上教版（2020）必修 第一册4.3 对数函数公开课ppt课件

这是一份上教版（2020）必修 第一册4.3 对数函数公开课ppt课件，共21页。PPT课件主要包含了情境导入，知识海洋，0＋∞，应用探究，达标检测等内容，欢迎下载使用。

回忆：什么是指数函数？
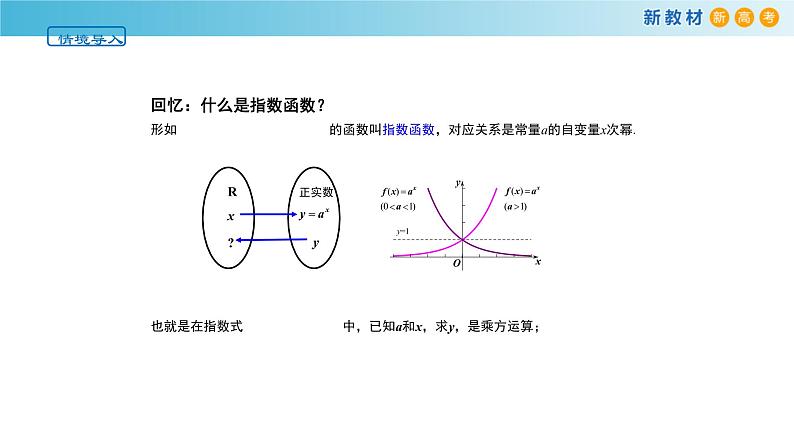
形如 的函数叫指数函数，对应关系是常量a的自变量x次幂.
也就是在指数式 中，已知a和x，求y，是乘方运算；
根据函数定义，这是以y为自变量，x为因变量的函数.
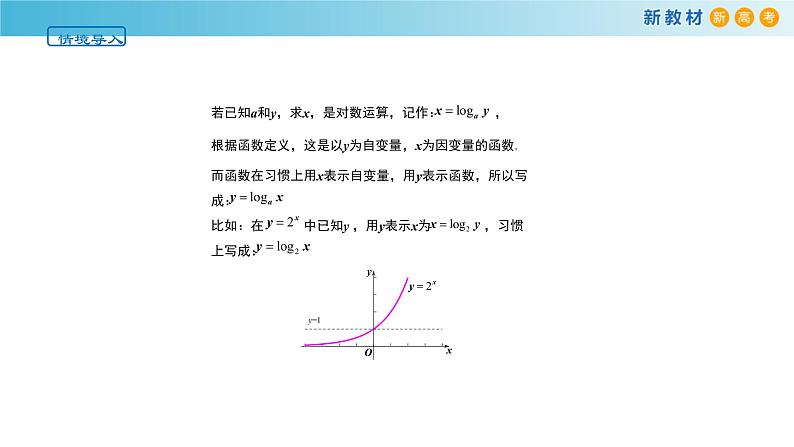
而函数在习惯上用x表示自变量，用y表示函数，所以写成：
比如：在 中已知y ，用y表示x为 ，习惯上写成：
定义：一般地，形如 的函数叫对数函数.
当生物死亡后，它机体内原有的碳14会按确定的规律衰减，大约每经过5730年衰减为原来的一半，这个时间称为“半衰期”.按照上述变化规律，生物体内碳14含量y与死亡年数x之间有怎样的关系？
问题：已知死亡生物体内碳14含量y，如何得知它死亡了的年数x呢？
分析：由 得
过y轴正半轴上任意一点 作x轴的平行线，与 的图象有且只有一个交点 .这就说明，对于任意一个 ，通过对应关系 在 上都有唯一确定的数x和它对应，所以x也是y的函数.
刻画了死亡生物体死亡年数x随体内碳14含量衰减而变化的规律.
如：指数函数 ，相对应的对数函数为？ 答： 再比如 ，相对应的对数函数为？ 答： 再比如 ，相对应的对数函数为？ 答： 再比如 ，相对应的对数函数为？ 答：
知识点一　对数函数的概念
　一般地，把 叫做对数函数，其中x是自变量，函数的定义域是 .
函数y＝lgax(a>0，且a≠1)
知识点二　对数函数的图象
对数函数y＝lgax(a>0，且a≠1)的图象和性质如下表：
例1　求下列函数的定义域.(1)y＝lga(3－x)＋lga(3＋x)；
类型一　对数函数的定义域的应用
∴函数的定义域是{x|－3(2)y＝lg2(16－4x).
解　由16－4x>0，得4x<16＝42，由指数函数的单调性得x<2，∴函数y＝lg2(16－4x)的定义域为{x|x<2}.
即－3所以－1(2)y＝lg(x＋1)(16－4x)；
如，求 定义域时，若先变形，则有
注：求定义域时，不要对所求解析式进行变形.
此时，得到的定义域为{x|x>0}.显然，这是错误的.
解　(1)先画出函数y＝lg x的图象(如图1).(2)再画出函数y＝lg|x|的图象(如图2).(3)最后画出函数y＝lg|x－1|的图象(如图3).
例2　画出函数y＝lg|x－1|的图象.
类型二　对数函数的图象
跟踪训练2　画出函数y＝|lg(x－1)|的图象.
解　(1)先画出函数y＝lg x的图象(如图1).(2)再画出函数y＝lg(x－1)的图象(如图2).(3)再画出函数y＝|lg(x－1)|的图象(如图3).
1.下列函数为对数函数的是A.y＝lgax＋1(a＞0且a≠1)B.y＝lga(2x)(a＞0且a≠1)C.y＝lg(a－1)x(a＞1且a≠2)D.y＝2lgax(a＞0且a≠1)
2.函数y＝lg2(x－2)的定义域是A.(0，＋∞) B.(1，＋∞)C.(2，＋∞) D.[4，＋∞)