高中数学上教版（2020）必修 第一册4.3 对数函数优秀课件ppt

这是一份高中数学上教版（2020）必修 第一册4.3 对数函数优秀课件ppt，共34页。PPT课件主要包含了学习目标，作图步骤，问题探究，关于x轴对称，0+∞，对数函数的图象和性质，记忆口诀，对数函数单调性的应用，∵a21，∵3485等内容，欢迎下载使用。
1.通过具体对数函数图像，掌握对数函数的图像和性质 特征，并能解决问题。2.知道同底的对数函数与指数函数互为逆运算。
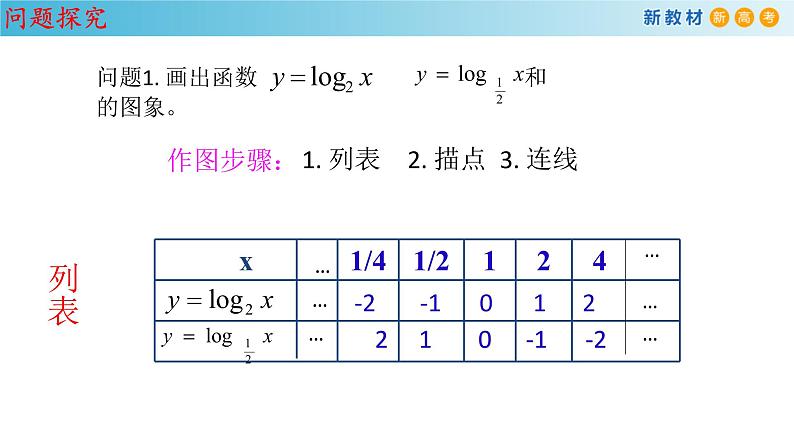
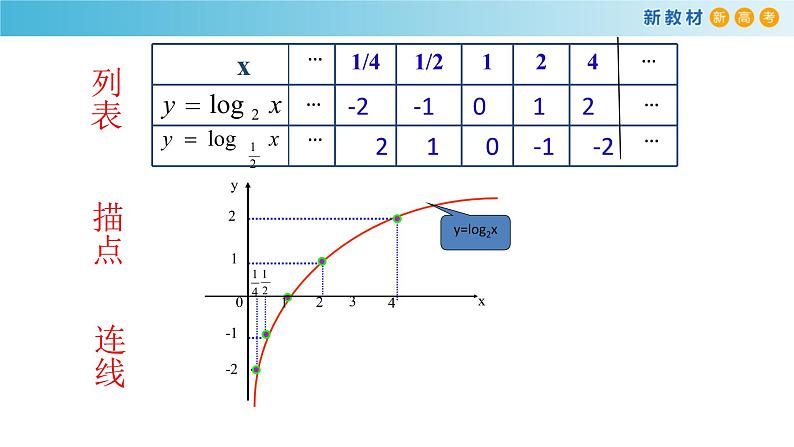
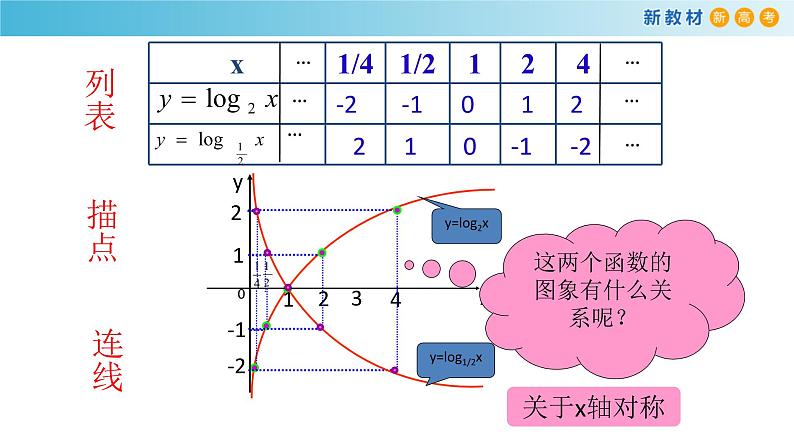
2 1 0 -1 -2
-2 -1 0 1 2
1. 列表 2. 描点 3. 连线
-2 -1 0 1 2
2 1 0 -1 -2
这两个函数的图象有什么关系呢？
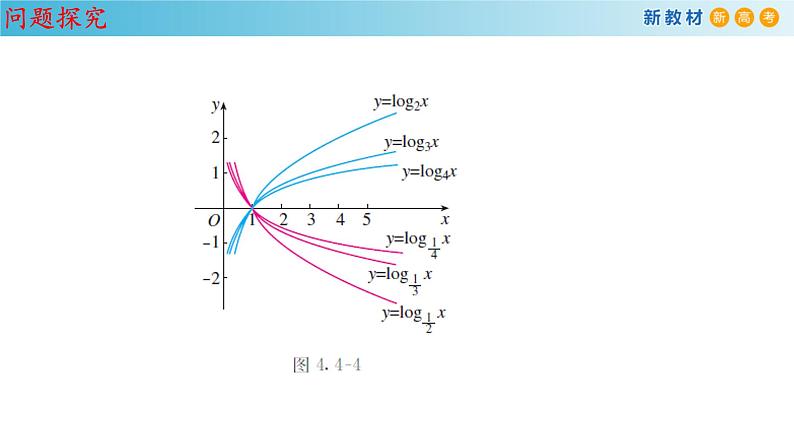
y=lgax（a>1）的图象
y=lgax（0 0;当 0 < x < 1 时， y < 0.
当 x > 1 时，y < 0;当 0 < x < 1 时， y > 0.
对数函数的性质的助记口诀:
对数增减有思路, 函数图象看底数;底数只能大于0, 等于1来也不行;底数若是大于1, 图象从下往上增;底数0到1之间, 图象从上往下减;无论函数增和减, 图象都过(1,0)点.
命题角度1　比较同底对数值的大小例　比较下列各组数中两个值的大小.(1)lg23.4，lg28.5；
解　考察对数函数y＝lg2x，因为它的底数2>1，所以它在(0，＋∞)上是增函数，又3.4＜8.5，于是lg23.41时，y＝lgax在(0，＋∞)上是增函数，又5.1＜5.9，于是lga5.11.∵y＝lg2x在(0，＋∞)上单调递增，∴lg2(3x＋1)>lg21＝0.即f(x)的值域为(0，＋∞).
跟踪训练3　已知f(x)＝lg2(1－x)＋lg2(x＋3)，求f(x)的定义域、值城.
f(x)＝lg2[(1－x)(x＋3)]＝lg2[－(x＋1)2＋4].∵x∈(－3,1)，∴－(x＋1)2＋4∈(0,4].∴lg2[－(x＋1)2＋4]∈(－∞，2].即f(x)的值域为(－∞，2].
练习1: 比较下列各题中两个值的大小: ⑴ lg106 lg108 ⑵ lg0.56 lg0.54 ⑶ lg0.10.5 lg0.10.6 ⑷ lg1.51.6 lg1.51.4
练习2：已知下列不等式，比较正数m，n 的大小： (1) lg 3 m < lg 3 n (2) lg 0.3 m > lg 0.3 n (3) lg a m < lga n (01)
对数函数y=lg a x (a>0, a≠1)
指数函数y=ax (a>0,a≠1)
(4) a>1时, x