鲁教版 (五四制)八年级上册第四章 图形的平移与旋转综合与测试习题课件ppt

这是一份鲁教版 (五四制)八年级上册第四章 图形的平移与旋转综合与测试习题课件ppt，共35页。PPT课件主要包含了答案呈现，习题链接等内容，欢迎下载使用。
分析下面给出的五种运动是否属于平移．(1)急刹车的汽车在地面上的运动；(2)沿直线行驶的汽车的运动；(3)时钟分针的运动；(4)高层建筑的电梯的运动；(5)小球从高处向下坠落(球不转动)． 
方法总结：判断物体是否做平移运动的方法：看变化前后各对应部分移动的方向是否相同，移动的距离是否相等，物体的大小和形状是否发生变化．
(1)急刹车的汽车在地面上的运动；(2)沿直线行驶的汽车的运动；
解：是平移，符合平移的定义和特征．
是平移，沿一定的方向移动，且形状、大小均未改变．
(3)时钟分针的运动；(4)高层建筑的电梯的运动；(5)小球从高处向下坠落(球不转动)． 
解：不是平移，不是沿一定方向移动一定的距离．
是平移，是上下平移的．
是平移，是向下平移的．
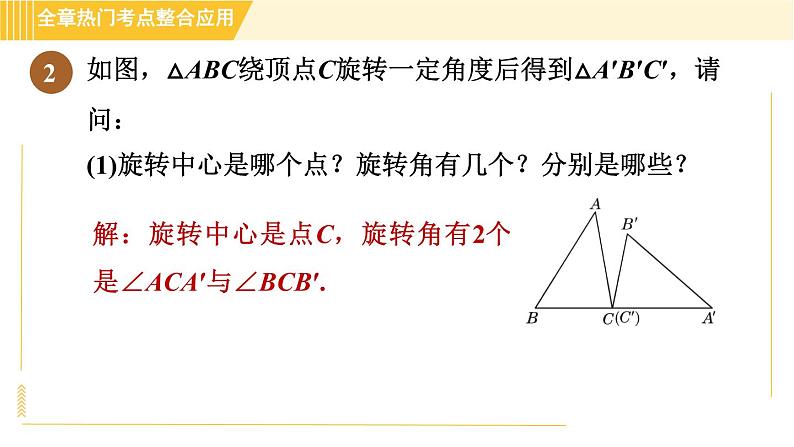
如图，△ABC绕顶点C旋转一定角度后得到△A′B′C′，请问：(1)旋转中心是哪个点？旋转角有几个？分别是哪些？
解：旋转中心是点C，旋转角有2个，分别是∠ACA′与∠BCB′.
解：点A到达点A′，点B到达点B′.
(2)经过旋转后，点A，B分别到达什么位置？(3)∠ACB′是否为旋转角？为什么？
∠ACB′不是旋转角，原因是在这个旋转过程中，线段CA与CB′不是对应边，因此线段CA与CB′所形成的角不是旋转角．
如图，如果甲、乙关于点O成中心对称，那么乙图中不符合题意的一块是(　　)
下列图形中，既是轴对称图形，又是中心对称图形的是(　　)
如图，已知△ABC的面积为36，将△ABC沿BC方向平移得到△A′B′C′，点B′和点C重合，连接AC′交A′C于点D.(1)求证：A′D＝CD；
证明：∵△ABC沿BC方向平移得到△A′B′C′，∴A′C′∥AC，A′C′＝AC，∴∠C′A′D＝∠ACD，又∵∠C′DA′＝∠ADC，∴△C′A′D≌△ACD，∴A′D＝CD.
(2)求△C′DC的面积．
如图，点O是等边三角形ABC内一点，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD.已知∠AOB＝110°.(1)求证：△COD是等边三角形；
证明：由旋转的性质得CO＝CD，∠OCD＝60°，∴△COD是等边三角形．
解：当α＝150°时，△AOD是直角三角形．理由：由旋转的性质得△BOC≌△ADC，∴∠ADC＝∠BOC＝150°.∵△COD是等边三角形，∴∠ODC＝60°，∴∠ADO＝90°，即△AOD是直角三角形．
(2)当α＝150°时，试判断△AOD的形状，并说明理由；
(3)探究：当α为多少度时，△AOD是等腰三角形？
解：∵△COD是等边三角形，∴∠COD＝60°.①当AO＝AD时，∠AOD＝∠ADO.∵∠AOD＝360°－∠AOB－∠COD－∠BOC＝360°－110°－60°－α＝190°－α，∠ADO＝∠ADC－∠CDO＝α－60°，∴190°－α＝α－60°，∴α＝125°；
②当OA＝OD时，∠OAD＝∠ADO，∵∠AOD＝190°－α，∠ADO＝α－60°，∴∠OAD＝180°－(∠AOD＋∠ADO)＝50°，∴α－60°＝50°，∴α＝110°；③当OD＝AD时，∠OAD＝∠AOD，即190°－α＝50°，∴α＝140°.综上所述，当α为125°，110°或140°时，△AOD是等腰三角形．
如图，在一块平行四边形的菜地中，有一口圆形的水井，现在张大爷要在菜地上修建一条笔直的小路将菜地面积二等分以播种不同的蔬菜，且要使水井在小路上，以便有利于对两块地进行浇灌，请你帮助张大爷画出小路修建的位置．
【点拨】平行四边形和圆都是中心对称图形，根据中心对称图形的性质，小路的位置应在平行四边形的对称中心A和圆的对称中心B的连线上．
解：如图，小路应修建在直线AB上．
利用如图所示的“基本图形”，经过旋转设计一个你喜欢的图案．
【点拨】本题答案不唯一，只要是由已知的“基本图形”旋转而成的图案均可．
解：将“基本图形”绕着点O按顺时针方向旋转45°七次，便可得到一个美丽的图案，如图所示．
如图，在六边形ABCDEF中，已知AB∥DE，AF∥CD，BC∥FE，AB＝DE，AF＝CD，BC＝FE，FD⊥BD，FD＝24 cm，BD＝18 cm，你能求出六边形ABCDEF的面积吗？
【点拨】平移体现了图形与图形之间的一种变换关系，有时为了把分散的条件集中起来，常利用图形的平移变换．平移变换可以开阔思路，化难为易．
解：能．如图，将△DEF竖直向上平移，使点D与点B重合，点E与点A重合，得到△BAG，将△BCD水平向左平移，使点D与点F重合，点C与点A重合，得到△GAF，则△DEF≌△BAG，△BCD≌△GAF，GB∥FD，GF∥BD.∴S△DEF＝S△BAG，S△BCD＝S△GAF.又∵FD⊥BD，∴S六边形ABCDEF＝S△DEF＋S△BCD＋S四边形BDFA＝S△BAG＋S△GAF＋S四边形BDFA＝S四边形BDFG＝FD·BD＝24×18＝432(cm2)．
证明：∵AD平分∠BAC，∴∠BAE＝∠CAE.∵BE⊥AD，∴把△ABE沿AD翻折得到△AFE，如图，
课外兴趣小组活动时，老师提出了如下问题：如图①，在△ABC中，若AB＝5，AC＝3，求BC边上的中线AD的取值范围．小明在经过组内合作交流后，得到了如下的解决方法：将△ACD绕点D逆时针旋转180°得到△EBD，从而把AB，AC，2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4.
根据上述解题过程，请你回答下列问题：如图②，在△ABC中，D是BC的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF.(1)求证：BE＋CF＞EF；
证明：如图，把△CFD绕点D逆时针旋转180°后得到△BGD，连接EG，由已知得，F，D，G三点共线，CF＝BG，DF＝DG.∵DE⊥DF，∴EF＝EG.在△BEG中，BE＋BG＞EG，即BE＋CF＞EF.
(2)若∠A＝90°，探索线段BE，CF，EF之间的等量关系，并加以证明．
解：BE2＋CF2＝EF2.证明：辅助线作法同(1)．由(1)知，F，D，G三点共线，CF＝BG，EG＝EF.∵∠A＝90°，∴∠EBC＋∠FCB＝90°，由中心对称的性质知，△CDF≌△BDG，∴∠FCD＝∠DBG，∴∠EBC＋∠DBG＝90°，即∠EBG＝90°，∴在Rt△EBG中，BE2＋BG2＝EG2，又∵EF＝EG，BG＝FC，∴BE2＋CF2＝EF2.
如图，P是正方形ABCD的边CD上一点，∠BAP的平分线交边BC于点Q，求证：AP＝DP＋BQ.
【点拨】将△ABQ旋转到△ADE的位置，将线段的和DP＋BQ表示成一条线段PE，再证明PE＝AP.
证明：如图，将△ABQ绕点A逆时针旋转90°后得到△ADE.∴∠EAQ＝90°，△AED≌△AQB.∴∠E＝∠AQB，DE＝BQ，∠ADE＝∠B＝90°.∴E，D，P三点共线．又∵∠BAP的平分线交边BC于点Q，AD∥BC，∴∠BAQ＝∠PAQ，∠DAQ＝∠AQB.∴∠PAE＝90°－∠PAQ＝90°－∠BAQ＝∠DAQ＝∠AQB＝∠E.∴AP＝PE＝DP＋DE＝DP＋BQ.
如图，在平面直角坐标系中，将△ABC向右平移3个单位长度后得到△A1B1C1，再将△A1B1C1绕点O旋转180°后得到△A2B2C2，则下列说法正确的是(　　)